SFTF is incorrect
https://github.com/braton/fadapt/blob/master/ls/rls/SFTF.m is not correct and is the same as the https://github.com/braton/fadapt/blob/master/ls/rls/FTF.m . They are both unstabilized Fast Transversal.
I had a look at the code from the book you mention and his example ( chapter 14 partA.m ) his code only works for real signals and I don't know how to extend that to complex signals.
The stability am currently looking at seems to be due to quantization error. It's perfectly stable and well-behaved up until about 15,000 samples then all of a sudden it explodes and the numbers get huge. In real life tests I have also seen numbers getting incredibly small in absolute magnitude but I haven't looked into that.
I know QR, lattice and I assume all the sliding window versions are stable. QR is too expensive. Lattice I haven't figured out how to use because I am using blind adaption and I need the equalized value before I can tell you the desired value; it might be possible but I don't really know how a lattice description of the filter works. I was excited with sliding window fast array and seemed to be great in Matlab but when converting it over to C++ and trying it out in a real-life example it was terrible; so that's a no go. Fast Transversal works really well in real life but it's instability is a problem.
I have adapted your https://github.com/braton/fadapt/blob/master/ls/rls/FTF.m for blind constant modulus adaption.
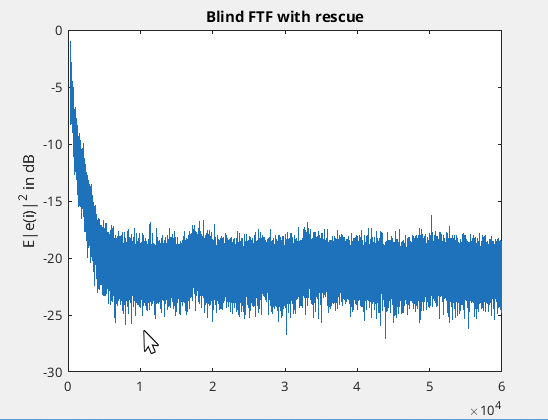
The code from the book you mention using the rescue mechanism for FTF doesn't make sense for complex numbers so I'm not quite sure how to extend it to complex numbers. However with a bit of modification I seem to be able to get it to rescue before blows up. I'm not sure it's always going to work or whether it will fail in real life but in Matlab code it seems to be working so far. Here is the code with some simulation testing...
close all
clear all
%number of trials for smoothing
nTrials=30;
%length of signal
uLen=60000;
%channel noise
SNR = 20;
%channel
channel=zeros(64,1);
channel(round(numel(channel)/2))=1;
channel(numel(channel))=0.6+1i*0.2;
%create on air signal
var_v = 10^(-SNR/10);
signal_sent = (2*randi(2,uLen,1)-3).'+1i*(2*randi(2,uLen,1)-3).';
channel_noise = sqrt(var_v)*randn(1,uLen)+1i*sqrt(var_v)*randn(1,uLen);
signal_received=filter(channel,1,signal_sent+channel_noise);
%received signal
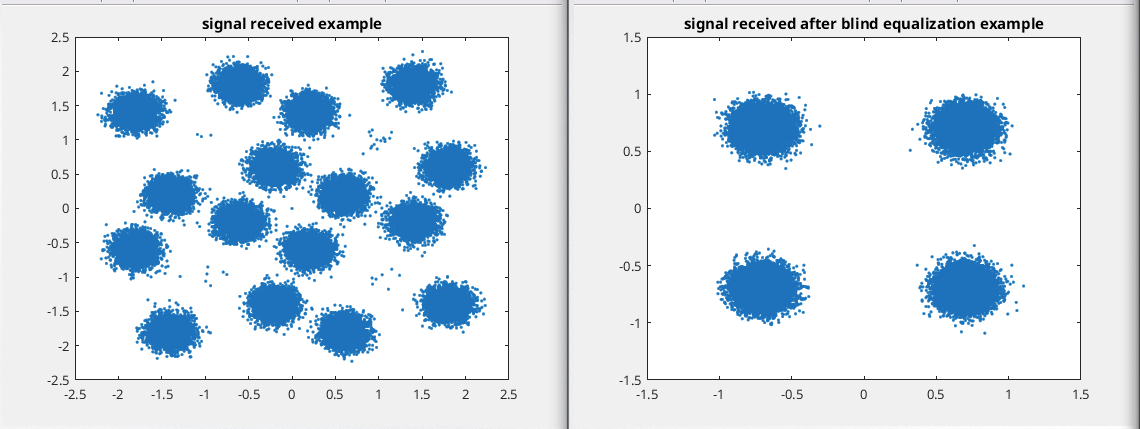
plot(signal_received,'.');
title('signal received example');
%run through some trials so we can smooth the output
learn_modifiedFTF=zeros(1,numel(signal_received));
for k=1:nTrials
disp(['trial ' num2str(k) ' of ' num2str(nTrials)] );
%create on air signal
var_v = 10^(-SNR/10);
signal_sent = (2*randi(2,uLen,1)-3).'+1i*(2*randi(2,uLen,1)-3).';
channel_noise = sqrt(var_v)*randn(1,uLen)+1i*sqrt(var_v)*randn(1,uLen);
signal_received=filter(channel,1,signal_sent+channel_noise);
%blind equalize
[w,y,errors]=modifiedFTF(signal_received,0.998,333,512);
learn_modifiedFTF = learn_modifiedFTF + abs(errors).^2;
end
%plot learning
learn_modifiedFTF = 10*log10(learn_modifiedFTF/nTrials);
figure;
plot(learn_modifiedFTF);
ylabel('E|e(i)|^2 in dB');
title('Blind FTF with rescue');
%plot some of a equalized signal
figure;
plot(y(6000:end),'.');
title('signal received after blind equalization example');
%FTF filter with I think rescue but not the stable version in the book.
%uses blind equalization and complex input.
%the book's code can't deal with complex signal and I don't know how to
%change to complex. I only understand RLS enough to be dangerous.
function [w,y,errors] = modifiedFTF( u,a,e,N )
% Initialization ----------------------------------------------------------
w=zeros(N,1);
uLen = length(u);
y = zeros(1,uLen);
uN = zeros(1,N);
wfpos = zeros(N,1);
wb = zeros(N,1);
gamma = 1;
rfpos = e*a^-2;
cNe = zeros(N+1,1);
rb = e*a^(-N-2);
wfpri = zeros(N,1);
errors = zeros(1,uLen);
%w(1)=1;%latest tap. only past used
w(round(N/2))=1;%center tap. both past and future used
% Filtering ---------------------------------------------------------------
for i=1:uLen
fpri = u(i)-uN*wfpri;
fpos = gamma*fpri;
rfpri = a*rfpos+fpri'*fpos;
gamma = gamma*a*rfpos/rfpri;
wfpri = wfpos+fpos*cNe(1:N);
cNe = [0;cNe(1:N)]+(fpri'/(a*rfpos))*[1;-wfpos];
bpri = a*rb*cNe(N+1)';
%check if things are falling apart
%the book in clearly for real numbers so I'm not sure how to extend for
%complex numbers. 1.0 fails some times. 0.05 so far I haven't seen fail
if (abs(bpri*gamma*cNe(N+1)')>0.05)
ind = num2str(i);
str = ['rescue used at iteration ',ind];
disp(str) % message
%reset most things but not the filter taps
gamma = 1;
cNe = 0*cNe;
wb = 0*wb;
wfpri = 0*wfpri;
rfpri = e*a^-2;
rb = e*a^(-N-2);
else
gamma = gamma/(1-bpri*gamma*cNe(N+1));
cNe = cNe-cNe(N+1)*[-wb;1];
bpos = gamma*bpri;
rb = a*rb+bpri'*bpos;
wb = wb+bpos*cNe(1:N);
end
uN = [u(i),uN(1:N-1)];%slide a new input in
y(i) = uN*w;%calc the point based on the filter
%either adapt to constant modulus or if you have carrier lock then go
%for the directed decision
if(abs(y(i))>0.00001)
d=y(i)/abs(y(i));%CM
%d=(sign(real(y(i)))+1i*sign(imag(y(i))))/sqrt(2);%needs carrier
else
d=y(i);
end
errors(i)=(d-y(i));%for user info
epos = gamma*(d-y(i));
w = w+epos*cNe(1:N);
wfpos = wfpri;
rfpos = rfpri;
end
end
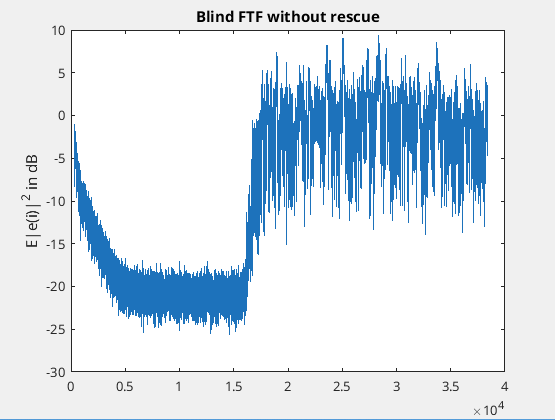
But yes without stabilization most of these RTL filters all fail around 15,000 to 20,000 samples. Interesting but frustrating.
Cheers, Jonti
nope I tried a bigger test of 50 trials and at least one failed to rescue the filter using if (abs(bpri*gamma*cNe(N+1)')>0.05)
Hello Jonti,
It's been quite a while when I looked at these algorithms for the last time.
I checked and indeed the SFTF implementation posted here is the the same as FTF. This is definitely a mistake.
Unfortunately I don't have time right now to dive into that again. I just mention one thing. Did you try the BEFAP algorithms (https://github.com/braton/fadapt/tree/master/misc) to check if it fits your needs?
It's a fast implementation of e-APA (https://github.com/braton/fadapt/blob/master/stoch/eAPA.m) called FAP (Fast Affine Projection). The computational complexity is further reduced by implementing it in a block manner (and providing correction to the output signal that takes into account the block computation). The original paper it was based on is here: http://www.tara.tsukuba.ac.jp/~maki/reprint/Tanaka/ma99sap79-86.pdf
It's also described in my Master thesis (https://github.com/braton/fadapt/blob/master/cner.pdf) at page 55 (unfortunately it's in polish).
I remember having very good stability and speed of convergence with this algorithm. It combines speed of least squares algorithms with stability of stochastic gradient algorithms. Maybe it will help.
Best Regards, Bartosz Zator
P.S. Someday I will rewrite it in Python (with NumPy) but it's not that day yet.
Hi Bartosz,
Yes it's tricky looking at things ones done a long time ago. You went through a lot of very different algos; I'm impressed by how many of them you implemented.
I had a quick look at the BEFAP algorithms and both of them I seem to be unable to get y before d so I can't modify them into a blind algos.
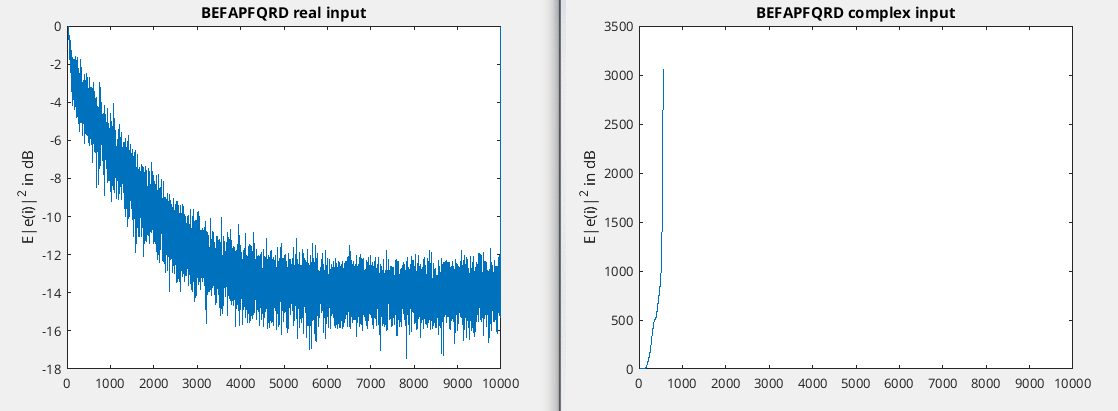
I also had a little bit further look into BEFAP_FQRD.m and it seems to be only able to deal with real input as you can see in the following figures with the code I used to produce the figures (I've added the modified FTF figures for reference)...
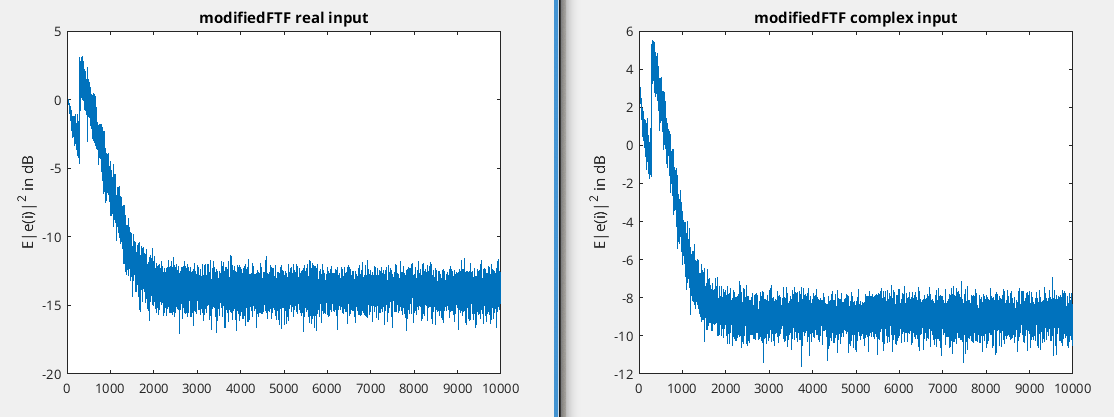
close all
clear all
%number of trials for smoothing
nTrials=40;
%length of signal
uLen=10000;
%channel noise
SNR = 150;
%channel
channel=zeros(64,1);
channel(round(numel(channel)/2))=1;
channel_delay=channel;
channel(numel(channel))=0.6+1i*0.2;
channel(16)=-0.16+1i*0.12;
learn_modifiedBEFAP_FQRD_real=zeros(1,uLen);
learn_modifiedBEFAP_FQRD_complex=zeros(1,uLen);
learn_modifiedFTF_real=zeros(1,uLen);
learn_modifiedFTF_complex=zeros(1,uLen);
for k=1:nTrials
disp(['trial ' num2str(k) ' of ' num2str(nTrials)] );
%create on air real signal
use_complex_signal=0;
var_v = 10^(-SNR/10);
signal_sent = (2*randi(2,uLen,1)-3).'+use_complex_signal*1i*(2*randi(2,uLen,1)-3).';
channel_noise = sqrt(var_v)*randn(1,uLen)+use_complex_signal*1i*sqrt(var_v)*randn(1,uLen);
signal_received=filter(real(channel)+use_complex_signal*1i*imag(channel),1,signal_sent+channel_noise);
desired_signal=filter(channel_delay,1,signal_sent);
% [y] = BEFAP_FQRD( u,d,m,e,p,L,N )
%
% u - Input signal;
% d - desired signal;
% m - stepsize;
% e - regularization factor;
% p - projection order;
% L - block length;
% N - filter order.
[y] = BEFAP_FQRD(signal_received,desired_signal,1.0,333/2,8,64,512 );
learn_modifiedBEFAP_FQRD_real = learn_modifiedBEFAP_FQRD_real + abs(y-desired_signal).^2;
%modified FTF with real
[y] = modifiedFTF(signal_received,desired_signal,0.998,333,512);
learn_modifiedFTF_real = learn_modifiedFTF_real + abs(y-desired_signal).^2;
%create on air complex signal
use_complex_signal=1;
var_v = 10^(-SNR/10);
signal_sent = (2*randi(2,uLen,1)-3).'+use_complex_signal*1i*(2*randi(2,uLen,1)-3).';
channel_noise = sqrt(var_v)*randn(1,uLen)+use_complex_signal*1i*sqrt(var_v)*randn(1,uLen);
signal_received=filter(real(channel)+use_complex_signal*1i*imag(channel),1,signal_sent+channel_noise);
desired_signal=filter(channel_delay,1,signal_sent);
%BEFAP_FQRD seems to fail for complex input
[y] = BEFAP_FQRD(signal_received,desired_signal,1.0,333,8,64,512 );
learn_modifiedBEFAP_FQRD_complex = learn_modifiedBEFAP_FQRD_complex + abs(y-desired_signal).^2;
%modified FTF with complex
[y] = modifiedFTF(signal_received,desired_signal,0.998,333,512);
learn_modifiedFTF_complex = learn_modifiedFTF_complex + abs(y-desired_signal).^2;
end
%plot learning
learn_modifiedBEFAP_FQRD_real = 10*log10(learn_modifiedBEFAP_FQRD_real/nTrials);
learn_modifiedBEFAP_FQRD_complex = 10*log10(learn_modifiedBEFAP_FQRD_complex/nTrials);
learn_modifiedFTF_real = 10*log10(learn_modifiedFTF_real/nTrials);
learn_modifiedFTF_complex = 10*log10(learn_modifiedFTF_complex/nTrials);
figure;
plot(learn_modifiedBEFAP_FQRD_real);
ylabel('E|e(i)|^2 in dB');
title('BEFAPFQRD real input');
figure;
plot(learn_modifiedBEFAP_FQRD_complex);
ylabel('E|e(i)|^2 in dB');
title('BEFAPFQRD complex input');
figure;
plot(learn_modifiedFTF_real);
ylabel('E|e(i)|^2 in dB');
title('modifiedFTF real input');
figure;
plot(learn_modifiedFTF_complex);
ylabel('E|e(i)|^2 in dB');
title('modifiedFTF complex input');
function [y] = BEFAP_FQRD( u,d,s,e,p,L,N )
% BEFAP_FQRD - Block Exact Fast Affine Projection Algorithm
% with Fast Array Recursive Least Squares Lattice prediction
%
% [y] = BEFAP_FQRD( u,d,m,e,p,L,N )
%
% u - Input signal;
% d - desired signal;
% m - stepsize;
% e - regularization factor;
% p - projection order;
% L - block length;
% N - filter order.
%
% y - Output signal.
%
% Bartosz Zator
% August 2006
%
% -------------------------------------------------------------------------
% Initialization ----------------------------------------------------------
% -------------------------------------------------------------------------
uLen=length(u);y=zeros(1,uLen);w=zeros(N,1);
% FRLS section ------------------------------------------------------------
wfLd=zeros(p,1);wfLd(1)=sqrt(1/e);wbLd=zeros(p,1);wbLd(p)=sqrt(1/e);
Pfd=(sqrt(e^(-1))*ones(1,p));Pbdp=(sqrt(e^(-1))*ones(1,p));
qbd=(zeros(1,p));qfd=qbd;
bposdp=(zeros(1,p+1));bposup=bposdp;
gammaup=(ones(1,p+1));gammadp=gammaup;
Ggain=(zeros(p,1));Ggaini=Ggain;
% -------------------------------------------------------------------------
Pfu=(zeros(1,p));Pbup=Pfu;
qbu=(zeros(1,p));qfu=qbu;
bposd=(zeros(1,p+1));bposu=bposd;fposd=bposd;fposu=bposd;
gammad=(zeros(1,p+1));gammau=gammad;
cNf=rand(1,p);sNf=cNf;chNf=cNf;shNf=cNf;
% APA section -------------------------------------------------------------
ruu=zeros(L+p-2,1);ur=zeros(1,N+L+p-2);ul=zeros(1,N+L-1);
E=zeros(p+L-1,1);ei=zeros(p,1);gu=zeros(p-1,1);
% -------------------------------------------------------------------------
% Filtering ---------------------------------------------------------------
% -------------------------------------------------------------------------
for i=1:uLen
%if ~mod(i,1000), disp(i); end;
ul=[u(i),ul(1:N+L-2)];
if ~mod(i,L)
f2=fft([w.',zeros(1,L)]);f1=fft([0,fliplr(ul)]);
Y=real(ifft(f1.*f2));Y=flipud(Y(N+1:N+L)');
for r=i-L+1:i
% Forward and Backward Prediction -----------------------------
gammad(1)=(1);gammau(1)=(1);
bposd(1)=(r-N+1>0)*u(max(r-N+1,1));bposu(1)=u(r);
fposd(1)=(r-N+1>0)*u(max(r-N+1,1));fposu(1)=u(r);
%disp([(r-N+1>0)*u(max(r-N+1,1)),u(r)]);pause;
for m=1:p
%-------------------------------------------%
% Backward Update
Pbup(m)=Pbdp(m)/sqrt(1+Pbdp(m)^2*bposup(m)^2);
cNb=Pbup(m)/Pbdp(m);sNb=bposup(m)*Pbup(m);
qfu(m)=qfd(m)*cNb+fposu(m)*sNb;
fposu(m+1)=fposu(m)*cNb-qfd(m)*sNb;
% Backward Downdate
Pbdp(m)=Pbup(m)/sqrt(1-Pbup(m)^2*bposdp(m)^2);
chNb=Pbdp(m)/Pbup(m);shNb=bposdp(m)*Pbdp(m);
qfd(m)=qfu(m)*chNb-fposd(m)*shNb;
fposd(m+1)=fposd(m)*chNb-qfu(m)*shNb;
%-------------------------------------------%
% Forward Update
Pfu(m)=Pfd(m)/sqrt(1+Pfd(m)^2*fposu(m)^2);
cNf(m)=Pfu(m)/Pfd(m);sNf(m)=fposu(m)*Pfu(m);
qbu(m)=qbd(m)*cNf(m)+bposup(m)*sNf(m);
bposu(m+1)=bposup(m)*cNf(m)-qbd(m)*sNf(m);
gammau(m+1)=gammaup(m)*cNf(m);
% Forward Downdate
%Pfdp(m)=1/Pfd(m);
Pfd(m)=Pfu(m)/sqrt(1-Pfu(m)^2*fposd(m)^2);
chNf(m)=Pfd(m)/Pfu(m);shNf(m)=fposd(m)*Pfd(m);
qbd(m)=qbu(m)*chNf(m)-bposdp(m)*shNf(m);
bposd(m+1)=bposdp(m)*chNf(m)-qbu(m)*shNf(m);
gammad(m+1)=gammadp(m)*chNf(m);
%-------------------------------------------%
end%m=1:p
% Update coefficients -----------------------------------------
Pbusc=sqrt(1/Pbdp(p)^2+abs(bposu(p))^2);
Pbdsc=sqrt(Pbusc^2-abs(bposd(p))^2);
wfLu=wfLd*cNf(p)-[0;Ggain(1:p-1)]*sNf(p);
Ggain=[0;Ggain(1:p-1)]*cNf(p)+wfLd*sNf(p);
wbLu=wbLd*(Pbusc*Pbdp(p))-Ggain*(bposu(p)*Pbdp(p));
Ggain=Ggain*(Pbusc*Pbdp(p))-wbLd*(bposu(p)*Pbdp(p));
wfLd=[0;Ggaini(1:p-1)]*shNf(p)+wfLu*chNf(p);
Ggaini=[0;Ggaini(1:p-1)]*chNf(p)+wfLu*shNf(p);
wbLd=wbLu*(Pbdsc/Pbusc)+Ggaini*(bposd(p)/Pbusc);
Ggaini=Ggaini*(Pbdsc/Pbusc)-wbLu*(bposd(p)/Pbusc);
% Delay management --------------------------------------------
bposdp=bposd;bposup=bposu;gammaup=gammau;gammadp=gammad;
% Affine Projection -------------------------------------------
ruu=ruu+u(r)*ur(1:L+p-2)'-ur(N)*ur(N+1:N+L+p-2)';
ur=[u(r),ur(1:N+L+p-3)];
k=(mod(r,L)+(mod(r,L)==0)*L);
auxerr=d(r)-Y(L-k+1);
err=auxerr-E(1:k+p-2)'*ruu(1:k+p-2);
y(r)=d(r)-err;
ei=[d(r)-y(r);(1-s)*ei(1:p-1)];
Bi=wbLu*wbLu'*ei;
Fi=wfLu*wfLu'*ei;
gi=[0;(1-s)*gu]+Fi;
gu=gi(1:p-1)-Bi(1:p-1);
E=[0;E(1:L+p-2)]+[s*gi;zeros(L-1,1)];
end%for r=i-L+1:i
f1=fft([0,fliplr(ur(p:p+N+L-2))]);
f2=fft([E(p:p+L-1).',zeros(1,N)]);
wf=real(ifft(f1.*f2));
w=w+flipud(wf(L+1:L+N)');
end%if ~mod(i,L)
end%for i=1:uLen
end
%FTF filter with I think rescue but not the stable version in the book.
%the book's code can't deal with complex signal and I don't know how to
%change to complex. I only understand RLS enough to be dangerous.
function [y] = modifiedFTF( u,d,a,e,N )
% Initialization ----------------------------------------------------------
w=zeros(N,1);
uLen = length(u);
y = zeros(1,uLen);
uN = zeros(1,N);
wfpos = zeros(N,1);
wb = zeros(N,1);
gamma = 1;
rfpos = e*a^-2;
cNe = zeros(N+1,1);
rb = e*a^(-N-2);
wfpri = zeros(N,1);
errors = zeros(1,uLen);
%w(1)=1;%latest tap. only past used
w(round(N/2))=1;%center tap. both past and future used
% Filtering ---------------------------------------------------------------
for i=1:uLen
fpri = u(i)-uN*wfpri;
fpos = gamma*fpri;
rfpri = a*rfpos+fpri'*fpos;
gamma = gamma*a*rfpos/rfpri;
wfpri = wfpos+fpos*cNe(1:N);
cNe = [0;cNe(1:N)]+(fpri'/(a*rfpos))*[1;-wfpos];
bpri = a*rb*cNe(N+1)';
%check if things are falling apart
%the book in clearly for real numbers so I'm not sure how to extend for
%complex numbers. 1.0 fails some times. 0.025 so far I haven't seen fail
if (abs(bpri*gamma*cNe(N+1)')>0.025)
ind = num2str(i);
str = ['rescue used at iteration ',ind];
disp(str) % message
%reset most things but not the filter taps
gamma = 1;
cNe = 0*cNe;
wb = 0*wb;
wfpri = 0*wfpri;
rfpri = e*a^-2;
rb = e*a^(-N-2);
else
gamma = gamma/(1-bpri*gamma*cNe(N+1));
cNe = cNe-cNe(N+1)*[-wb;1];
bpos = gamma*bpri;
rb = a*rb+bpri'*bpos;
wb = wb+bpos*cNe(1:N);
end
uN = [u(i),uN(1:N-1)];%slide a new input in
y(i) = uN*w;%calc the point based on the filter
epos = gamma*(d(i)-y(i));
w = w+epos*cNe(1:N);
wfpos = wfpri;
rfpos = rfpri;
end
end
Just looking at real inputs BEFAP_FQRD algo seems to be slower but maybe I just haven't found good parameters yet.
eAPA.m seems a midway between LMS and RLS. With a small projection order I'm thinking it will behave more like LMS and with a large projection order it will be more like RLS. The eAPA.m could be made blind but the computational cost scares me. There is a nasty inverse and for big projection orders (p) the matrix to invert gets bigger. So I think only the BEFAP algorithms would be viable from a computational cost. But comparing eAPA.m with FTF it seems for a big enough p it might converge quicker than FTF. That's a bit odd as BEFAP_FQRD.m converged slower than FTF...
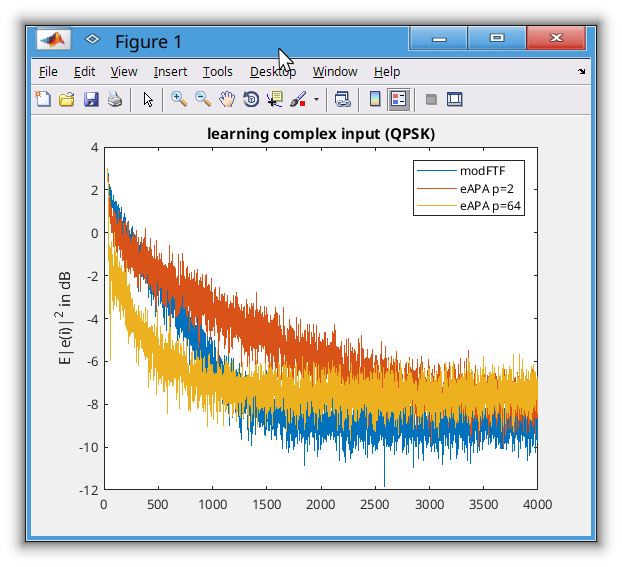
I haven't tested eAPA in real life so I could do that but the CPU cost might make it impractical. So far despite all FTF's instability FTF is still looking good. For now I keep trying to stabilize FTF and see how things go.
Cheers, Jonti
One last thing to mention, did you try FAP (Fast Affine Projection algorithm)? I haven't implemented that here but it's just a fast implementation of e-APA. BEFAP is just a FAP done in a block manner with delay, FAP shouldn't have this problem. So if e-APA would do the trick then FAP would also do the trick but significantly faster.
Hi Bartosz,
I had a quick look on the net for FAP and there seems to be a few versions. I looked at http://falbu.50webs.com/articole/gsfap_SIPS2002.pdf and that paper seems to say their GSFAP version is good. The paper is about echo cancellation so I realized that it might mean it not working for complex numbers but thought I'd give it a go as they supply matlab code which is nice. So I modified the code to make it more like yours and yup it only works for real numbers...
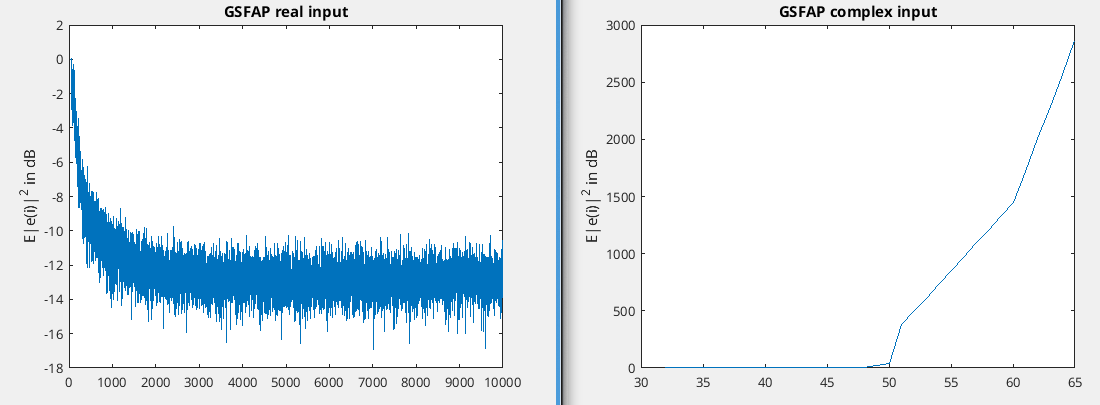
clear all
close all
%number of trials for smoothing
nTrials=40;
%length of signal
uLen=10000;
%channel noise
SNR = 150;
%channel
channel=zeros(64,1);
channel(round(numel(channel)/2))=1;
channel_delay=channel;
channel(numel(channel))=0.6+1i*0.2;
channel(16)=-0.16+1i*0.12;
learn_GSFAP_real=zeros(1,uLen);
learn_GSFAP_complex=zeros(1,uLen);
for k=1:nTrials
disp(['trial ' num2str(k) ' of ' num2str(nTrials)] );
%create real on air signal
use_complex_signal=0;
var_v = 10^(-SNR/10);
signal_sent = (2*randi(2,uLen,1)-3).'+use_complex_signal*1i*(2*randi(2,uLen,1)-3).';
channel_noise = sqrt(var_v)*randn(1,uLen)+use_complex_signal*1i*sqrt(var_v)*randn(1,uLen);
signal_received=filter(real(channel)+use_complex_signal*1i*imag(channel),1,signal_sent+channel_noise);
desired_signal=filter(channel_delay,1,signal_sent);
[y] = GSFAP(signal_received,desired_signal,1,10,32,10,512 );
learn_GSFAP_real = learn_GSFAP_real + abs(y-desired_signal).^2;
%create complex on air signal
use_complex_signal=1;
var_v = 10^(-SNR/10);
signal_sent = (2*randi(2,uLen,1)-3).'+use_complex_signal*1i*(2*randi(2,uLen,1)-3).';
channel_noise = sqrt(var_v)*randn(1,uLen)+use_complex_signal*1i*sqrt(var_v)*randn(1,uLen);
signal_received=filter(real(channel)+use_complex_signal*1i*imag(channel),1,signal_sent+channel_noise);
desired_signal=filter(channel_delay,1,signal_sent);
[y] = GSFAP(signal_received,desired_signal,1,10,32,10,512 );
learn_GSFAP_complex = learn_GSFAP_complex + abs(y-desired_signal).^2;
end
%plot learning
learn_GSFAP_real = 10*log10(learn_GSFAP_real/nTrials);
learn_GSFAP_complex = 10*log10(learn_GSFAP_complex/nTrials);
figure;
plot(learn_GSFAP_real);
ylabel('E|e(i)|^2 in dB');
title('GSFAP real input');
figure;
plot(learn_GSFAP_complex);
ylabel('E|e(i)|^2 in dB');
title('GSFAP complex input');
function [y] = GSFAP( u,d,mu,e,p,update_parameter,N )
% GAUSS-SEIDEL FAST AFFINE PROJECTION ALGORITHM
%
% u - Input signal;
% d - desired signal;
% mu - stepsize;
% e - regularization factor;
% p - projection order;
% update_parameter - update_parameter
% N - filter length.
%
% http://falbu.50webs.com/articole/gsfap_SIPS2002.pdf
% F. Albu, J. Kadlec, N. Coleman, A. Fagan, "The Gauss-Seidel Fast Affine Projection Algorithm", IEEE Workshop SIPS 2002, pp. 109-114, San Diego, U.S.A, October 2002
% Felix Albu
% Valahia University of Targoviste, Romania
% Email: [email protected]
% http://falbu.50webs.com
% initializations
u=u.';
d=d.';
uLen=numel(u);
V_matrix=zeros(p,1); %newest excitation vector
old_V=zeros(p,1); %oldest excitation vector
extended_V_matrix=zeros(N+p,1); % this contains p length N excitation vectors
neta_buf=zeros(p,1); % the E-vector in fap
W_aux_matrix=zeros(N,1); % the fap-adaptive filter auxiliary coefficients
y=zeros(1,uLen);
p_matrix=[1/e; zeros(p-1,1)];
b_vector=[1; zeros(p-1,1)];
rcorr_matrix = e * eye ( p, p );
rcorr_buf=[e;zeros(p-1,1)];
inv_vector=[1/e;zeros(p-1,1)];
for iter=1:uLen
% shift state vectors
V_matrix(2:p)=V_matrix(1:p-1);
V_matrix(1)=u(iter);
old_V(2:p)=old_V(1:p-1);
extended_V_matrix(2:N+p)=extended_V_matrix(1:N+p-1);
extended_V_matrix(1)=V_matrix(1);
old_V(1)=extended_V_matrix(N+1);
% update fap paramaters
rcorr_buf=rcorr_buf+V_matrix(1)*V_matrix(1:p)-old_V(1)*old_V(1:p);
rcorr_matrix(2:p,2:p)=rcorr_matrix(1:p-1,1:p-1);
rcorr_matrix(:,1)=rcorr_buf;
rcorr_matrix(1,:)=rcorr_buf';
inv_vector(2:p)=inv_vector(1:p-1);inv_vector(1)=1/rcorr_buf(1);
% GS section
if rem(iter,update_parameter)==0
for i=1:p
sum1=0;
for j=1:p
if j~=i
sum1=sum1-rcorr_matrix(i,j)*p_matrix(j);
end
end
p_matrix(i)=(b_vector(i)+sum1)*inv_vector(i);
end
end
W_aux_matrix=W_aux_matrix+mu*neta_buf(p)*extended_V_matrix(p+1:p+N);
y(iter)=extended_V_matrix(1:N)'*W_aux_matrix;
err_buf=d(iter)-y(iter);
err_buf=err_buf-mu*rcorr_buf(2:p)'*neta_buf(1:p-1);
epsilon_buf=err_buf*p_matrix;
neta_buf=[0; neta_buf(1:p-1)]+epsilon_buf;
end
end
It would be good for echo cancellation but the not working for complex numbers seems to be a reoccurring theme. I'll do a little more looking tomorrow.
Cheers, Jonti