TheAlgorithms
[FEATURE REQUEST] <Trapping Rain Water>
What would you like to Propose?
Problem Statement Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.
Example 1:
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6 Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
Example 2:
Input: height = [4,2,0,3,2,5] Output: 9
Constraints:
- n == height.length
- 1 <= n <= 2 * 104
- 0 <= height[i] <= 105
Issue details
Problem Statement Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.
Example 1:
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6 Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
Example 2:
Input: height = [4,2,0,3,2,5] Output: 9
Constraints:
- n == height.length
- 1 <= n <= 2 * 104
- 0 <= height[i] <= 105
Additional Information
No response
Approach To keep water, we have to have a bar on the left side and on the right side. Between them, we can keep water.
Let's think about this example.
Input: height = [2,1,0,1,3,2]
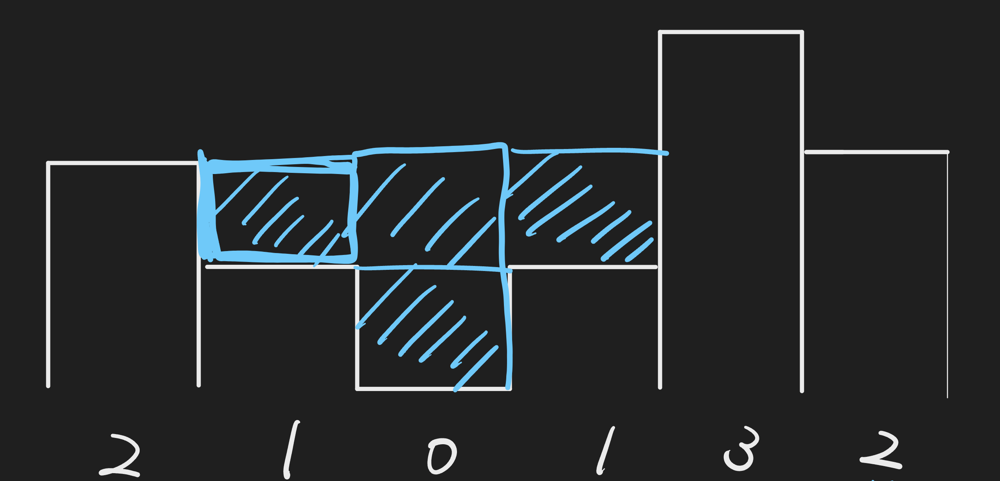I think we can easily imagine that we can keep water at 0 height(= index 2), because we have bars in the adjacent places(= index 1 and 3).
But how about 1 height at index 1. We can keep water there. I think left side is easy to imagine because we have a bar in adjacent place(= index 0). But how about right side? In the end, we can keep water because we have 3 height at index 4.
Question
How can we judge if we can have water when there is some distance between water and a bar? In this case, water is at index 1 and the bar is at index 4.
My strategy is to keep max height of left and right. I'll show you how algorithm works.
How it works
//Solution
[2,1,0,1,3,2] L R
left max = 2 right max = 2 water = 0
L is current left pointer. R is current right pointer. left max is max height of left side we found so far. Initialized with the first number. right max is max height of right side we found so far. Initialized with the last number water is return value.
If L is smaller than R, we continue. After that, check left max and right max and take smaller max height. I'll explain why later.
In this case, they are the same, so we can choose one of them. I'll take right.
First of all, move R to the next.
[2,1,0,1,3,2] L R
left max = 2 right max = 2 water = 0
Next, update right max if current bar is taller than current right max.
current bar vs current max right = 3 vs 2 = 3
[2,1,0,1,3,2] L R
left max = 2 right max = 3 water = 0
Then, count number of water. Formula is
water = current right max - current bar = 3 - 3 = 0
water should be 0. Next, L < R, so we continue
First of all, take smaller max height between left and right. I'll take left max.
Move L to the next and update left max if needed. No udpate this time.
[2,1,0,1,3,2] L R
left max = 2 right max = 3 water = 0
Then here is an important point. water should be
current left max - current bar 2 - 1 = 1
water = 1
⭐️ Points
We take smaller max height between left(= 2 height) and right(= 3 height) and handle left side because left max is smaller than right max. That means we don't have to care about right side because we know that we have current tallest bar(= 3 height at index 4) on the right side, so at least we can keep water at 2 height(= left max)
That's the reason why we take smaller max height.
We can take 2 height as max height but there is bar at index 1. That's why
left max - current height = 2 - 1 = 1 water
[2,1,0,1,3,2] L R
left max = 2 right max = 3 water = 1
L < R, so we continue. Move L to the next because left max is smaller than right max and update left max if needed. No update this time.
[2,1,0,1,3,2] L R
left max = 2 right max = 3 water = 1
water should be..
2 - 0 = 2 total water = 3
Next, L < R, so we continue. Move L to the next because left max is smaller than right max and update left max if needed. No update this time. [2,1,0,1,3,2] L R
left max = 2 right max = 3 water = 3
water should be...
2 - 1 = 1 total water = 4 Next, L < R, so we continue. Move L to the next because left max is smaller than right max and update left max if needed. we found 3 this time.
[2,1,0,1,3,2] L R left max = 3 (updated. 2 vs 3) right max = 3 water = 3 water should be...
3 - 3 = 0 total water = 4 Now L == R. We stop iteration.
return 4
Complexity
- Time complexity: O(n)
- Space complexity: O(1)
//Solution class Solution { public int trap(int[] height) { int left = 0, right = height.length - 1; int leftMax = height[0], rightMax = height[height.length - 1]; int water = 0; while (left < right) { if (leftMax < rightMax) { left++; if (leftMax < height[left]) { leftMax = height[left]; } else { water += leftMax - height[left]; } } else { right--; if (rightMax < height[right]) { rightMax = height[right]; } else { water += rightMax - height[right]; } } } return water; } }
//Solution
class Solution { public int trap(int[] height) { int left = 0, right = height.length - 1; int leftMax = height[0], rightMax = height[height.length - 1]; int water = 0; while (left < right) { if (leftMax < rightMax) { left++; if (leftMax < height[left]) { leftMax = height[left]; } else { water += leftMax - height[left]; } } else { right--; if (rightMax < height[right]) { rightMax = height[right]; } else { water += rightMax - height[right]; } } } return water; } }
