Implement the remaining methods of "ellipsoid" class in "GenEllipsoid" class
This includes polar, hpintersect and a few others - see issue #42 for more details
@pgagarinov Can you give me a small hint to generalize intersection algorithm of finite ellipsoid and hyper-plane described here (and implemented into elltoolboxcore+ellipsoid) on generalized case with infinite eigenvalues, please?
The same goes for polar() method
Regarding polar - please have a look at https://github.com/SystemAnalysisDpt-CMC-MSU/ellipsoids/issues/42#issuecomment-166861569 and talk to Alex Timchenko.
Regarding the intersection - the hint is that you need to use a definition of generalized ellipsoid (see comments for issue #46). Obviously an intersection of hyperplane and generalized ellipsoid is a generalized ellipsoid GE=E+L. So you need to find its E and L components separately. Start with a pen, a sheet of paper and a few simple 3-dimensional examples: unlimited cylinder, 2-dimensional ellipsoid in 3d space, 1-dimensional ellipsoid in 3d space. In each of the above examples figure out who an intersection looks like. This should help you with the formulas for n-dimensional case.
...
Some thoughts about implementation of polar: polar(E) = {l: \any x \in E (l, x) <= 1}
(l,x) can be decomposed as follows:
(l,x) = (l,x+dx) + (l,q) + (l,x_f) + (l,x_i) + (l,x_z)
where
q - center of E
dx=x-q
x_f - projection of dx on linear subspace L_f produced by eig. vectors with finite non-zero eig. values
x_i - projection of dx on linear subspace L_i produced by eig. vectors with infinite eig. values
x_z - projection of dx on linear subspace L_z produced by eig. vectors with zero eig. values
(L_f L_i and L_z are orthogonal and the decomposition is uniquely, of corse)
Using this decomposition we can note:
Intersection of ploar(E) with L_i must contain only origin
if l0 \in ploar(E) then l0 + l1 also in ploar(E) if l1 \in L_z
So, we know structure of the resulting set in L_z + L_i.
To know structure of polar set into L_f we can work inside L_f subspace and use regular formulas form
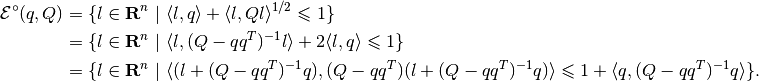 .
.
Before applying these formulas into L_f subspace we need firstly rotate ellipsoid and change ordering of eig. vectors. 'Finite' eigen vectors of transformed ellipsoid must be first and produce identity submatrix into matrix of eigen vectors.
After we can compute ploar set in transformed domain and recover it in original domain by using the formula
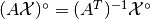 .
.
So, projection of ploar(E) on L_f computed we need only set zeros on diagonal of GenEllipsoid.diagMat in positions corresponding infinte eigen values, and set Inf values in positions corresponding to zero eig. values. Eig. vectors in L_i and L_z remain the same.