ConstantRateJump Differs from VariableRateJump with Constant Rate

[arnavs]

tl;dr Using a VariableRateJump with an actually constant jump rate differs (dramatically) from a ConstantRateJump with the same arrival function.

cc @ChrisRackauckas, @jlperla

Reproduction

The setup boilerplate you need for these two examples is at the bottom. That pretty much just defines the parameters, etc.

The key pieces are

rate_index(u, p, t, i) = 0.2 # constant across indices, times, etc.
affect_index!(integrator, index) = (integrator.u[index] = max(integrator.u[index], integrator.u[rand(1:integrator.p.N)])) 

So a constant rate and affect! structure for each problem.

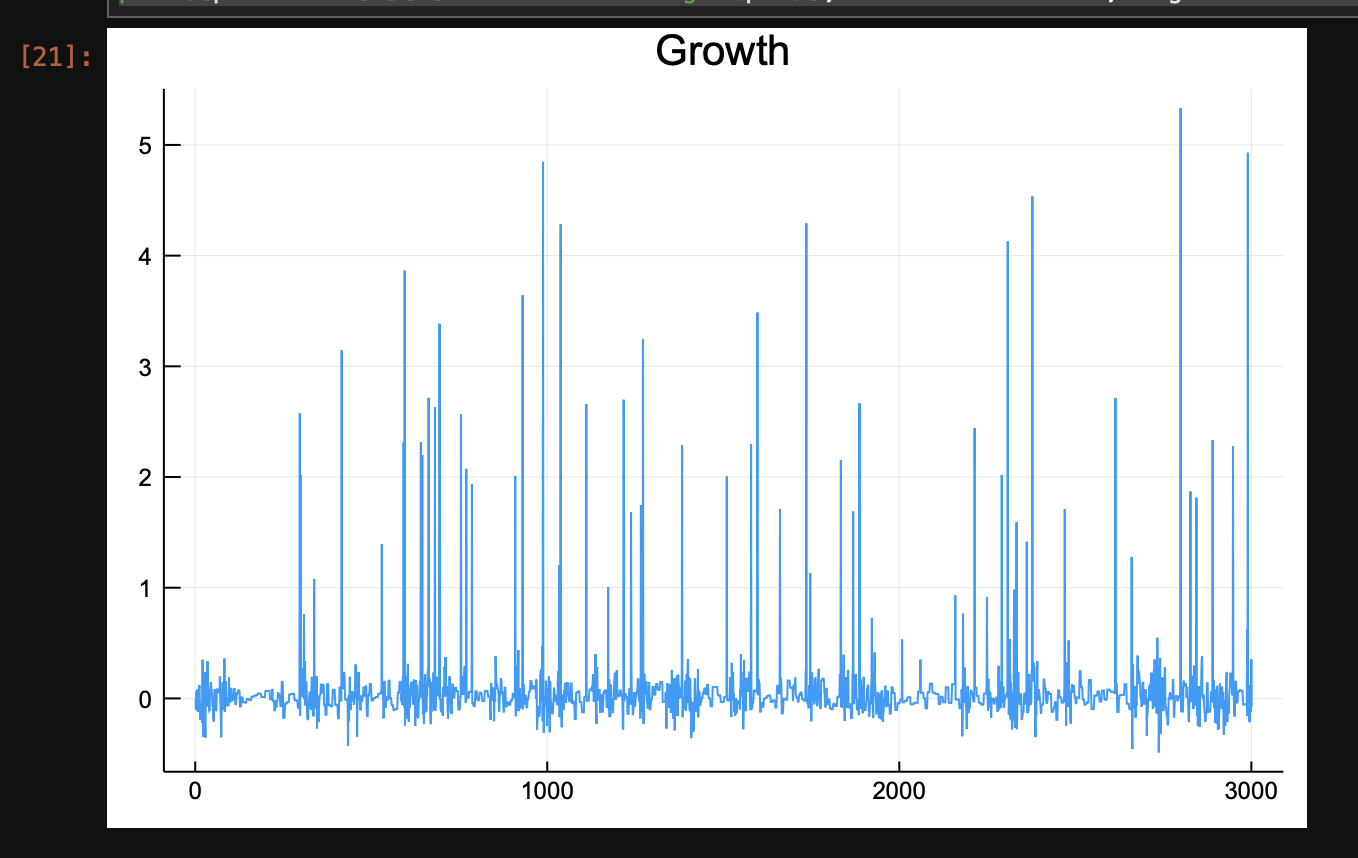
ConstantRateJump (Correct)

If I run

Random.seed!(1)
p = params()
sde_prob, cb = generate_sde_cb(p)
jumps = [ConstantRateJump((u, p, t) -> rate_index(u, p, t, i), (integrator) -> affect_index!(integrator, i)) for i in 1:p.N];
jump_prob = JumpProblem(sde_prob, DirectFW(), JumpSet((), jumps, nothing, nothing))
sim = solve(jump_prob, SRIW1(), callback = cb)
plot([p.moments[x][5] for x in 1:length(p.t)], title = "Growth", legend = false)

I see

Variable Rate

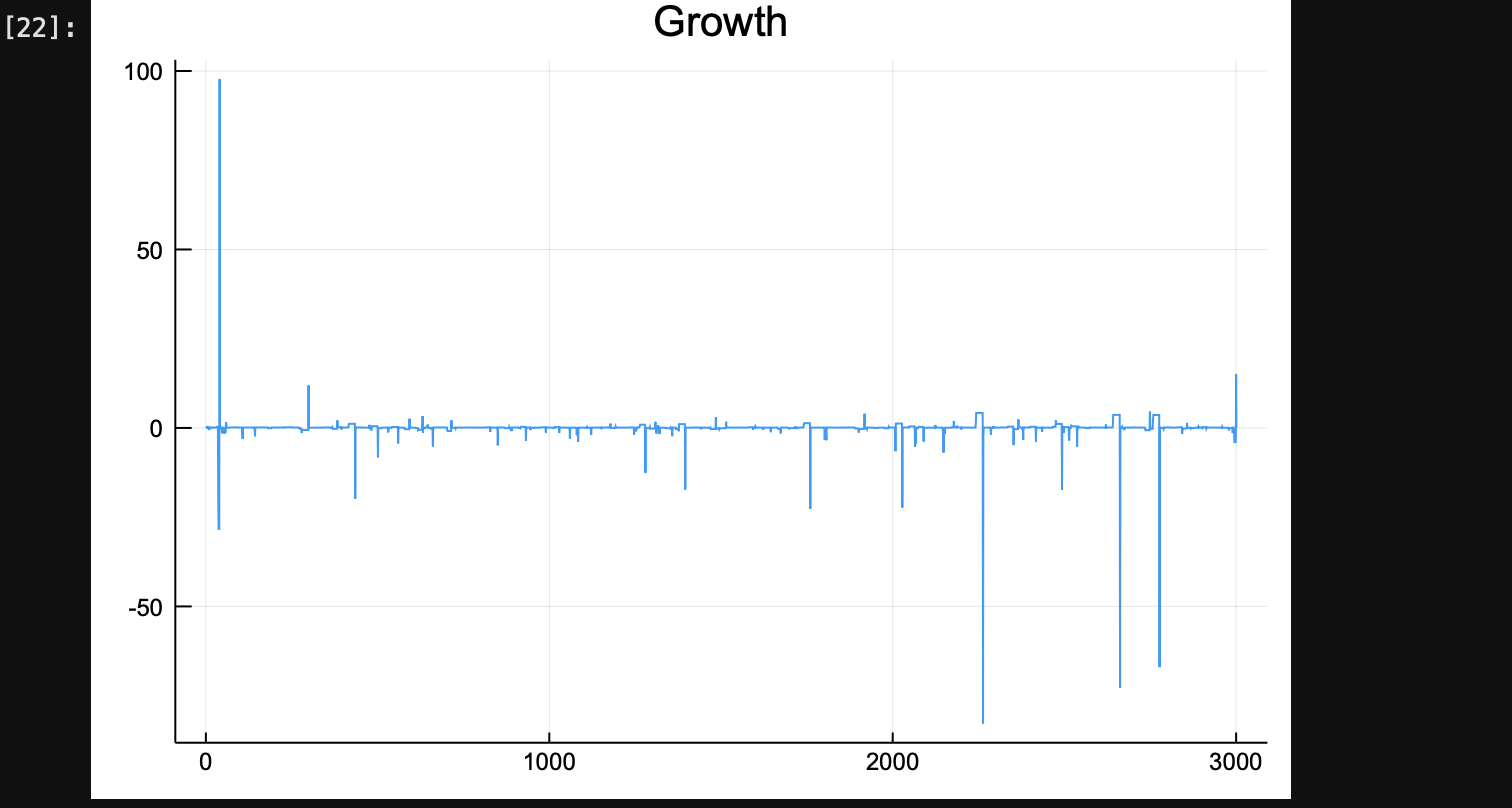
If I run

Random.seed!(1)
p = params()
sde_prob, cb = generate_sde_cb(p)
jumps = [VariableRateJump((u, p, t) -> rate_index(u, p, t, i), (integrator) -> affect_index!(integrator, i)) for i in 1:p.N];
jump_prob = JumpProblem(sde_prob, DirectFW(), JumpSet((jumps),(),nothing,nothing)) 
sim = solve(jump_prob, SRIW1(), callback = cb)
plot([p.moments[x][5] for x in 1:length(p.t)], title = "Growth", legend = false)

I see

Setup

First, run the following setup boilerplate that's common across the two examples.

using DiffEqJump, StochasticDiffEq, DiffEqCallbacks
using StatsBase, Parameters, Plots, Distributions, Random

# invariant parameters for each case
function drift(du,u,p,t) # constant drift
      du .= p.μ
end
function volatility(du,u,p,t) # constant shock exposure
      du .= p.σ
end

# main params bundle
params = @with_kw (
    μ = 0.01, # mean
    σ = 0.1, # drift
    N = 30, # num particles (==== 30 instead of 10 ====)
    β = 0.2, # rate parameter
    t = 0.:0.01:30., # time steps to save (==== 30 instead of 10 ====)
    moments = Array{Array{Float64, 1}, 1}(), # container for moments
    α = 2.0, # shape parameter for the initial condition distribution
    iv_dist = Exponential(1/α), # updates based on supplied α
    ρ_max = 2.0)

# boilerplate for all cases
function generate_sde_cb(p)
    x_iv = rand(p.iv_dist, p.N) # draw initial condition
    sde_prob = SDEProblem(drift, volatility, x_iv, (0.0, p.t[end]), p)
    function calculate_moments(u, t, integrator) 
        g = (length(integrator.p.moments) == 0. ? 0. : (mean(u) - integrator.p.moments[end][2])/step(integrator.p.t))
        moments = [minimum(u), mean(u), median(u), maximum(u), g]
        push!(integrator.p.moments, moments) 
    end
    cb = FunctionCallingCallback(calculate_moments; funcat=p.t, func_everystep=false, func_start = true, tdir=1)
    return sde_prob, cb
end

rate_index(u, p, t, i) = 0.2 # constant across indices, times, etc.
affect_index!(integrator, index) = (integrator.u[index] = max(integrator.u[index], integrator.u[rand(1:integrator.p.N)]))

[arnavs]

@ChrisRackauckas I know you said this will be a very difficult issue to fix, but is there some way you can flag it for the future?

I want to make sure that it isn't forgotten or dismissed as (e.g.) non-interesting, non-reproducible, etc.

[ChrisRackauckas]

The issue was confirmed to be event handling misses due to the large number of jumps. This was verified by checking jump_u for negatives. It's a hard issue to fix and I think we might need to change some things around to do it.