digraph_dijkstra_shortest_paths in case of equal weights of edges with equivalent source nodes

[Chipoki]

first of all - many thanks for putting the effort into this library. it truly is immensely faster than networkx, without being much less readable and modular.

for the issue/s I currently deal with -

In cases where my graph has multiple subsequent edges, originating from the same source node, with the same weights (lets say 0) - for some reason, when calculating a digraph_dijkstra_shortest_paths of the graph, a rather random (42, haha ;]) indexed edge is picked out, while any of those edges would have led to the same path lengths.

when I use networkx (as well as MATLAB's digraph's shortest_path function) the first edge is picked. this picking order effects my final result (since the nodes represent actual indices of some array in my program), and It seems there is no flag that would allow me to control this picking order and make the path use the first viable edge.

I did notice though - that this phenomenon is rather inconsistent (which probably points on my lack of understanding as to why this happens in the first place), since, from some point on - the first alternative is the one to be picked, and then suddenly the non-first alternative is picked again, etc.

another issue I've been dealing with is the fact that when I use 'extend_from_weighted_edge_list' on my PyDiGraph, it does not accept float typed weights, and requires them to also be integers. it would be nice if I could use my original fragmented weights instead of multiplying them by some large number in order to (partly) preserve their information.

my code looks like so:

    graph = rx.PyDiGraph(multigraph=False)
    in_out_weight_triplets = np.concatenate((in_node_indices, out_node_indices,
                                             np.abs(weights_matrix) * 100000), axis=1)
    graph.extend_from_weighted_edge_list(list(map(tuple, in_out_weight_triplets.astype(int))))
    shortest_path = rx.digraph_dijkstra_shortest_paths(graph, source=n_nodes, target=n_nodes + 1,
                                                       weight_fn=lambda x: x)

thanks in advance for any guidance\enhancement in the matter, and thanks again for making this library exist :)

[mtreinish]

For the question about extend_from_weighted_edge_list() floats are definitely allowed for the weight parameter in the input tuples. In fact there are no constraints placed on a edge (or node) weight and they can be any python object. However, node indices (which are the first 2 elements in the tuple) are required to be ints. For example, if you run

import retworkx as rx
graph = rx.PyDiGraph(multigraph=False)
graph..extend_from_weighted_edge_list([(0, 1, 3.2), (0, 2, 3.2), (0, 3, 3.2), (1, 4, 1.0), (2, 4, 1.0), (3, 4, 1.0)])

it generates a graph like:

I think the issue you're facing is that the first two elements in the tuples for extend_from_weighted_edge_list() aren't node weights but actually node indices. What extend_from_weighted_edge_list() does is add nodes with a weight None to the graph if there are any missing indices in the set of nodes in the graph. For example, if you ran:

import retworkx as rx
graph = rx.PyDiGraph(multigraph=False)
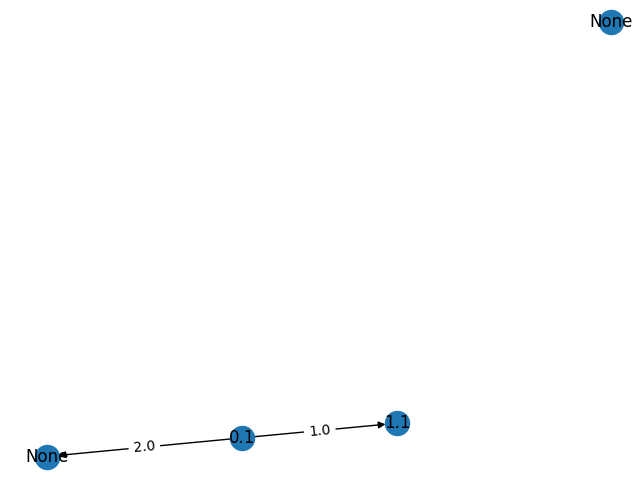
graph.add_nodes_from([0.1, 1.1])
graph.extend_from_weighted_edge_list([(0, 1, 1.0), (0, 3. 2.0)])

That will create a graph with 4 nodes with weights 0.1, 1.1, None, and None and edges between nodes with the weights 0.1 -> 1.1 and 0.1 and one of the nodes with weight None, while the other node create with weight None is not connected to any other node in the graph. This is created because the hole in the node index list: 2 is created by extend_from_weighted_edge_list():

For the question about dijkstra's algorithm I'm not sure I understand what the issue is and I'm not really able to reproduce any non-determinism in the behavior with a fixed graph input, even with parallel edges that have identical weights. I ran dijkstra on the graph generated in the above code snippet with:

import retworkx as rx
graph = rx.PyDiGraph(multigraph=False)
graph..extend_from_weighted_edge_list([(0, 1, 3.2), (0, 2, 3.2), (0, 3, 3.2), (1, 4, 1.0), (2, 4, 1.0), (3, 4, 1.0)])
shortest_path = rx.digraph_dijkstra_shortest_paths(graph, source=0, target=4, weight_fn=lambda x: x)
print(shortest_path)

which always returns PathMapping{4: [0, 3, 4]}

Dijkstra's algorithm should behave deterministically as you can see from the code:

https://github.com/Qiskit/retworkx/blob/0.10.2/src/shortest_path/dijkstra.rs#L100-L172

what might be confusing here though is that the node and edge indices aren't necessarily always in insertion order if there are any removals the removed indices are reused on subsequent additions. Also, the inner loop (which is this line: https://github.com/Qiskit/retworkx/blob/0.10.2/src/shortest_path/dijkstra.rs#L129 ) doesn't start with the first edge added on node but instead starts with the most recently inserted. Which means the path with the most recently inserted edge will be chosen assuming the rest of the edges in all the parallel paths have equal weights. This is why in the simple example above the path chosen is edges 2 and 5 instead of 0 and 3. Since in case of identical weights the most recently added edges will be selected first and none of the parallel edges will have a smaller weight.

The example code snippet in the issue body isn't actually a reproducible example and I can't actually run so I can't really give you any more targeted advice. If you can provide a more complete example of what you're running and an example of what is different from your expectations in that example hopefully we can get to the bottom of what's going wrong for you.