Hi there,

I am trying to create an optimized version of the correlation sum, a method that is used in nonlinear dynamics to estimate the dimension of fractal objects. The algorithm is in principle extremely simple and requires the calculation of the correlation sum

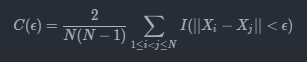
(where I = 1 if the condition is met, zero otherwise) for various values of ε. A simple but optimized Julia implementation is as follows

function correlationsum2(X, εs::AbstractVector, norm = Euclidean())
    d = distancematrix(X, norm)
    Cs = zeros(length(εs))
    N = length(X)
    @inbounds for (k, ε) in enumerate(εs)
        for i in 1:N
            @inbounds Cs[k] += count(d[j, i] < ε for j in i+1:N)
        end
    end
    return 2Cs ./ (N*(N-1))
end

function distancematrix(X, norm = Euclidean())
    N = length(X)
    return [evaluate(norm, X[i], X[j]) for i in 1:N, j in 1:N]
end

I've realized it might be possible to further enhance the speed of this thing using KDTrees, since in principle you only care about the points X[i] with distance < ε from X[j], i.e. its inrange neighbors.

I've made a working implementation with NearestNeighbors.jl through the Neighborhood.jl interface

function correlationsum(X, εs::AbstractVector, norm = Euclidean())
    tree = searchstructure(KDTree, X.data, norm)
    skip = Theiler(0)
    N = length(X)
    factor = 1/(N*(N-1))
    Cs = zeros(length(εs))
    # TODO: I seem to be missing an optimization step...
    @inbounds for (i, ε) in enumerate(εs)
        st = WithinRange(ε)
        idxs = bulkisearch(tree, X.data, st, skip)
        for j in 1:N
            Cs[i] += length(idxs[j])
        end
    end
    Cs .*= factor
    return Cs
end

where bulkisearch(tree, X.data, st, skip) is the "optimized" NearestNeighbors.jl method for finding all inrange neigbhors of all points in X.

Unfortunately, this method performs as well as the original distance-matrix based above but not better. I realized this might be because all neighboring indices idxs are allocated. It would be possible to further optimize this because I don't really need to know the indices in idxs, but only how many there are.

I have been extensively looking at the source of NearestNeighbors.jl. My conclusion so far is that this would require me significantly tweaking the source to achieve this...

My only question is: is my assessment correct? Would only counting the inrange neighbors require indeed an extensive alteration of the source (which I would do in my code by writing several new versions of the source functions)? Or have I maybe missed a simple path?

(typical lengths of X are in the thousands to 10,000)

Jun 05 '20 19:06 Datseris

It would be good to:

Give the input data distribution. Is it just random points?
Rewrite the code to use the NearestNeighbors.jl API.

Jun 05 '20 19:06 KristofferC

Thanks for the quick reply, I appreciate it.

1

Unfortunately this cannot be known apriori, I am writing an algorithm to work with almost arbitrary input data as part of DynamicalSystems.jl. What I can say for sure are the following points:

Input data are not random data.
Input data may have total dimension $D$ but generally create a structure in data space with effective dimension smaller than $D$, sometimes much smaller than $D$. E.g. is a two dimensional dataset with effective dimension 1.2

2

Sure. Here is a full script that you could run if you want. It is not identical with the above, because I realized it is not necessary to exclude self-neighbors in this application (which is typically mandatory in other cases). I'm using DynamicalSystemsBase so you can access characteristic/representative data distributions.

using NearestNeighbors, Distances, DynamicalSystemsBase

function correlationsum(X, εs::AbstractVector, norm = Euclidean())
    d = distancematrix(X, norm)
    Cs = zeros(length(εs))
    N = length(X)
    @inbounds for (k, ε) in enumerate(εs)
        for i in 1:N
            @inbounds Cs[k] += count(d[j, i] < ε for j in i+1:N)
        end
    end
    return 2Cs ./ (N*(N-1))
end

function distancematrix(X, norm = Euclidean())
    N = length(X)
    d = zeros(eltype(X), N, N)
    @inbounds for i in 1:N
        for j in i+1:N
            d[j, i] = evaluate(norm, X[i], X[j])
        end
    end
    return d
end

function correlationsum_NN(X::Dataset, εs::AbstractVector, norm = Euclidean())
    tree = KDTree(X.data, norm)
    N = length(X)
    factor = 1/(N*(N-1))
    Cs = zeros(length(εs))
    @inbounds for (i, ε) in enumerate(εs)
        idxs = NearestNeighbors.inrange(tree, X.data, ε)
        for j in 1:N
            Cs[i] += length(idxs[j])
        end
    end
    Cs .*= factor
    return Cs
end

to = Systems.towel()
tr = trajectory(to, 5_000)

εs = ℯ .^ (range(-3, -1; length = 12))

@time Cs = correlationsum(tr, εs)
@time Cs_NN = correlationsum_NN(tr, εs)

on my PC I get

0.331378 seconds (5 allocations: 190.812 MiB, 32.11% gc time)
  0.800122 seconds (516.58 k allocations: 762.105 MiB, 26.12% gc time)

(Notice Cs_NN has slight numeric difference from Cs, I need to adjust the 1/N(N-1) factor)

Jun 05 '20 20:06 Datseris

Hi @KristofferC ,

I am now writing a paper about a competing algorithm I have for another quantity, that once computed can give similar outcomes with the correlation sum displayed here. My algorithm has performance scaling O(DNlog(N)), where N is the amount of data while D being the data dimension.

The correlationsum function I provided here has performance D N^2. However it is critical that I try to compare with the most performant version (at least in theory). The KDTree version here allocates all found neighbors in memory, which is not needed, and thus it is not the most performant in theory.

I've tried to find some papers that provide theoretical results, and this seems a good match: http://www.cs.utah.edu/~lifeifei/cis5930/kdtree.pdf as well as this presentation: https://sites.cs.ucsb.edu/~suri/cs130a/kdTree.pdf (final slide gives time complexities)

they report construction performance of N log(N), and single query performance sqrt(N + m) with m the "output size" (I have to do the query for all N points in the tree though). This result is for rectangular search, which I am not sure whether it coincides with the Euclidean distance in-range searching I use here. I am also not sure how the "output size" (number of neighbors to be reported I guess) can be known a-priori, since we do an in-range search...

Do you think you could tell me what would be the theoretical scaling of the in-range searches that we are interested in here from KDTrees.jl, assuming the found neighbors are not allocated? I would really appreciate that!

Jun 14 '20 10:06 Datseris

Optimized counting of inrange nearest neighbors

1

2