sumlog

[cscherrer]

This PR adds sumlog, a more efficient way to compute sum(log, x). There's more discussion on this on Discourse here: https://discourse.julialang.org/t/sum-of-logs/80370

EDIT: I think we have a good enough understanding of what's possible to lay out some design criteria. That ought to be more efficient than taking each line of code in isolation.

As a starting point, I suggest

1. Whenever sum(log ∘ f, x) is defined, sumlog(f, x) should give the same result (within some tolerance, etc)
2. sumlog(x) == sumlog(identity, x)
3. sumlog(f, x) should support a dims keyword argument whenever sum(log ∘ f, x) does (i.e., when x is an AbstractArray)
4. sumlog should be type-stable and compiler-friendly when possible
5. sumlog should use the optimized method requiring a single log application, whenever that's possible.

@devmotion @mcabbott thoughts on these?

[cscherrer]

@devmotion I guess we also need some ChainRules methods...

[devmotion]

@devmotion I guess we also need some ChainRules methods...

We could, but it's not necessary to do in this PR IMO.

Apart from the element type (see discussion above), I think the main problem left is that I assume the code is problematic for GPU arrays. Other array implementations in LohExpFunctions are written in a GPU-friendly way and should work with all array types.

[cscherrer]

I think the main problem left is that I assume the code is problematic for GPU arrays. Other array implementations in LohExpFunctions are written in a GPU-friendly way and should work with all array types.

Do you see a nice way of doing this?

I see two other potential things to add:

1. Support for Tuples and NamedTuples
2. Support for calling sumlog(f, x)

Both less critical, so we can come back to them

[cscherrer]

~~One of these updates along the way killed all of the performance. Are you seeing this too? Need to backtrack a bit I guess, and maybe split the preprocessing into a separate function~~

Got it

[cscherrer]

It got faster! Check it out:

julia> x = rand(1000);

julia> @btime sum(log, $x)
  6.362 μs (0 allocations: 0 bytes)
-1027.6

julia> @btime sumlog($x)
  986.857 ns (0 allocations: 0 bytes)
-1027.6

[cscherrer]

The function has to be added to the docs for the tests to pass.

I don't understand what you mean by this. Docstrings are usually added automatically, what's left to do?

[cscherrer]

I changed it to

function sumlog(x)
    T = float(eltype(x))
    _sumlog(T, values(x))
end

There's no need to restrict the type of x, and this allows it to be a Tuple or NamedTuple. For NamedTuples, calling values(x) makes it much faster, and this doesn't affect other types.

[devmotion]

What's left to do?

You have to add the function to docs/src/index.md.

[mcabbott]

For small arrays, calling log(prod(x)) is a few times quicker again.

On crude tests it doesn't seem less accurate when it works, although for large enough arrays it gives Inf. Can it be used as a fast path, maybe with a test for Inf afterwards to check if the "slow" path is required?

julia> for N in [10, 30, 100, 300, 1000]
         println()
         @show N
         xs = rand(N)
         @btime sum(log, $xs)
         @btime sumlog($xs)
         err = Float64(mean(abs(sum(log∘big, x) - sumlog(x)) for x in (rand(N) for _ in 1:100)))
         @show err
         @btime log(prod($xs))
         err2 = Float64(mean(abs(sum(log∘big, x) - log(prod(x))) for x in (rand(N) for _ in 1:100)))
         @show err2
       end

N = 10
  107.296 ns (0 allocations: 0 bytes)
  29.857 ns (0 allocations: 0 bytes)
err = 6.533083953902729e-16
  14.821 ns (0 allocations: 0 bytes)
err2 = 4.679379951051084e-16

N = 30
  241.358 ns (0 allocations: 0 bytes)
  70.983 ns (0 allocations: 0 bytes)
err = 2.2369534809836574e-15
  17.451 ns (0 allocations: 0 bytes)
err2 = 1.3853197780876373e-15

N = 100
  729.947 ns (0 allocations: 0 bytes)  # sum(log, x)
  218.037 ns (0 allocations: 0 bytes)  # sumlog(x), with a check for negative values (204.166 ns without)
err = 9.411386403503971e-15
  37.466 ns (0 allocations: 0 bytes)  # log(prod(x)), with no such check: 5x faster
err2 = 3.815901761052095e-15

N = 300
  2.213 μs (0 allocations: 0 bytes)
  623.547 ns (0 allocations: 0 bytes)
err = 2.239577037102115e-14
  108.782 ns (0 allocations: 0 bytes)
err2 = 1.4313227111152077e-14

N = 1000
  7.250 μs (0 allocations: 0 bytes)
  2.051 μs (0 allocations: 0 bytes)
err = 8.074581160990276e-14
  404.790 ns (0 allocations: 0 bytes)
err2 = Inf

[devmotion]

although for large enough arrays it gives Inf

I guess it should depend on the range of values in the array and could possibly happen even with very small arrays. That makes me wonder as well how much the errors in your example depends on the fact that you use only values in [0, 1).

[mcabbott]

Sure. My guess is that never doing this for long vectors is probably a sensible heuristic, guessing they will often overflow (and are expensive to traverse twice). For short ones, perhaps it needs some smarter check to see if it's safe. There is some time available, e.g. plenty to check sum(x), but small numbers will give problems too.

[tpapp]

I am skeptical about including this functionality. I agree that in some contexts (eg likelihood / posterior density calculations) users sum log densities, but usually they make a best effort to have those quantities already in logs. This is widely supported across the package ecosystem (cf Distributions.logpdf, etc). Taking a lot of logs explicitly in these calculations looks like a code smell.

@cscherrer, can you please explain where/why you need this? The discourse topic you link already takes that as a given.

[cscherrer]

It's pretty common for log-density to include a log(foo) term, where foo might be x, sigma, or something else. Regression problems require a sum of these, so this problem comes up any time the foo is not constant.

In GLM.jl, the gamma residual deviance is computed as

devresid(::Gamma, y, μ::Real) = -2 * (log(y / μ) - (y - μ) / μ)

So for example, if y and μ are vectors, a sum of these could be computed using

sumlog(y) - sumlog(μ)

or (maybe better?) by creating a MappedArray or LazyArray that looks like y ./ μ, and then calling sumlog on that.

[devmotion]

In GLM.jl, the gamma residual deviance is computed as

A bit unrelated, but using LogExpFunctions this could be implemented as

devresid(::Gamma, y::Real, μ::Real) = -2 * logmxp1(y / μ)

instead. This would be a bit faster:

julia> using LogExpFunctions, BenchmarkTools

julia> devresid_gamma(y::Real, μ::Real) = -2 * (log(y / μ) - (y - μ) / μ)
devresid_gamma (generic function with 1 method)

julia> devresid_gamma2(y::Real, μ::Real) = -2 * logmxp1(y / μ)
devresid_gamma2 (generic function with 1 method)

julia> @btime devresid_gamma(y, μ) setup=(y = rand(); μ = rand());
  8.527 ns (0 allocations: 0 bytes)

julia> @btime devresid_gamma2(y, μ) setup=(y = rand(); μ = rand());
  7.711 ns (0 allocations: 0 bytes)

[cscherrer]

@tpapp just making sure you saw my response to your concern

[tpapp]

@cscherrer: thanks for asking, and the original answer. I understand that this is sometimes done, but at the moment I am not convinced that the optimization is worth the extra code complexity. But if you have a user case, I am fine with including this.

Also, I don't know enough numerical analysis to understand the error behavior. More on that below.

[tpapp]

I played around with random tests and the new implementation is sometimes better (much better) and sometimes worse than sum(log, ...). It would be great to understand why and see if we can improve it further. Comparison of log10(abs(difference to BigFloat)):

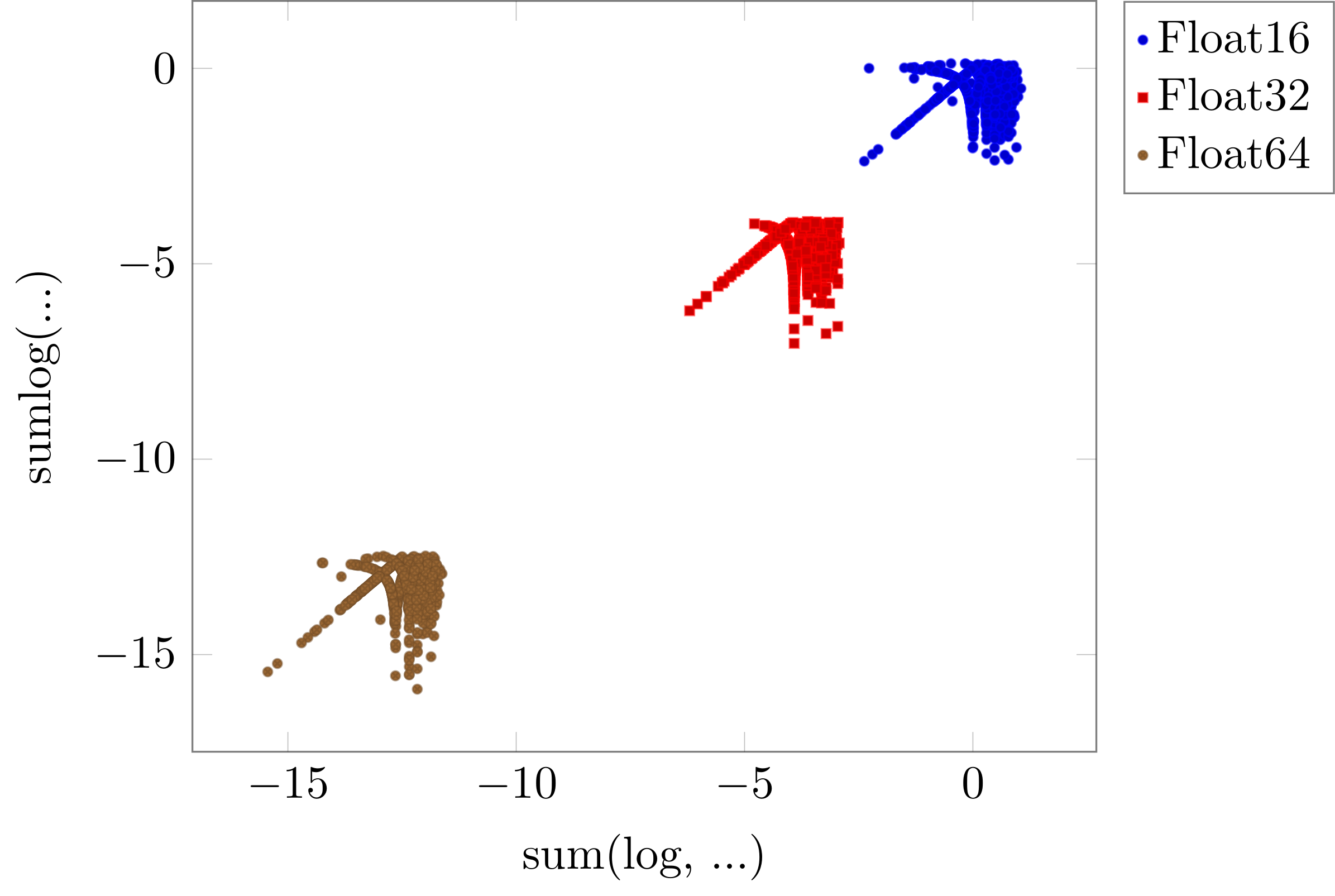
Code:

import Pkg; Pkg.activate(; temp = true)
Pkg.add(url = "https://github.com/cscherrer/LogExpFunctions.jl#master")
Pkg.add("PGFPlotsX")
using LogExpFunctions, PGFPlotsX, Random

function compare_randomly(rng, T, M = 2000)
    z = T.(randexp(M))
    precisely = sum(log, BigFloat.(z))
    precision(x) = T(log10(abs(x - precisely)))
    (precision(sum(log, z)), precision(sumlog(z)))
end

c16 = [compare_randomly(Random.GLOBAL_RNG, Float16) for _ in 1:1000]
c32 = [compare_randomly(Random.GLOBAL_RNG, Float32) for _ in 1:1000]
c64 = [compare_randomly(Random.GLOBAL_RNG, Float64) for _ in 1:1000]

@pgf Axis({ xlabel = "sum(log, ...)", ylabel = "sumlog(...)", only_marks,
            legend_pos = "outer north east", draw_opacity = 0.5, mark_size = 1},
          PlotInc(Coordinates(c16)),
          LegendEntry("Float16"),
          PlotInc(Coordinates(c32)),
          LegendEntry("Float32"),
          PlotInc(Coordinates(c64)),
          LegendEntry("Float64"))

[cscherrer]

The exponent computation is always exact, so I'd guess the worst case for this matches the worst case for prod

[mcabbott]

Maybe it's clearer to think in terms of how many nextfloats it's wrong by. Here's some code to try, results I see:

• The errors are very strongly correlated with those of sum(log, x).
• Changing it to accumulate sig::Float64 doesn't seem to help accuracy.
• When log(prod(Float64, x)) is finite, it appears to be equally accurate.

So far just tried with with scale * rand(N). With which, errors seem larger at N=10^3 than at 10^2 or 10^4, 10^5. Are there pathalogical choices of input which give much larger errors?

function countepsfrom(x::T, xtrue) where {T<:AbstractFloat}
    target = T(xtrue)
    for n in Iterators.flatten(zip(0:100, -1:-1:-100))
        nextfloat(x, n) === target && return n
    end
    nf = (target - x) / eps(x)
    return isfinite(nf) ? round(Int, nf) : nf
end
function countsumlog(xs::AbstractArray{T}, sig_bound...) where T
    ytrue = sum(log.(big.(xs)))
    ybase = sum(log, xs)
    yfast = sumlog(xs, sig_bound...)  # modified to allow sig = 1.0 of wider type, and to print when sig > bound
    yprod = T(log(prod(Float64, xs)))
    (base = countepsfrom(ybase, ytrue), fast = countepsfrom(ybase, yfast), prod = countepsfrom(ybase, yprod))
end
using Random

countsumlog([1,2,3.0])  # exact

[countsumlog(rand(1000)) for _ in 1:20]  # doesn't hit bound, worst error 14, very correlated

[countsumlog(rand(100)) for _ in 1:20]  # at this size, prod still works
[countsumlog(3200 * rand(100)) for _ in 1:20]  # at threshold, prod either Inf or good,

# Float32
countsumlog([1,2,3f0])  # exact

Random.seed!(1); [countsumlog(rand(Float32, 1000)) for _ in 1:20]  # all hit bound, larger errors, worst 17, perfectly correlated
Random.seed!(1); [countsumlog(rand(Float32, 1000), 1.0) for _ in 1:20] # accumulating in Float64 changes nothing

[countsumlog(rand(Float32, 100)) for _ in 1:20]  # here prod works, provided it accumulates Float64

# Float16
countsumlog(Float16[1,2,3])  # exact

Random.seed!(2); [countsumlog(rand(Float16, 1000)) for _ in 1:20]  # ditto, worst -18

[countsumlog(rand(Float16, 100)) for _ in 1:20]  # prod works fine
[countsumlog(3200 * rand(Float16, 100)) for _ in 1:20]  # same threshold for prod, since it uses Float64

[mcabbott]

The answer for pathalogical cases is numbers near to 1, one of which was in the tests. With my code just above:

julia> x1p = fill(nextfloat(1.0), 100);

julia> countsumlog(x1p)
(base = 0, fast = -77, prod = -77)

julia> x1m = fill(prevfloat(1.0), 100);

julia> countsumlog(x1m)
(base = 0, fast = -1970324836974592, prod = -39)

julia> (sum(log, x1m), sumlog(x1m))
(-1.1102230246251565e-14, -1.4210854715202004e-14)

ps. I think @tpapp's code needs Pkg.add(url = "https://github.com/cscherrer/LogExpFunctions.jl", rev="master") to run, and probably wants z = T.(randexp(rng, M)) else all the RNG stuff does nothing.

[tpapp]

@mcabbott: thanks for the correction, indeed I didn't use the RNG.

I think you are right. You can make a pathological example with eg

z = [1 + (eps(T) * ((i % 2) - 1)) for i in 1:1000]

for T = Float64 etc, where sum(log, ...) does dramatically better. My intuition for this is that all the precision is at the end of the mantissa, and multiplication does not preserve enough. I suspect that anything close to powers of 2 would do badly.

[cscherrer]

@devmotion @mcabbott @tpapp did you see the updated description in the OP? I think we could make some more progress by stepping back and reaching agreement on this. Then hopefully any questions on the code will be more stylistic. It's more like Test-Driven Development - we could even take an explicit TDD approach if you like.

BTW, I've thought of another example. The determinant of a matrix is the product of its eigenvalues, so the log-determinant is the sum of its log-eigenvalues. This example is interesting, because in this case we really want the "unsafe" version allowing negative eigenvalues. If our matrix happens to be triangular, we get a very fast way to compute logdet.

MeasureTheory includes parameterization according to the affine transform, so for example x = σ * z + μ where z is iid normal. In this case, σ is often triangular, so we get nice speedups.

[mcabbott]

The goals seem fine to me.

• Does goal 1 imply that 0.0 and NaN etc. should propagate as usual? They give errors with exponent, which I tried to work around, but it won't work for e.g. high-precision AbstractFloats in various packages. Not sure I timed a version with an if to shield this.
• I don't see how to do sum(log ∘ f, x; dims) without type-inference, since f could be (say) real-to-complex. Although possibly you could hide this my making it sumlog!(f, y, x), constructing y by the same path that mapreduce uses, and dispatching on y::AbstractArray{<:AbstractFloat}.

[devmotion]

I think it might be easier to focus on goals 1 (accuracy and consistency with sum(log, x)), 4 (type stability), 5 (performance), and GPU compatibility first. Supporting sumlog(f, x) and optional dims arguments seems less relevant initially.

Generally, I can see that the function can be useful in some cases but I would like to avoid that code complexity is increased too much in this package, so I think a simple implementation should be another main goal. IMO the code for logsumexp is already quite complex and hence difficult to maintain but probably this is justified by the popularity of this particular function.

[cscherrer]

• Does goal 1 imply that 0.0 and NaN etc. should propagate as usual?

Ideally, yes. But none of these are requirements in any way. The idea is more that if we start with an idealized wish list, it might be easier to talk about the design space and decide together where to make compromises.

Maybe this is just me, but after ten or so updates I find it too easy to get lost in the weeds. Maybe this can help keep us form going in circles in the discussion.

• I don't see how to do sum(log ∘ f, x; dims) without type-inference

I think to start we should focus on the real case. We can come back to complex numbers - maybe this could be a kwarg or optional type parameter, or even a separate function.

Supporting sumlog(f, x) and optional dims arguments seems less relevant initially.

If we use mapreduce, I think we get dims support almost for free, is that right?

Generally, I can see that the function can be useful in some cases but I would like to avoid that code complexity is increased too much in this package, so I think a simple implementation should be another main goal.

I like "as simple as possible, but no simpler". I can understand wanting to avoid Base._return_type, and to lean toward higher-order functions to help with AD. But one concern with simplicity is the potential for others to re-implement to avoid any shortcomings. IMO some degree of complexity is better than simple code no one uses.

---

Also... We could consider changing this function name to logprod. Note that sum(log, x) ≈ log(prod(x)), with sum(log, x) having a more restricted domain (no negative reals allowed), and log(prod, x) being faster, but much more likely to overflow or underflow.

So if it's easy to set it up so "double negatives cancel", logprod might be a better name.

[cscherrer]

This also points to another application - maybe you really want to just compute a product, but you'd like to avoid underflow and overflow. So for example @cjdoris's LogarithmicNumbers.jl would seem to benefit from adding

Base.prod(::Type{ULogarithmic}, x) = exp(ULogarithmic, logprod(x))

[devmotion]

avoid Base._return_type

Yes, this is part of the code complexity goal but will also improve stability of LogExpFunctions. All such internal functions and "hacks" should be removed from the PR, in particular since it seems they can be avoided easily. Even standard libraries such as Statistics don't use _return_type to handle empty iterators, see eg https://github.com/JuliaLang/Statistics.jl/blob/cdd95fea3ce7bf31c68e01412548688fbd505903/src/Statistics.jl#L204 and https://github.com/JuliaLang/Statistics.jl/blob/cdd95fea3ce7bf31c68e01412548688fbd505903/src/Statistics.jl#L170.

[tpapp]

@cscherrer: Regarding stepping back and agreement: I always think in terms of costs and benefits (code complexity and maintainability vs how useful the code is), and personally I would just go to logs as soon as possible, even at a slight performance cost. But if you really need this, I am fine with including it.

Regarding the goals:

1. I would rename to logprod, conveys the underlying algorithm and precision trade-offs better,

2. I think that dims and foo(f, x) are unnecessary, and it is silly that each function replicates the boilerplate for this, given that Julia has much nicer mechanisms now for these, but I understand that whenever we leave these out someone will complain

3. I would be happy with a robust and reasonably accurate logprod that is approximately sum(log, ...), with the understanding that someones one is better than the other. All algorithms have trade-offs and that's fine. Maybe we should document them though.

[cscherrer]

I've pushed another version. This time

1. It's logprod instead of sumlog
2. sumlog is still there for now, for easy comparison
3. I remembered about frexp. @mcabbott this behaves better for subnormals
4. I dropped dims, etc. I think we have a better understanding now of each other's priorities. I'm still in favor of more functionality, but we can start simple and get tests etc going. That will make it easier to weigh any drawbacks of adding more functionality.
5. I think this is a good candidate to go in Base. If we make it logabsprod it can be a big help to speed up logabsdet:

julia> x = LowerTriangular(randn(1000,1000));

julia> using LinearAlgebra

julia> using BenchmarkTools

julia> @btime logabsdet($x)
  8.687 μs (0 allocations: 0 bytes)
(-631.836, -1.0)

julia> d = diag(x);

julia> @btime logabsprod($d)
  1.202 μs (0 allocations: 0 bytes)
(-631.836, 1.0)

I cheated here a little, since we don't have (that I know of) a lazy diag in Base.

[mcabbott]

logprod is a neat idea to avoid checks.

frexp is also clearly what we were looking for. Does this have any effect on speed?

I am lost in all the noise on minor details, but checking sig > floatmax(typeof(sig)) / 2 is now the wrong thing, as it will overflow towards zero.

logprod should really have a case which tries log(prod()) first on small enough arrays, as this is much faster. (And it should advertise itself as being less prone to overflow than log(prod, rather than as being faster.)