How does xESMF treat missing values?

[jhamman]

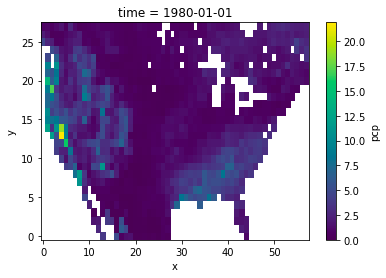
I have a use case where I am regridding from/to grids that have missing values in them (water mask over land). I'm curious how xESMF is treating these grid cells. I am noticing a large difference in how the grids come out between the bilinear and conservative regridding methods. For example:

bilinear:

conservative:

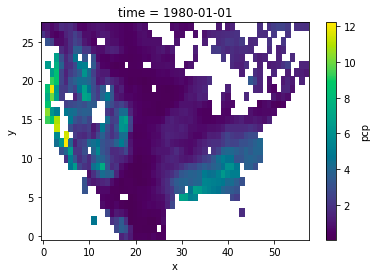
I should note, this regridding operation is a coarse-graining operation so there are up to 64 1/8th deg source grid cells going into each 1 deg dest grid cell.

[jhamman]

It seems that ESMF has options to specify src_mask_values and dst_mask_values but I don't see these in the xESMF source code at the moment.

The ESMF docs show a usage that looks something like:

regrid = ESMF.Regrid(srcfield, dstfield,
                     regrid_method=ESMF.RegridMethod.NEAREST_DTOS,
                     unmapped_action=ESMF.UnmappedAction.ERROR,
                     src_mask_values=mask_values)

refs: - http://www.earthsystemmodeling.org/esmf_releases/non_public/ESMF_7_0_0/esmpy_doc/html/api.html#masking

• http://www.earthsystemmodeling.org/esmf_releases/non_public/ESMF_7_0_0/esmpy_doc/html/examples.html

[bekozi]

In ESMPy, the mask is configured on the grid and "selected" in the regrid call. You'll need to merge any data variable masks with any spatial masks and set that on the grid (see this code for an example). You can then select the value used by ESMF to construct the mask in the regrid call. The *mask_values argument is used to allow changing masks based on the grid mask values...kind of specialized. As far as I know, you can use whatever integer values you want for the mask.

When masking, also pay attention to the zero_region argument as it affects the handling of missing values in the output field. That is if you are using ESMF's sparse matrix multiply. Set create_rh=False otherwise!

[jhamman]

Xarray uses np.nan as its missing value flag. I'm thinking ESMF is not handling this as expected in some cases (conservative regridding). Perhaps we just need to make some changes in xESMF to make ESMpy aware of the mask (or use a different fill value).

[JiaweiZhuang]

@jhamman The different behaviors you get from bilinear and conservative algorithms are actually expected. The handling of nan is explained in this comment. Let me cite myself:

xESMF has no idea about land/sea mask. It just maps nan in the input data to nan in the output data. Say a destination point receives contributions from 4 source points, as long as 1 out of the 4 source points is nan, the total contributions will add up to nan (because any_number + nan = nan). If you don't want the contributions from the other 3 points to be corrupted bynan, you may set the 4th point to 0 instead of nan

When coarse-graining, conservative regridding will average over a large number of small cells (8*8=64 in your case), while bilinear regridding will only average over the nearest 4 cells. That's why you see a lot of nan in the conservative case (especially in the middle-west ), but few nan in the bilinear case. I assume that there are some nans in the middle-west in the original data; they are "skipped" by bilinear algorithm but are caught by conservative algorithm.

I am not sure if an additional option for masking is needed. If I understand correctly, ESMPy's masking capability can be equivalently done by masking the input/output data itself, before or after the regridding computation.

[jhamman]

@JiaweiZhuang and @bekozi - thank you both for sticking with this issue. I am starting to understand the situation a bit better.

• In xarray, we can extract the "mask" from any DataArray using the notnull method.
• I understand that the current API does not do this. Moreover, the Regridder only looks at the coordinates when developing the weights (E.g. xe.Regridder(ds_in, ds_out, ...)) and not the data variables.
• One option that could be considered is a check during the weights generation step to see if either dataset has a mask variable. There may also be more intuitive way of determining the masks for the source/destination grids. The key point is that ESMpy allows for the specification of masks for both of these grids.

As a bottom line, I think it is incorrect to let xarray's mask nans propagate through regridding operations. Most of xarray's operators are nan skipping so it seems logical to me, that xESMF would take a similar approach.

I also want to be clear, I'm not asking anyone to do any work here. I'm mostly trying to understand the challenges in this area. If we can settle on a path forward, I wouldn't be surprised if I would contribute to this development.

[JiaweiZhuang]

Most of xarray's operators are nan skipping so it seems logical to me, that xESMF would take a similar approach.

It is true that xarray.DataArray.mean skips nan by default. But what does it mean by "skipping nans" in regridding operations? If one needs to treat nan as 0, simply convert nan to 0 before regridding.

Or do you mean some sort of "re-normalizing"? Say, if the weights for a destination point are [0.25, 0.25, nan, nan], you would like the weights to be converted to [0.5, 0.5, 0, 0]? I don't think ESMPy's masking functionality has such an advanced feature, but this should be easy to do by directly modifying the weight matrix, similar to this comment.

[jhamman]

Or do you mean some sort of "re-normalizing"? Say, if the weights for a destination point are [0.25, 0.25, nan, nan], you would like the weights to be converted to [0.5, 0.5, 0, 0]?

Something like that. I image that is how ESMpy uses the masks internally. Perhaps @bekozi can elaborate thought.

[bekozi]

There's quite a bit going on this discussion, so I apologize for glossing over anything...

@JiaweiZhuang is correct regarding the way masks are handled for the conservative case. Masks will drop cells if only one masked cell is mapped to a destination cell.

I don't have any experience working with nan values in ESMF opting for masks instead. If the decision is made to stick with nan over masks, we should chat with @oehmke more about the implications. Like mentioned above, the biggest concern is faulty normalization.

If configured properly, the mask on the source grid will lead to an appropriate normalization for weight factors with masked entries excluded in the final weight matrix. The destination mask will simply exclude entries in the weight matrix for its associated index. Dynamic masking (changing mask with time/level) was implemented recently in ESMF, but I think that is beyond the scope of this discussion.

Without fully understanding xarray internals, I would recommend the grid mask be constructed from the first time/level/whatever dimension of the data variable(s) unless provided by the user. Using boolean masks are a good idea as they can be quickly be converted to binary. I have seen masks on spatial coordinates too, so maybe it's best to incorporate that at the start. It may make sense to incorporate the idea of a "spatial mask" at a very high level in xarray that xESMF could reference for cases such as this. How to automatically construct the mask is tricky. Some climate simulations have the first timesteps masked entirely from cold starts. :cry:

If one needs to treat nan as 0, simply convert nan to 0 before regridding.

This will generally work, but may lead to different masked data and values when compared with a regrid + mask.

I don't think ESMPy's masking functionality has such an advanced feature, but this should be easy to do by directly modifying the weight matrix, similar to this comment.

Nothing like this that I'm aware of!

[jhamman]

If configured properly, the mask on the source grid will lead to an appropriate normalization for weight factors with masked entries excluded in the final weight matrix. The destination mask will simply exclude entries in the weight matrix for its associated index. Dynamic masking (changing mask with time/level) was implemented recently in ESMF, but I think that is beyond the scope of this discussion.

Thanks. This is what I was looking for. I'm going to experiment a bit with adding a mask variable to the grid datasets ds_in, ds_out and passing that to ESMpy.

I don't have any experience working with nan values in ESMF opting for masks instead. If the decision is made to stick with nan over masks, we should chat with @oehmke more about the implications. Like mentioned above, the biggest concern is faulty normalization.

This would also be good to sort out. xarray's nans are just sentinel values. I'm beginning to think there is no reason they should be included in any gridding operation.

[bekozi]

This would also be good to sort out. xarray's nans are just sentinel values.

I'm genuinely curious as well. @oehmke is on vacation for a bit. I'll check in with him on this when he gets back.

[JiaweiZhuang]

the mask on the source grid will lead to an appropriate normalization for weight factors

I did some tests with ESMPy masking, but could not get any "weight normalization" by using ESMPy mask. The effect of masking seems to be equivalent to setting input data to zero before regridding.

For full details please see this gist. I put some key results here.

Here're my test grids:

Several cells in the input data are set to nan:

Without any masking, nan in the input data will propagate to the output data:

With ESMPy masking, the output data get very low values (those near the mask):

Such an result is equivalent to setting nan to 0 before regridding. The resulting values should have been much higher (closer to surrounding cells) if there were any normalization. I believe @jhamman wants this sort of conversion: [0.25, 0.25, nan, nan] -> [0.5, 0.5, 0, 0] But ESMPy masking seems to be doing: [0.25, 0.25, nan, nan] -> [0.25, 0.25, 0, 0]

Did I understand correctly? If so, such a "masking" can be equivalent done by one line of pre-processing code (data[np.isnan(data)]=0.0) and doesn't need to be added to xESMF.

xarray's nans are just sentinel values. I'm beginning to think there is no reason they should be included in any gridding operation.

It is true that xarray.DataArray.mean skips nan by default. But implementing what you described needs some extra code outside of ESMPy. Also, what if all weights for a destination cell are all nan?

[JiaweiZhuang]

Just realized that ESMPy masking does make a difference for nearest neighbor algorithm. My above comment still hold for bilinear and conservative methods.

Full code available in this slightly modified gist.

nearest neighbor + setting nan to 0:

nearest neighbor + masking nan in ESMPy:

The masked cell are skipped during nearest-neighbor-search, so the values in second-nearest cells are used.

Also, the problem of "all weights are nan" does not exist in nearest-neighbor method. If a destination cell is over the ocean (say only land has valid values), a cell along the coast should be found as the nearest cell. I do see the usefulness of this case.

Is it possible to avoid the additional 'mask' variable in https://github.com/JiaweiZhuang/xESMF/pull/23? Say, just set some elements in the lat and lon variables in the grid object ds_in and ds_out to nan, to indicate masks? Am I missing anything🤔?

[bekozi]

@JiaweiZhuang Nice work on the thorough testing. In the interest of not leading us down the wrong path, I'll work through this with @oehmke when he gets back and present those results. We need to expand the masking docs as well to be more explicit!

[jhamman]

@JiaweiZhuang - thanks for doing some extra leg work. I agree we need to hear from the ESMF crew how best to proceed. In the end, I'll be happy if we can fully describe the ESMF behavior, even if #23 isn't merged.

[bekozi]

@JiaweiZhuang I've been investigating ESMF masking and have something to run by you. I am using a very simple case for bilinear regridding. There is a 4x4 source grid (squares) with a 3x3 destination grid (star circles) - you'll see these points with the single masked source element in the picture at the end of this post. The coordinates are regional spherical similar to your test grids.

The weight file generated with ESMF looks like:

netcdf weights {
dimensions:
	n_s = 20 ;
variables:
	double S(n_s) ;
	int col(n_s) ;
	int row(n_s) ;
data:

 S = 0.254167701295419, 0.254167701295418, 0.245832298704582, 
    0.245832298704581, 0.255115371771049, 0.255115371771049, 
    0.244884628228951, 0.244884628228951, 0.255447214127049, 
    0.255447214127049, 0.244552785872951, 0.244552785872951, 
    0.25544721412705, 0.255447214127049, 0.244552785872951, 0.24455278587295, 
    0.25544721412705, 0.255447214127049, 0.244552785872951, 0.24455278587295 ;

 col = 3, 4, 7, 8, 7, 8, 11, 12, 9, 10, 13, 14, 10, 11, 14, 15, 11, 12, 15, 16 ;

 row = 3, 3, 3, 3, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9 ;
}

You'll notice destination indices 1, 2, 4, 5 are missing in the row variable. So, ESMF drops the destination elements that are not fully mapped by four "corners" on the source. I was wrong about the normalization. Do you see similar behavior with xESMF and nan values? Dropping the partially mapped destination elements make sense from a POLA perspective...

[JiaweiZhuang]

@bekozi Thanks for the example. This agrees with my above results that masking a cell is mathematically equivalent to "setting the input data in that cell to zero" (in bilinear case).

One possible advantage of this masking approach (as opposed to zeroing-out the input data) is that it can save some computation by avoiding adding and multiplying on 0s. However, a disadvantage is that two separate regridders need to be built for unmasked and masked input data, even though the underlying grid is the unchanged.

The nearest-neighbor method is probably the only case where masking is useful (cannot be replicated by pre&post processing tricks). In your case, I expect that indices 1, 2, 4, 5 will be preserved in nearest-neighbor search. Note that this is only for "source to destination"; masking for "destination to source" should behave pretty much the same as for bilinear&conservative&patch, where some input cells are simply thrown away.

I was wrong about the normalization. Do you see similar behavior with xESMF and nan values?

The weight generation in xESMF exactly relies on ESMPy so the behavior is exactly the same.

[JiaweiZhuang]

We've been mostly talking about masking on source cells. On the other hand, masking destination cells seems pretty pointless because it is equivalent to zeroing-out destination cells after regridding.

However, destination masking should have some real effect on the "destination to source" nearest-neighbor method, where a masked destination cell should not be able to receive contribution -- according to the principle of 'nearest_d2s' that "a source point must be mapped to a destination point", a cell near the masked cell should receive the contribution instead. This cannot be replicated by simple pre&post-processing (just like source masking for 'nearest_s2d')

I frankly don't know the use case for 'nearest_d2s'. It might make sense for Grid<->LocStream conversion where you may want to aggregate/spread the data along the LocStream trajectory. For Grid<->Grid conversion, this algorithm is a bit weird...

[JiaweiZhuang]

Overall, I tend to accept @jhamman's proposal of adding a mask variable. I do see the (somewhat limited) usefulness of ESMPy masking, especially for nearest-neighbor methods. However, there needs to be a very clear documentation on the effect of masking, for different regridding algorithms.

[bekozi]

Hi, @JiaweiZhuang. If you don't implement masking, then nan values should be left in the field data to ensure the sparse matrix multiplication will create nan values appropriately in the destination field. This assumes your SMM operation containing a nan will return a nan. Setting nan to zero implies data is defined.

You will also need to be explicit that "masking" is handled on the field end during SMM by xESMF and degenerate grid coordinates are not supported. For the bilinear test case with the masked element, the weight file is portable as the source grid defines what is masked. Without the mask, the weight file would imply all field data built on that grid is defined at every location. That may be just fine (and preferable) depending on how the weight file is used, but it is something to consider when advising xESMF users on reusing weights.

Basically, it comes down to whether you want ESMF or xESMF to determine what is mapped/unmapped following a regridding operation and also if a grid or grid+field is required.

[bekozi]

degenerate grid coordinates are not supported

My bad - I need to be more specific. Degenerate coordinates support through nans will probably work by setting ignore_degenerate=True. This flag is best reserved for well understood cases and should not generally be used as it can hide errors you want to see like user code generating bad coordinates. Known coordinate issues could not be masked a priori. This is an edge case to be sure, but it is good to be aware of.

[jhamman]

Thanks both of you for keeping this conversation going. I've been busy working on other things but recently ran into how CDO treats this case. For conservative area remapping, there are two environment variable options that must get passed to the SCRIP library:

ENVIRONMENT
    CDO_REMAP_NORM
        This variable is used to choose the normalization of the conservative interpolation.
        By default CDO_REMAP_NORM is set to 'fracarea'. 'fracarea' uses the sum of the
        non-masked source cell intersected areas to normalize each target cell field value.
        This results in a reasonable flux value but the flux is not locally conserved.
        The option 'destarea' uses the total target cell area to normalize each target cell
        field value. Local flux conservation is ensured, but unreasonable flux values may result.
    REMAP_AREA_MIN
        This variable is used to set the minimum destination area fraction. The default
        of this variable is 0.0.

This seems to cover my personal use case (fracarea) and provide an option for more detailed handling.

[JiaweiZhuang]

This variable is used to choose the normalization of the conservative interpolation.

This is very similar to (probably the same as) #17.

But this normalization would not help if a destination cell has no overlap with unmasked source cells (i.e. all overlapping source cells are masked). You can still get some nan, say over the ocean or large lakes.

[JiaweiZhuang]

Degenerate coordinates support through nans will probably work by setting ignore_degenerate=True.

@bekozi thanks for the notice! How is "degenerate coordinates" exactly defined here? My understanding of a "degenerated grid cell" is when two corner points coincide and the cell becomes a triangle. But do you simply mean "masking" here?

[oehmke]

Hi @JiaweiZhuang, you are partially correct about what an ESMF considers a degenerate cell. Instead of two points collapsing to leave a triangle, for ESMF a degenerate cell is one where enough points collapse to leave a cell either a line or a point. Regarding the earlier question about fracarea, in ESMF we don't divide if the destination fraction is 0.0, so we don't get nans. (I think that was what you were asking (?))

[JiaweiZhuang]

@jhamman Just a quick note: the "re-normalization" you need can be enabled by applying masks and setting norm_type=ESMF.NormType.FRACAREA in ESMPy (#17). Only using masks without the new normalization option just means setting nan to 0.

One use case for this is to regrid emission data that is only defined over the land. With NormType.FRACAREA and masking, cells along the coast can get a realistic magnitude, instead of getting nan (default behavior) or getting low values (only masking, averaged with empty emission over the sea):

notebook example

This only works for conservative algorithm. There is no "re-normalization" for bilinear algorithm, where masking literally means zeroing nans.

[jhamman]

Thanks @JiaweiZhuang - this is exactly what I was going for.

[jhamman]

@JiaweiZhuang - circling back here. What do you think the next steps should be to resolve this issue. Your example above is compelling to the point I would like to see some explicit support for this use case in xESMF.

[JiaweiZhuang]

@jhamman It is in the masking branch right now:

pip install --upgrade git+https://github.com/JiaweiZhuang/xESMF.git@masking

regridder = xe.Regridder(grid_in, grid_out, method='conservative_normed')

where grid_in contains a 'mask' variable.

[NicWayand]

@JiaweiZhuang, just to clarify mask should be a coordinate as datasets are currently not handled?

[JiaweiZhuang]

@NicWayand mask is part of input/output grid (which are dataset), not input data fields. Masking is performed when building the regridder (modify the regridding weights), not when applying to data.