二叉树

[JTangming]

二叉树特点

• 每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点
• 左右子树是有顺序的，次序不能任意颠倒
• 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树
• 在二叉树的第 i 层上最多有 2^i-1 个节点（i >=1）

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，则为满二叉树

完全二叉树

对于具有 n 个节点的二叉树，对于任何一个编号 i (1 <= i <= n)，如果与同层级的满二叉树中编号为 i 的节点完全相同，则是完全二叉树。

注：满二叉树一定是完全二叉树，但反过来不一定成立。

二叉树的存储结构

顺序存储

二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。 如一颗完全二叉树如下： 顺序存储方式如下： 极端情况采用顺序存储的方式是十分浪费空间的，如：

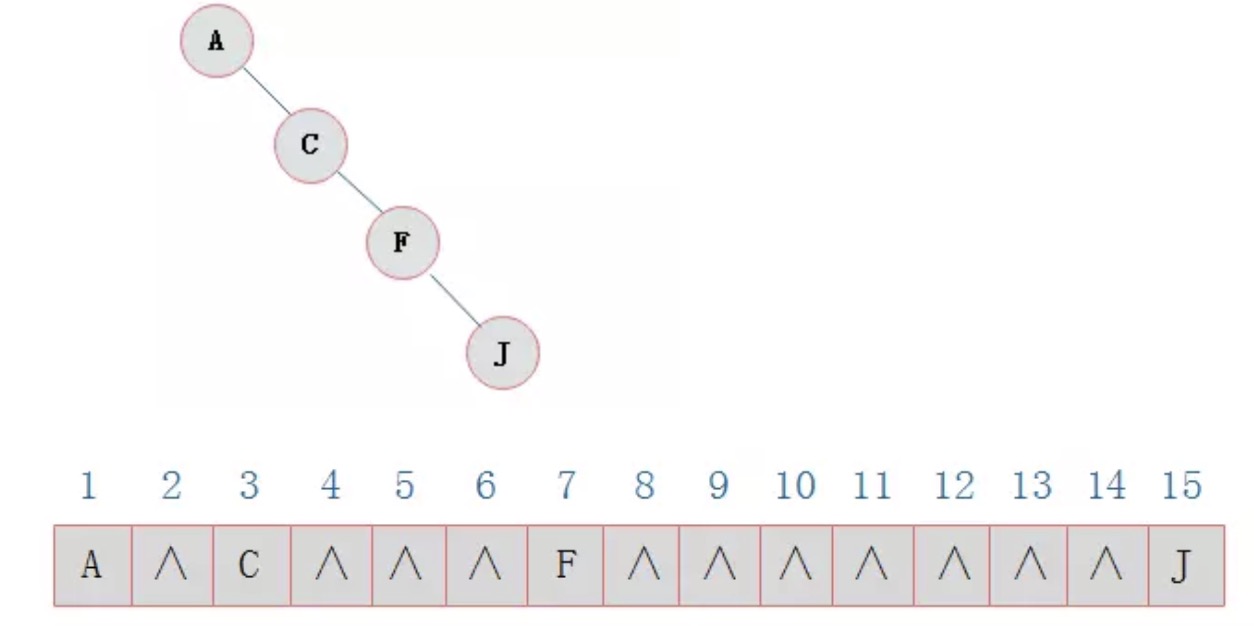
二叉链表

二叉链表将结点数据结构定义为一个数据和两个指针域，如：

二叉树遍历

• 前序遍历
• 中序遍历
• 后序遍历
• 层序遍历

快速记忆法： 前序就是父节点->左子树->右子树，中序是左子树->父节点->右子树，后序是左子树 -> 右子树 ->父节点

如这样一颗二叉树： 前序遍历输出为：ABDHIEJCFG 中序遍历输出为：HDIBJEAFCG 后序遍历输出为：HIDJEBFGCA 层次遍历结果为：ABCDEFGHIJ

[JTangming]

二叉查找树

又称二叉排序树，其特性：

• 左子树上所有结点的值均小于或等于它的根结点的值
• 右子树上所有结点的值均大于或等于它的根结点的值
• 左、右子树也分别为二叉排序树

如图：

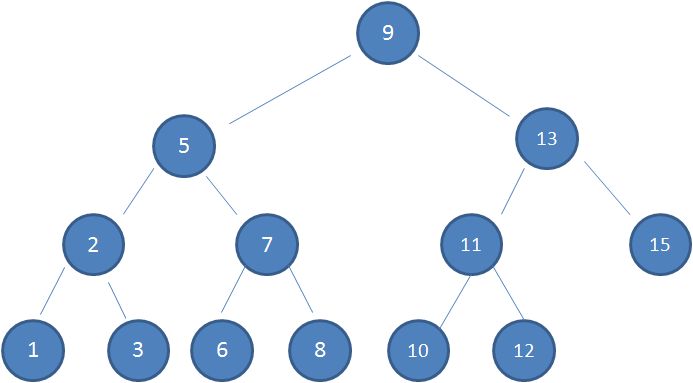
查找规则

• 如果二叉查找树为空，则返回空操作，否则，执行一下操作
• 先取根节点，如果节点 X 等于根节点，则返回
• 如果节点小于根节点，则递归查找左子树
• 如果节点大于根节点，则递归查找右子树

查找的最大次数等同于树的高度

插入

• 若树为空则直接将新节点插入，否则执行下面步骤
• 要插入的数据比根节点数据大，遍历右子树，如果右子树为空，则将新数据直接插入到右子节点的位置；不为空，则继续遍历右子树
• 要插入的数据比根节点数据小，遍历左子树，如果左子树为空，则直接将新数据插入到左子节点的位置；不为空，则继续遍历左子树

删除

删除可以从以下三种情形来理解，如图：

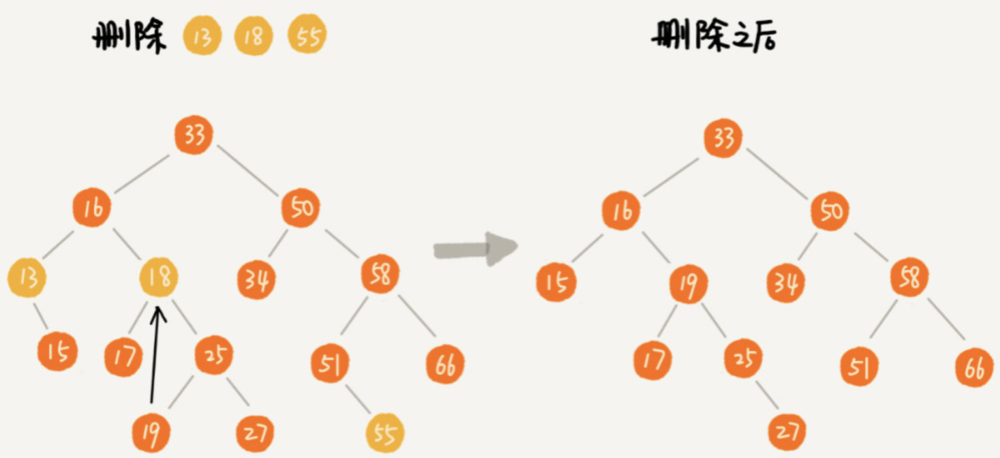
注：图来自于极客时间《数据结构与算法之美》专栏

• 要删除的节点没有子节点，修改父节点的指向为 null，如上图要删除的节点 55
• 要删除的节点只有一个节点，即只有左子节点或右子节点，则将要删除节点的父节点的指针指向要删除节点的子节点即可，如上图要删除的节点 13
• 果要删除的节点有两个子节点，则需要先找到这个节点右子树中的最小节点或者左子树中的最大节点，将其替换到要删除的节点上，然后删除这个右子树中的最小节点或左子树中的最大节点，如上图要删除的节点 18

缺点或者说是局限性

二叉搜索树最坏情况可能是链表，相应的时间复杂度是 O(n) 级别

红黑树

红黑树是一种自平衡的二叉查找树，除了符合二叉查找树的基本特征外，还具备：

• 节点是红色或黑色
• 根节点是黑色
• 每个叶子节点都是黑色的空节点（NIL节点）
• 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点