blog 曲线（路径）运动的那些事

曲线（路径）运动的那些事

Open JChehe opened this issue 5 years ago • 0 comments

曲线运动是指运动轨迹为曲线的运动。当物体运动的的速度与其所受到的合外力不在同一直线上时，物体便做曲线运动。典型的曲线运动有：平抛运动、斜抛运动、圆周运动等。——维基百科

引言

在 Web 页面中，直线运动很普遍，因为它实现简单的同时，也符合大多数场景。但是总有一些情况需要用到曲线运动。本文将曲线运动分为两种：「随机曲线运动」和「曲线路径运动」，后者是本文讲述的重点。而为了控制篇幅，部分章节以案例+外链的形式进行讲解。

直线运动

在阐述曲线运动前，我们先看看直线运动。

在二维的直角坐标系中，速度矢量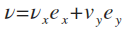速度公式。当合外力方向不变时（即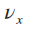、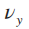等比缩放或不变），物体会保持初始方向进行直线运动。

See the Pen 直线运动 by Jc (@JChehe) on CodePen.

典型的曲线运动

当物体运动的的速度与其所受到的合外力不在同一直线上时，物体便做曲线运动。典型的曲线运动有：平抛运动、斜抛运动和圆周运动。

See the Pen 典型的曲线运动 by Jc (@JChehe) on CodePen.

动画动效

然而在网页动画中，元素并不一定符合物理世界的规律。因此，对设计稿中的曲线运动可选择以下实现方式：

三角函数
CSS 动画分层
逐帧法
贝塞尔曲线
动画库

实现方法肯定不止于此，更多的方法由大家去探索，欢迎大家留言分享。至于动画库，每个人的习惯或喜爱各不相同，本文就不再展开细说。

三角函数

三角函数看似简单，却在各类动画实现中承当了重要角色。比如：

cos 与 sin 的简单组合：

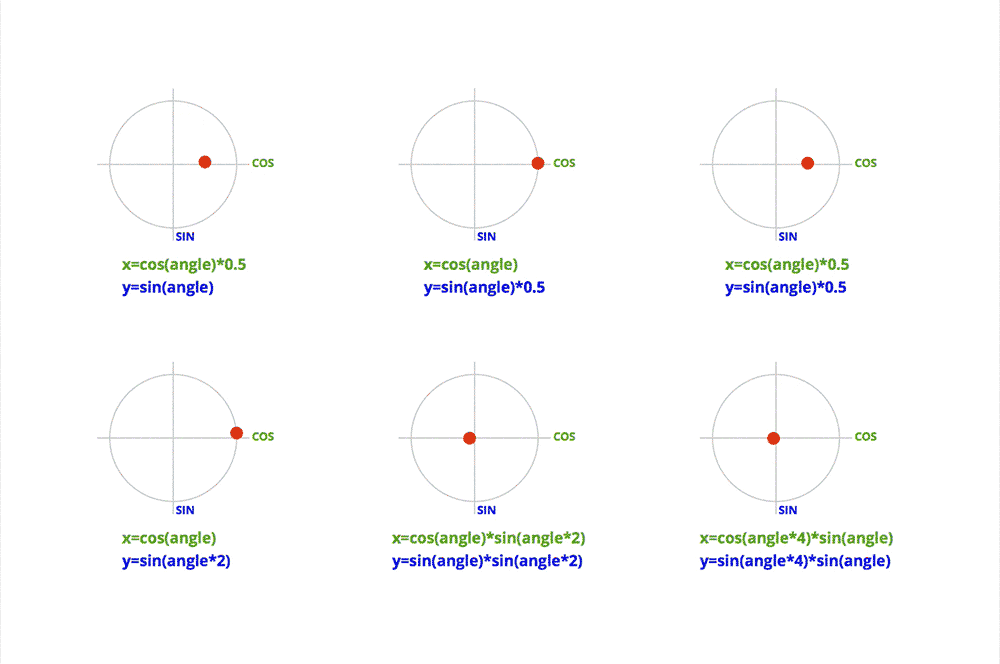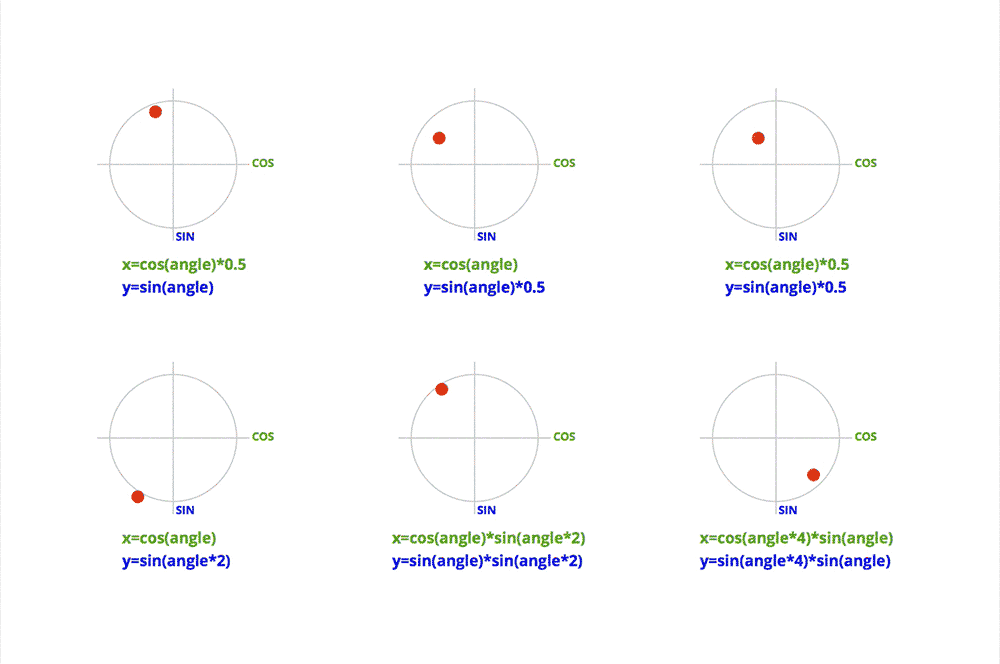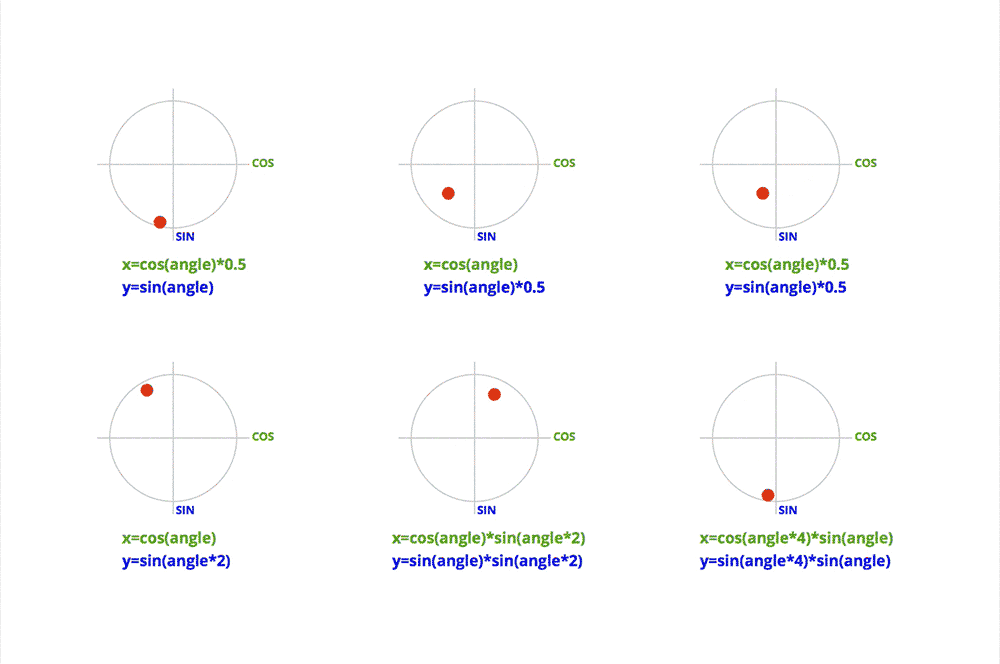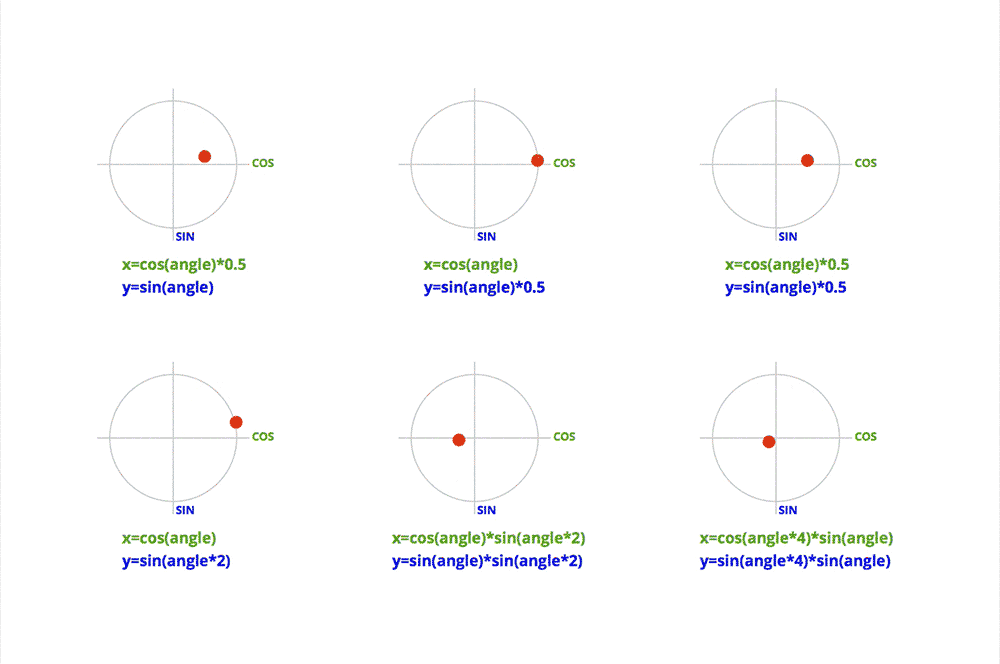
cos与sin的组合

Lissajous 曲线：

See the Pen Lissajous by Jake Albaugh (@jakealbaugh) on CodePen.

CSS 分层动画

在直线运动章节，我们知道：在二维的直角坐标系中，速度由 x 轴和 y 轴两个速度分量组成。因此通过 CSS 亦可实现曲线运动，具体可阅读《【译】使用 CSS 分层动画实现曲线运动》。

分享一下笔者之前基于该方式实现的背景氛围动效：

See the Pen css-curve-final by Jc (@JChehe) on CodePen.

逐帧法

然而，有些自定义的路径并不能简单地通过三角函数或 CSS 分层动画实现。假如设计师有提供 AE 稿，那么我们就可以考虑使用逐帧法去实现曲线路径运动。

See the Pen 逐帧曲线 by Jc (@JChehe) on CodePen.

上述案例存在两个曲线路径运动。因为曲线路径范围较小且无转向要求（物体是圆），采用逐帧的方式也能实现。

当然，逐帧并不是要求以 60 帧率去读取曲线信息，而是根据具体案例，以固定帧数间距取值作为关键帧，然后关键帧间使用线性过渡（animation-timing-function: linear;）即可。

因此，将光滑的曲线路径离散成固定帧数间距的点时，在视觉上也能提供曲线路径运动的效果。

「逐帧法」的确适用于小范围使用的案例，但显然不适用于复杂（或长距离）的曲线运动场景。

上述案例是从 AE 动画中提取曲线路径信息的，关于如何从 AE 中提取动画信息，可阅读《动画：从 AE 到 Web》。

贝塞尔曲线

在 Web 浏览器上，Canvas 和 SVG 都提供了绘制贝塞尔曲线的 API（二次与三次贝塞尔曲线）。但 SVG 比 Canvas 更贴心地提供了 animateMotion 路径动画。

SVG 路径动画：

See the Pen SVG Path motion by Jc (@JChehe) on CodePen.

要想在 Canvas 上实现与 SVG 一样的路径动画，本质是要实时获取路径在某时刻的 (x, y) 坐标。

以下图为例，路径由多段线段/曲线（以颜色区分）组成。

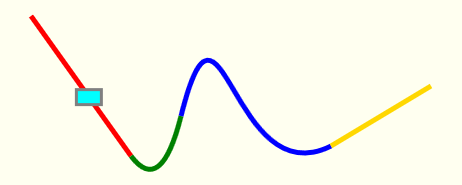曲线路径红色和金色为直线、绿色为二次贝塞尔曲线、蓝色为三次贝塞尔曲线

See the Pen 曲线路径运动 by Jc (@JChehe) on CodePen.

以下代码以百分比为参数（0.00 ~ 1.00）返回路径的 (x, y) 坐标。比如：

0.00 会返回路径初始位置的坐标。
0.50 会返回路径中间位置的坐标。
1.00 会返回路径结束位置的坐标。

线段特定位置的 (x, y)

以下代码是获取线段（直线）特定位置的 (x, y) 坐标：

function getLineXYatPercent(startPt, endPt, percent) {
  const dx = endPt.x - startPt.x
  const dy = endPt.y - startPt.y
  const X = startPt.x + dx * percent
  const Y = startPt.y + dy * percent
  return { x: X, y: Y }
}

二次贝塞尔曲线特定位置的 (x, y)

以下代码是获取二次贝塞尔曲线特定位置的 (x, y) 坐标：

function getQuadraticBezierXYatPercent(startPt, controlPt, endPt, percent) {
  const x = Math.pow(1 - percent, 2) * startPt.x + 2 * (1 - percent) * percent * controlPt.x + Math.pow(percent, 2) * endPt.x
  const y = Math.pow(1 - percent, 2) * startPt.y + 2 * (1 - percent) * percent * controlPt.y + Math.pow(percent, 2) * endPt.y
  return { x: x, y: y }
}

三次贝塞尔曲线特定位置的 (x, y)

以下代码是获取三次贝塞尔曲线特定位置的 (x, y) 坐标：

function getCubicBezierXYatPercent(startPt, controlPt1, controlPt2, endPt, percent){
  const x = CubicN(percent, startPt.x, controlPt1.x, controlPt2.x, endPt.x)
  const y = CubicN(percent, startPt.y, controlPt1.y, controlPt2.y, endPt.y)
  return { x: x, y: y }
}

// 三次贝塞尔曲线的辅助函数
function CubicN(pct, a, b, c, d) {
  const t2 = pct * pct
  const t3 = t2 * pct
  return a + (-a * 3 + pct * (3 * a - a * pct)) * pct
    + (3 * b + pct * (-6 * b + b * 3 * pct)) * pct
    + (c * 3 - c * 3 * pct) * t2
    + d * t3
}

将以上获取 (x, y) 坐标的方法结合在一起后，就可以实现图中的路径动画。

// 计算路径上特定位置的 (x, y) 坐标

if (pathPercent < 25) {
  const line1percent = pathPercent / 24
  xy = getLineXYatPercent({x: 100, y: 20}, {x: 200, y: 160}, line1percent)
}
else if (pathPercent < 50) {
  const quadPercent = (pathPercent - 25) / 24
  xy = getQuadraticBezierXYatPercent({x: 200, y: 160}, {x: 230, y: 200}, {x: 250, y: 120}, quadPercent)
}
else if (pathPercent < 75) {
  const cubicPercent = (pathPercent - 50) / 24
  xy = getCubicBezierXYatPercent({x: 250, y: 120}, {x: 290, y: -40}, {x: 300, y: 200}, {x: 400, y: 150}, cubicPercent)
}
else {
  const line2percent = (pathPercent - 75) / 25
  xy = getLineXYatPercent({x: 400, y: 150}, {x: 500, y: 90}, line2percent)
}

// 绘制物体（矩形）
drawRect(xy)

由于贝塞尔曲线的特性，百分比参数得到的点并没有拥有相同的弧长。如以下所示：

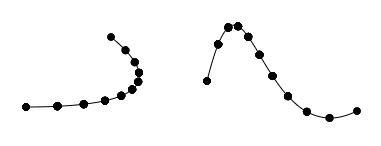贝塞尔曲线的点间距问题

左侧是二次贝塞尔曲线，右侧是三次贝塞尔曲线。通过 0, 0.1, 0.2,..., 1 间距打点后会发现曲线两端点比中间点的间距要大。想要达到两点间距相等的效果，可点击这里阅读了解。

物体的转向

See the Pen 曲线路径运动（带转向） by Jc (@JChehe) on CodePen.

SVG 的路径动画还支持物体实时跟随路径方向转向。为 animateMotion 标签指定 rotate="auto" 即可让物体指向即时速度方向（即点 P 的切线方向）。

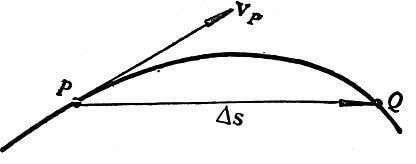
在曲线运动中，物体在某点的速度方向就是该点的切线方向（指向前进一侧）

既然我们能得到路径任意位置的坐标，那么我们就可以通过「当前位置」与「相邻位置」的坐标计算出该点的斜率，然后再根据斜率对物体进行旋转。

斜率，亦称“角系数”，表示一条直线相对于横轴的倾斜程度。一条直线与某平面直角坐标系横轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率。如果直线与x轴垂直，直角的正切值无穷大，故此直线不存在斜率。——百度百科

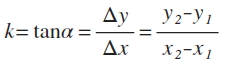
求线段斜率

// 获取两点之间的角度（弧度）
function getAngleOfTwoPoints (point1, point2) {
  return Math.atan2(point2.y - point1.y, point2.x - point1.x) // [-Math.PI, Math.PI]
}

See the Pen 两点角度 by Jc (@JChehe) on CodePen.

得到切线与 x 轴的夹角后，即可通过 context.translate() 与 context.rotate() 对物体旋转至切线方向。关于如何在 Canvas 中以物体为中心进行旋转的问题，建议读者阅读《canvas 图像旋转与翻转姿势解锁》，以深入了解 Canvas 的坐标系及相关知识。

Math.atan2() 与 Math.atan() 的区别

细心的同学可能发现 JavaScript 还有 Math.atan() 这个 API。Math.atan2() 与 Math.atan() 都是正切 tan(θ) 的反函数。

在 MDN 文档中可知两者有以下区别：

Math.atan2() 接受单独的 y 和 x 参数（注意参数顺序），而 Math.atan() 接受两个参数的比值（dy/dx）；
Math.atan() 仅返回半圆区间的值 (-Math.PI / 2, Math.PI / 2]（正 x 轴为 0），而 Math.atan2() 则返回整个圆的值 (-Math.PI ~ Math.PI]；
Math.atan2() 能正确处理 x = 0 而 y = 0 的情况，而 Math.atan() 不能。

Math.atan(0 / 0); // NaN, (0 / 0) 本来就是 NaN
Math.atan2(0, 0); // 0

// Math.atan2(y, x) 表示 (0, 0) 到 (x, y) 的直线与正 x 轴形成的夹角
Math.atan2(-1, 1); // -Math.PI / 4，即 -45°
Math.atan2(1, 1); // Math.PI / 4，即 45°

因此在一般情况下更推荐使用 Math.atan2(y, x)。

Math.atan2() 返回的角度为何是这样？

Math.atan2() 返回的角度如下图左侧所示，这似乎与平时课本上的不一样。

角度对比

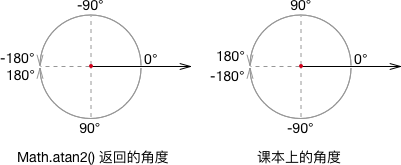
在 MDN 上对 Math.atan2() 有这样的描述——"This is the counterclockwise angle, measured in radians, between the positive X axis, and the point (x, y)."。重点是“This is the counterclockwise angle”，翻译过来是“这是一个逆时针角度”。

其实，课本中的角度正是“逆时针角度”。既然两者均是“逆时针角度”，为何表现得不一致呢？

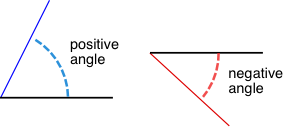
逆时针角度：逆时针为正，顺时针为负

其实，两者是一致的。之所以表现不一致，是因为 Canvas 坐标系的 y 轴往下为正（x 轴往右为正）。

Canvas 坐标系的历史背景是：电子枪是从左往右，从上往下扫描屏幕的。——《HTML5 + JavaScript 动画基础》

因此，只需将坐标系沿 x 轴翻转 180° 即可使 Math.atan2 还原成课本中的样子。

坐标系装换

当然，在 Canvas 中涉及角度的方法无需还原成课本上的样子，因为它们所处环境是一致的，比如：Math.atan2() 得到的角度可让 context.rotate() 方法直接使用。所以，我们并不需要将坐标系进行翻转，只需理解为什么在 Canvas 中正角度表现为“顺时针”即可。

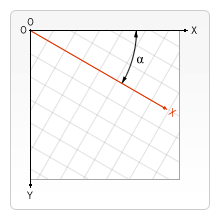
context.rotate(angle)

另外，笔者在搜索“逆时针角度”的资料时，顺便填充了生活常识的一个空白：一般情况下，时钟指针是顺时针走的，水龙头是顺时针关闭的，螺丝是顺时针拧紧的，罗盘方位是顺时针走的，但角度是逆时针测量的。

获取线段/贝塞尔曲线的长度

贝塞尔曲线案例中，四段子路径的运动时间相同。倘若想让物体在整个路径中速度保持不变，那么就需要得到每段子路径的路径长度，以分配与路径长度成比例的帧数（时间）。

下面是计算线段、二次贝塞尔曲线和三次贝塞尔曲线长度的计算方法：

线段的长度

设两个点 A、B 以及坐标分别为 A(x1, y1)、B(x2, y2) 两点距离

以下代码是获取线段长度：

function getLineLength (startPt, endPt) {
 return Math.sqrt(Math.pow(startPt.x - endPt.x, 2) + Math.pow(startPt.y - endPt.y, 2))
}

二次贝塞尔曲线的长度

以下代码是获取二次贝塞尔曲线长度：

// 来自：https://gist.github.com/tunght13488/6744e77c242cc7a94859
function getQuadraticBezierLength(p0, p1, p2) {
  var ax = p0.x - 2 * p1.x + p2.x
  var ay = p0.y - 2 * p1.y + p2.y
  var bx = 2 * p1.x - 2 * p0.x
  var by = 2 * p1.y - 2 * p0.y
  var A = 4 * (ax * ax + ay * ay)
  var B = 4 * (ax * bx + ay * by)
  var C = bx * bx + by * by

  var Sabc = 2 * sqrt(A+B+C)
  var A_2 = sqrt(A)
  var A_32 = 2 * A * A_2
  var C_2 = 2 * sqrt(C)
  var BA = B / A_2

  return (A_32 * Sabc + A_2 * B * (Sabc - C_2) + (4 * C * A - B * B) * log((2 * A_2 + BA + Sabc) / (BA + C_2))) / (4 * A_32)
}

See the Pen 二次贝塞尔曲线的路径长度 by Jc (@JChehe) on CodePen.

三次贝塞尔曲线的长度

目前没有一个简单的公式能直接获取三次贝塞尔曲线的长度，所以建议将曲线分为 N 段，然后将每段作为线段（直线）进行累加长度。所谓的分段，就是通过百分比参数获取路径上的值，然后再计算相邻两点的距离。当然，N 越大结果就越精准。

See the Pen 三次贝塞尔曲线的路径长度 by Jc (@JChehe) on CodePen.

以下代码是获取三次贝塞尔曲线长度：

function getCubicBezierLength(startPt, controlPt1, controlPt2, endPt, steps) {
  const points = []
  let sum = 0

  for (let i = 0; i < steps + 1; i++) {
    const percent = i * (1 / steps)
    const xy = getCubicBezierXYatPercent(startPt, controlPt1, controlPt2, endPt, percent)
    points.push(xy)
  }

  for (let i = 0; i < points.length - 1; i++) {
    const curPt = points[i]
    const nextPt = points[i + 1]
    sum += getLineLength(curPt, nextPt)
  }
  return sum
}

// 根据 percent 获取三次贝塞尔曲线的 (x, y) 坐标
function getCubicBezierXYatPercent(startPt, controlPt1, controlPt2, endPt, percent) {
  var x = CubicN(percent, startPt.x, controlPt1.x, controlPt2.x, endPt.x);
  var y = CubicN(percent, startPt.y, controlPt1.y, controlPt2.y, endPt.y);
  return ({
    x: x,
    y: y
  });
}

// 三次贝塞尔曲线的辅助函数
function CubicN(pct, a, b, c, d) {
  var t2 = pct * pct;
  var t3 = t2 * pct;
  return a + (-a * 3 + pct * (3 * a - a * pct)) * pct + (3 * b + pct * (-6 * b + b * 3 * pct)) * pct + (c * 3 - c * 3 * pct) * t2 + d * t3;
}

function getLineLength(startPt, endPt) {
  return Math.sqrt(Math.pow(startPt.x - endPt.x, 2) + Math.pow(startPt.y - endPt.y, 2))
}

总结

其实本文是笔者一直想写的主题，毕竟很多有趣的动画或多或少都会拥有曲线（路径）运动。当然，很多成熟的动画库都已经可以轻松实现曲线（路径）运动，但这也不妨碍笔者去学习总结相关知识。尽管，很多公式都是搜索来的。

参考资料

Oct 31 '18 16:10 JChehe

blog blog copied to clipboard

曲线（路径）运动的那些事

引言

直线运动

典型的曲线运动

动画动效

三角函数

CSS 分层动画

逐帧法

贝塞尔曲线

线段特定位置的 (x, y)

二次贝塞尔曲线特定位置的 (x, y)

三次贝塞尔曲线特定位置的 (x, y)

物体的转向

Math.atan2() 与 Math.atan() 的区别

获取线段/贝塞尔曲线的长度

线段的长度

二次贝塞尔曲线的长度

三次贝塞尔曲线的长度

总结

参考资料

blog
blog copied to clipboard