About the y_likelihoods
Sorry to bother you, I am recently been in the area of compression, take VARIATIONAL IMAGE COMPRESSION WITH A SCALE HYPERPRIOR as example, what is the meaning of each element in y_likelihoods matrix("likelihoods": {"y": y_likelihoods})?
Please see the following two sections:
- https://yodaembedding.github.io/post/learned-image-compression/#probabilistic-modeling-for-data-compression
- https://yodaembedding.github.io/post/learned-image-compression/#entropy-modeling
Briefly, each element of y is encoded using a probability distribution p. The y_likelihoods represent the value p(y).
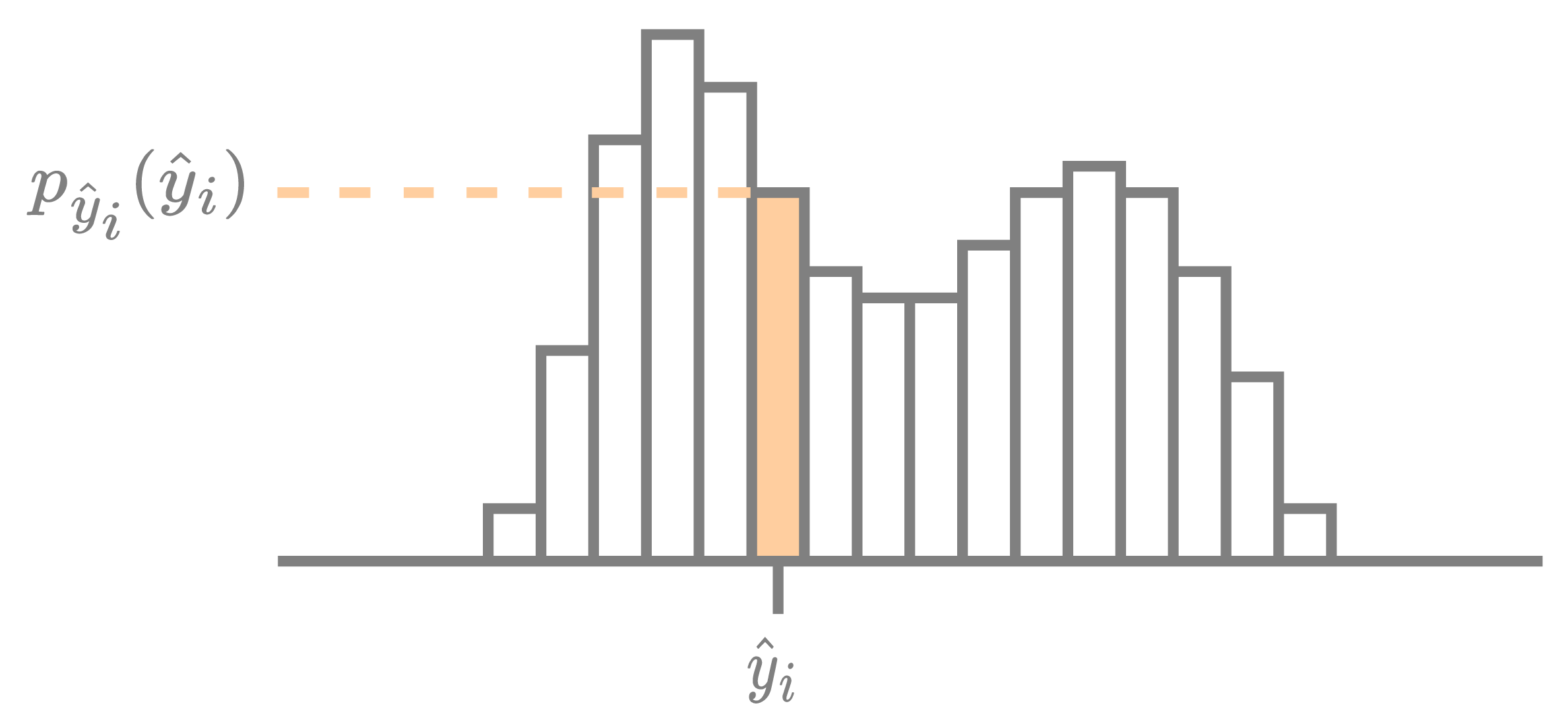
A given element $\hat{y}_i \in \mathbb{Z}$ of the latent tensor $\boldsymbol{\hat{y}}$ is compressed using its encoding distribution $p_{{\hat{y}}_i} : \mathbb{Z} \to [0, 1]$, as visualized in the figure below. The rate cost for encoding $\hat{y}_i$ is the negative log-likelihood, $R_{{\hat{y}}_i} = -\log_2 p_{{\hat{y}}_i}({\hat{y}}_i)$, measured in bits. Afterward, the exact same encoding distribution is used by the decoder to reconstruct the encoded symbol.
Visualization of an encoding distribution used for compressing a single element $\hat{y}_i$. The height of the bin $p_{\hat{y}_i}(\hat{y}_i)$ is highlighted since the rate is equal to the negative log of this bin.
Thank you for your reply! I really appreciate it!!I still have some issues to ask: (1) I remove the compression of z and directly predict scales from latent y. Then I pass the scales into GaussianConditional(None) for compression.(Because I want to use compression task as an auxiliary task.) Does it make sense? (2) I output the max value of y_likelihoods,the max value reaches 1.Is it normal? I feel so confused! Hoping for your reply!
- The exact same scales need to be available at the decoder, so you will need to transmit them to the decoder as well.
Everything should work fine as long as the decoder can reconstruct the exact same distribution used for encoding.ENCODER ==== Communication channel ====> DECODER - A likelihood of $p_{{\hat{y}}_i}({\hat{y}}_i)= 1$ means the rate cost is $R_{{\hat{y}}_i} = -\log_2 p_{{\hat{y}}_i}({\hat{y}}_i) = 0$ bits. That's the best-case scenario — being able to predict exactly what the decoded value is, without any uncertainty.
Thank you so much! I have another question:how can I calculate the y_likelihoods if I don't use quantization(add uniform noise)(Because I want to apply it to my research domain)
Sorry to bother you again.The element of y_likelihoods represents the value p(yi).Is p(yi) the probability that the symbol yi appears? If so,how is it ensured that the sum of the probabilities of all symbols appearing is equal to 1?
For the $i$-th symbol, there is a probability distribution $f_i : \mathbb{Z} \to [0, 1]$. (I called it $p_{{\hat{y}}_i}$ earlier.) By definition, $\int_{-\infty}^{\infty} f_i(t) \, dt = 1$.
But how is $f_i$ determined? For the mean-scale hyperprior,
- To encode $\hat{y}_i$, we use the $\mu_i$ and $\sigma_i$ that is outputted by $h_s$, and construct a Gaussian from it: $f_i(t) = \mathcal{N}(t ; \mu_i, \sigma_i^2)$.
- To encode $\hat{z}_i$, we use whichever $f_i$ that is learned by the “fully factorized” entropy bottleneck's small fully-connected network for the respective channel.