Set a reasonable default decay rate for EMANorm

[yawen-d]

Summary

We see there are two parameters controlling the typology of weight distribution (i.e., the shape of the graph): decay rate and num_timesteps.

1. Smaller decay rate leads to putting less weight on the transitions that are not very far away:
2. The weight on the first sample can be considerably high during the early stage of training.

My best guess is to set the decay rate between 0.999-0.9997.

Background

imitation.util.networks.EMANorm sets its default decay rate as 0.99, which could be too low. https://github.com/HumanCompatibleAI/imitation/blob/0cdae2b8072fca62470d09d1df67e2b780174008/src/imitation/util/networks.py#L138

Thanks to @taufeeque9 for the initial discussion in the previous thread and for providing the code for plotting. Below is how our implementation of EMA and EMV works: the past transitions are weighted as follows (for N+1 examples): $\alpha, \alpha \cdot \gamma, \alpha \cdot \gamma^2, ..., \alpha \cdot \gamma ^ {N-1}, \gamma ^ N$ with $\alpha = 1- \gamma$. All these weights sum to $1$ for all $N>0$. So the code for plotting the weights is:

import numpy as np
import matplotlib.pyplot as plt
num_timesteps = int(1e3) * 10
decay = 0.99

def plot_weights(decay, num_timesteps, normalize=True):
    x = np.linspace(0, num_timesteps, num_timesteps+1)
    y = (decay**x)
    y[:-1] *= 1-decay
    assert abs(y.sum()-1) < 1e-6, "weights (y) should sum to 1."
    if normalize:
        y = y / y.max()  # Normalize array y for readability
    plt.plot(x, y, label=f'{decay}')
    
plot_weights(decay, num_timesteps, normalize=True)
plt.legend()

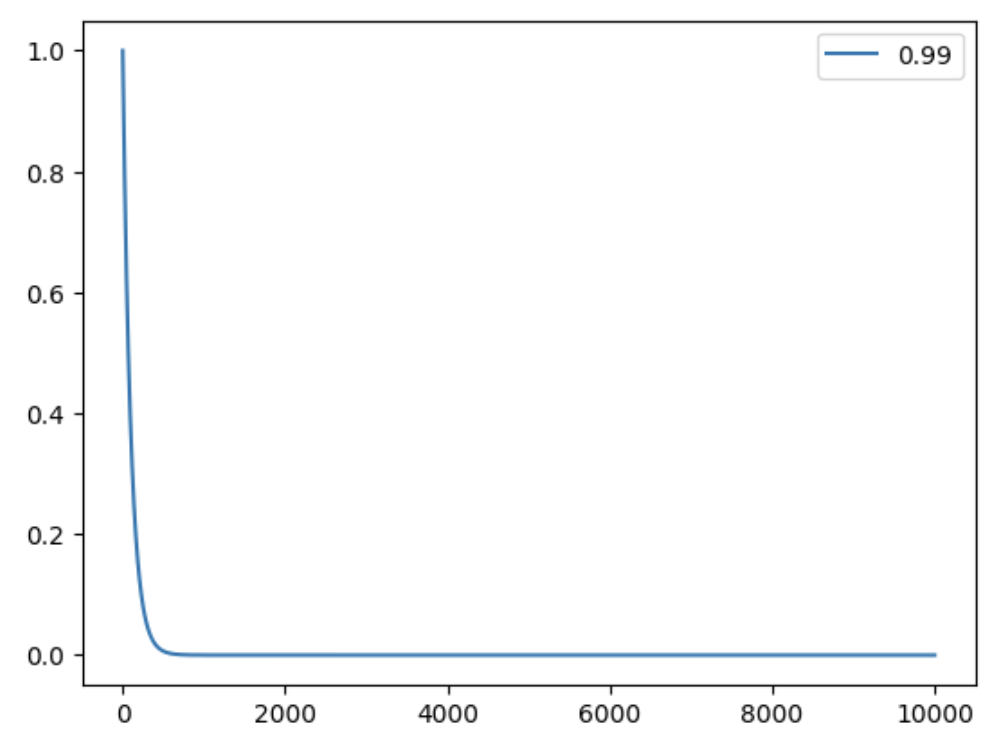
Problem Description

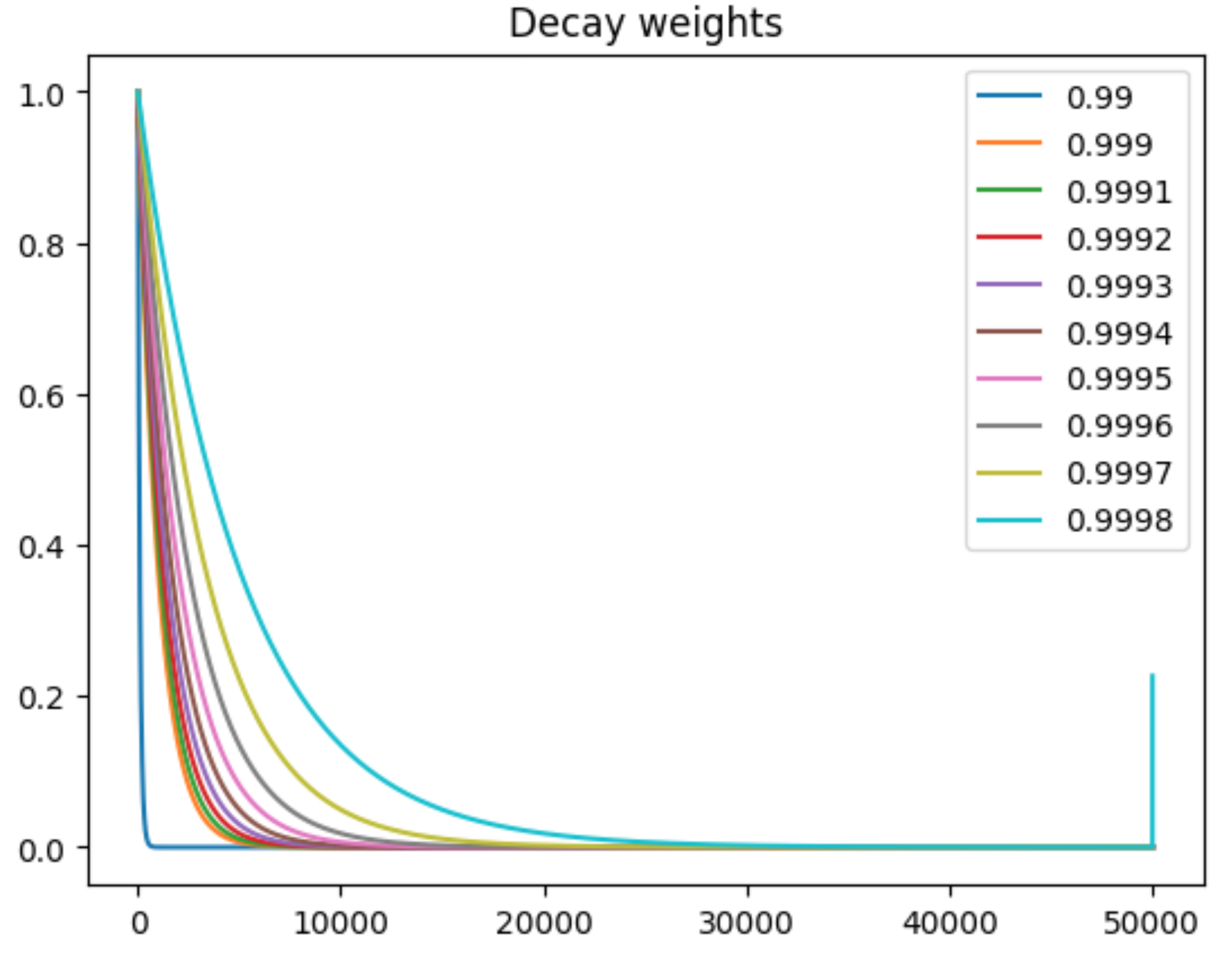
We see there are two parameters controlling the typology of weight distribution (i.e. the shape of the graph): decay rate and num_timesteps.

1. Smaller decay rate leads to putting less weight on the transitions that are not very far away:

import numpy as np
import matplotlib.pyplot as plt

num_timesteps = int(1e3) * 30
decay_list = [0.9, 0.99, 0.995, 0.999, 0.9995, 0.9997]

for decay in decay_list:
    plot_weights(decay, num_timesteps, normalize=True)
plt.legend(decay_list)

With the above code, we can plot the following:

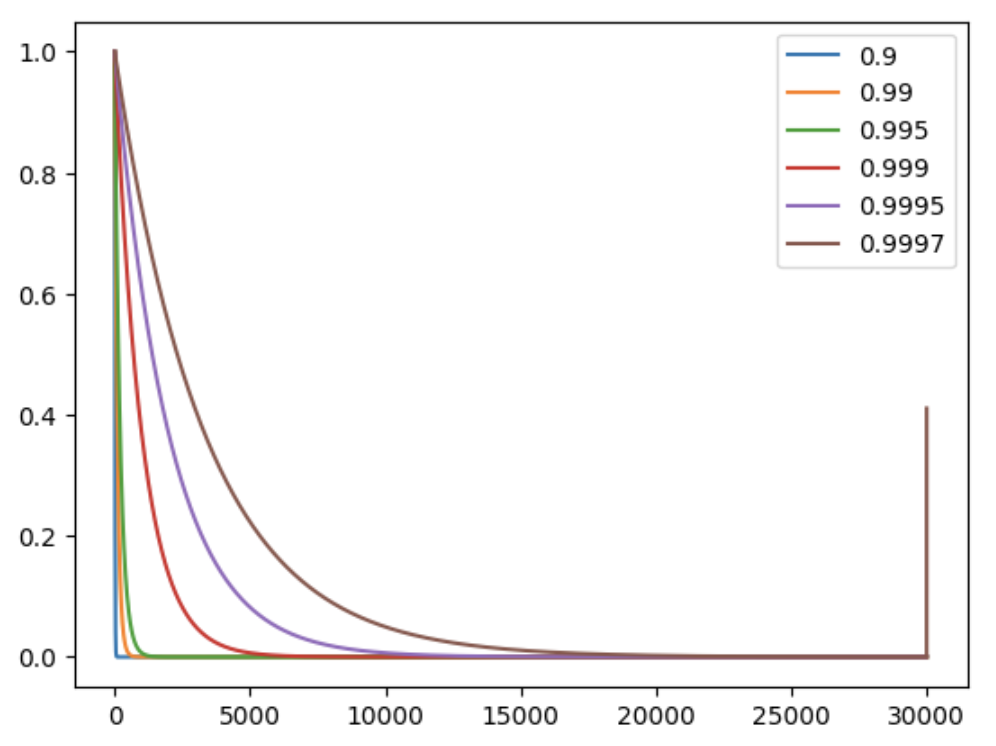
From the plot (I normalize the y-axis to [0,1] for readability) above, we noticed that decay rates below 0.999 only attend to fewer than 5 trajectories. You might also notice for 0.9997, there is a sharp upward turn at 30000 timesteps. This is because the weights include a term $\gamma^N$, which can be enormous if $N$ is small. This will be discussed in the bullet point below.

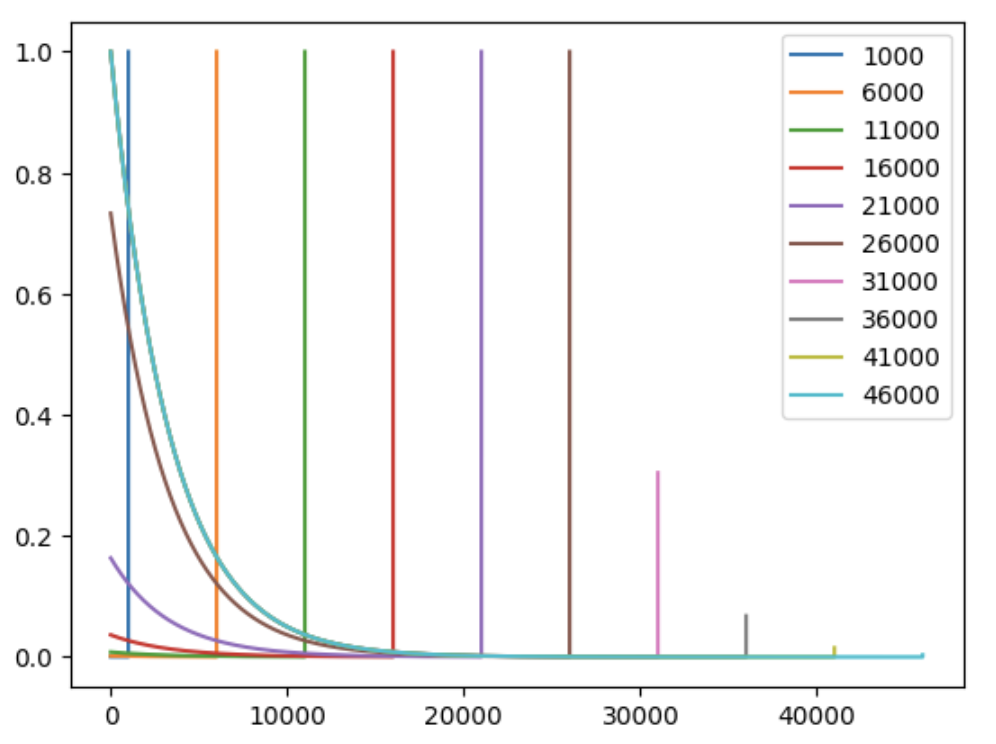
2. The weight on the first sample can be considerably high during the early stage of training.

As discussed above, the sharp upward turn exists for large $\gamma$ and small $N$. Specifically, the sharp turn will soon after $\gamma ^ N < \alpha$ . We can plot the weights with various $N$ below:

import numpy as np
import matplotlib.pyplot as plt

num_timesteps_list = [int(1e3) * n for n in range(1, 21, 2)]
decay = <some_decay>

for num_timesteps in num_timesteps_list:
    plot_weights(decay, num_timesteps, normalize=True)
plt.legend(num_timesteps_list)

gamma	0.99	0.999	0.9997
plot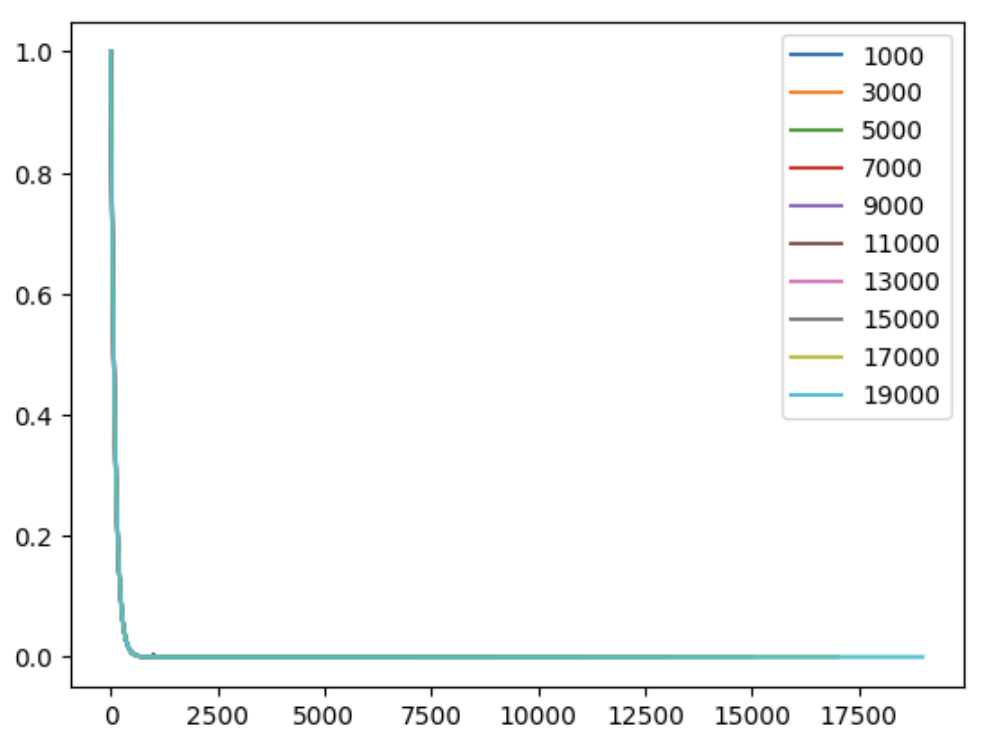

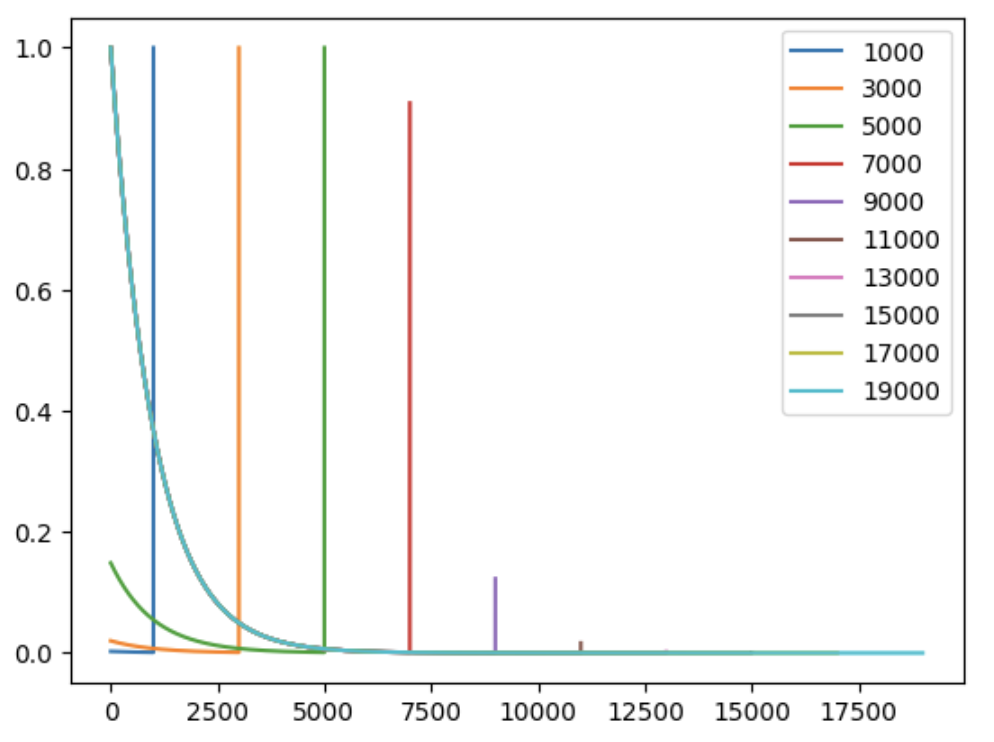For example, if we set $\gamma=0.999$, the sharp turn appears before $N=10000$ and disappears afterward.

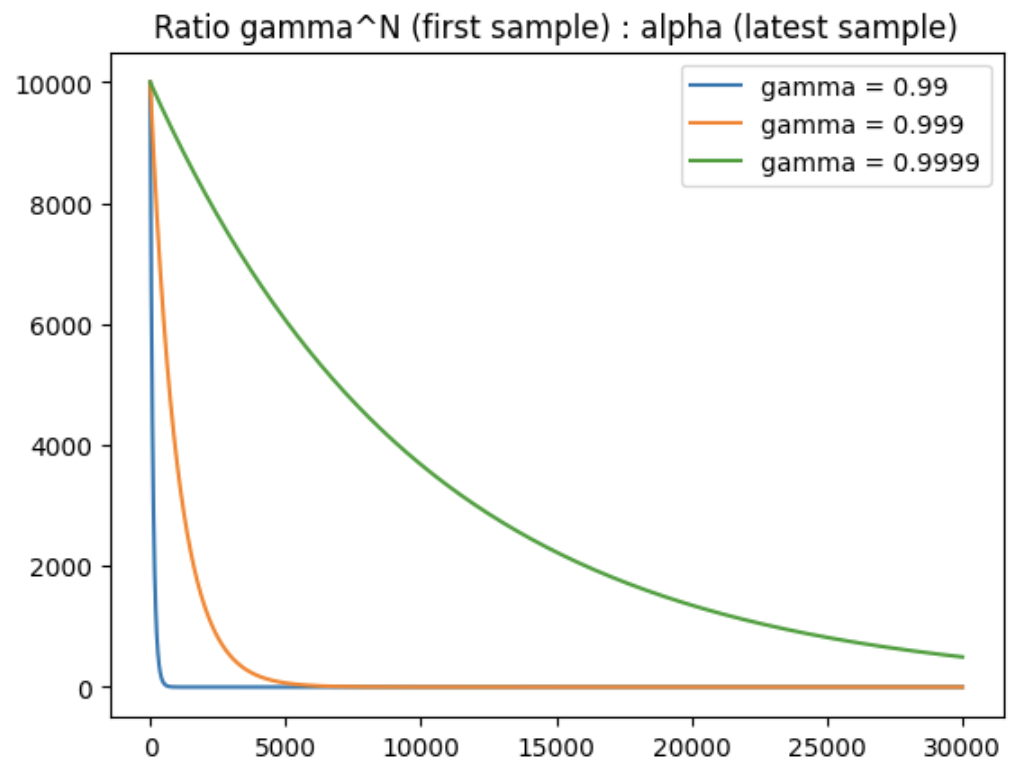
To be more specific, the ratio of weights between the latest sample and the first sample is $\gamma^N / \alpha$ will decrease as $N$ goes larger:

num_timesteps = int(1e3) * 30
decay_list = [0.99, 0.999, 0.9999]
alpha = 1 - decay
for decay in decay_list:
    x = np.linspace(0, num_timesteps, num_timesteps+1)
    y = decay**x / alpha
    plt.plot(x, y, label=f"gamma = {decay}")
plt.title("Ratio of gamma^N (first sample) : alpha (latest sample)")
plt.legend()

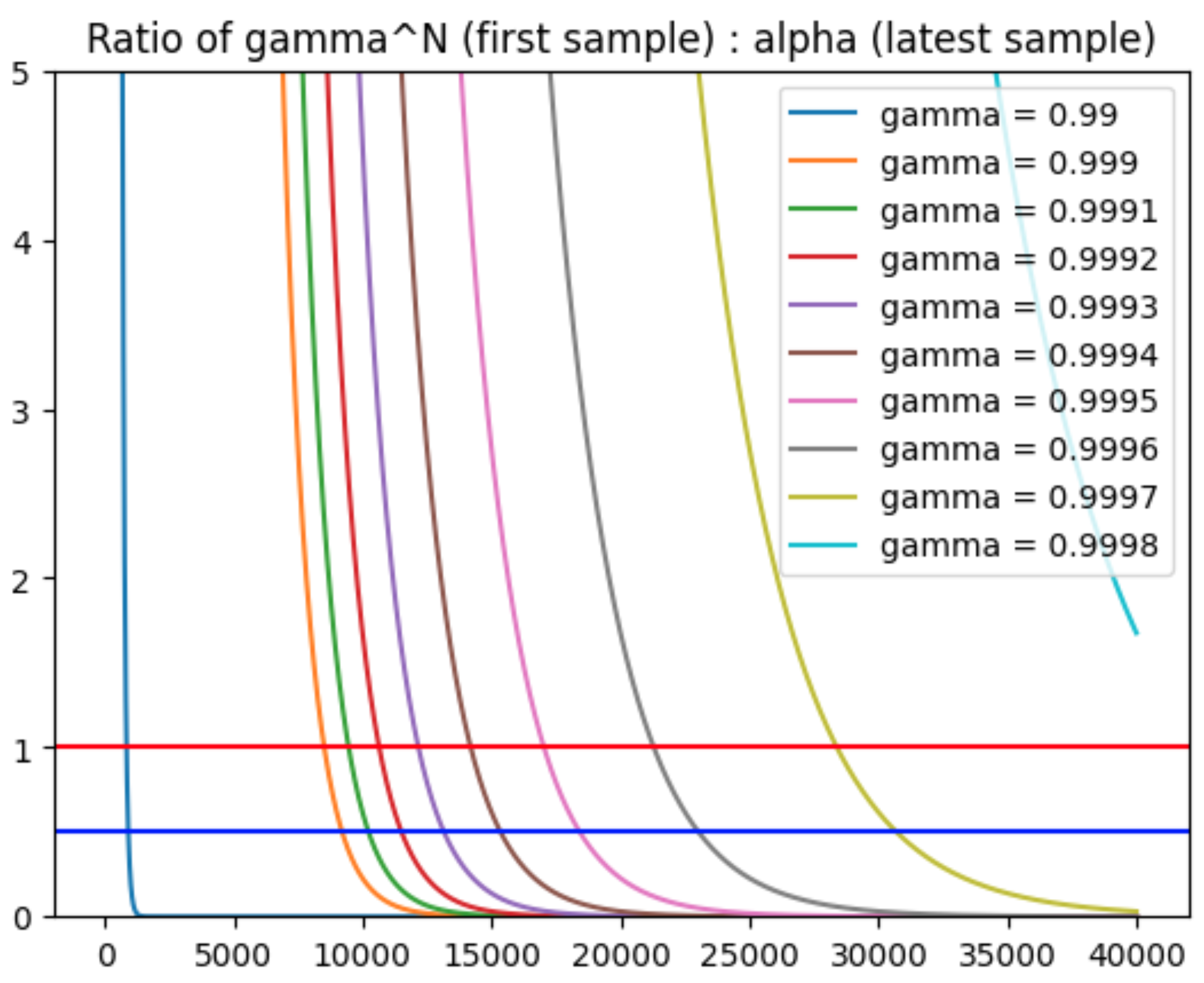
My best guess

• The decay rate could be set between 0.999-0.9997 to balance the above two problems:
  • To keep the ratio of first_sample:latest_sample below 1 after 10000-30000 timesteps
  • To keep more than the weights of more than one trajectories > 0.1.

Conclusion

• Although the weight on the first sample can be considerably high during the early stage of training, this problem can be neglected as the typical environments (e.g., DM Control) we use have a horizon length of 1000, so I think as long as this problem would disappear after 10-20 trajectories, it might be OK?
• What's more important might be to set a decay rate higher than 0.99 because we want the EMANorm to set significant weights beyond one single trajectory.
• My best guess is to set the decay rate between 0.999-0.9997.

[AdamGleave]

@yawen-d is this still an unresolved issue or are the defaults sensible now that we have https://github.com/HumanCompatibleAI/imitation/pull/546 ?

[AdamGleave]

Bump -- did https://github.com/HumanCompatibleAI/imitation/pull/546 resolve this? I'll close this soon if I don't hear back.

[yawen-d]

Yep, I think #546 resolved this. I will close this issue now.