Optimize EMANorm by removing for loop over a batch

[taufeeque9]

Description

Kept the incremental version of EMANorm in update_stats_incremental. Implemented the exact algorithm for computing EMA without any for loops. The runtime of the function has decreased by a factor of ~10. Now, the order of runtime is the same as that of RunningNorm.

Also, updated the code to compute EMA at the very first step too. Earlier, simple mean and average were computed in the first step.

Testing

Added a new test to compare the batch computation of EMA with the original incremental version of EMA. Also removed one test case (test_running_norm_identity_train) for EMA since it is not applicable for EMA. Earlier the test was passing since we were computing simple mean and variance at the first step.

[codecov[bot]]

Codecov Report

Merging #522 (5bd23d8) into master (cad41eb) will increase coverage by 0.01%. The diff coverage is 100.00%.

@@            Coverage Diff             @@
##           master     #522      +/-   ##
==========================================
+ Coverage   96.94%   96.95%   +0.01%     
==========================================
  Files          84       84              
  Lines        7420     7457      +37     
==========================================
+ Hits         7193     7230      +37     
  Misses        227      227              

Impacted Files	Coverage Δ
src/imitation/util/networks.py	98.05% <100.00%> (+0.03%)	:arrow_up:
tests/util/test_networks.py	100.00% <100.00%> (ø)

:mega: We’re building smart automated test selection to slash your CI/CD build times. Learn more

[AdamGleave]

Thanks for the PR! Changes look reasonable to me at a high level, my suggestions are fairly minor apart and largely to do with improving clarity.

I'm tagging @levmckinney to take a look at this as he wrote the original version. In particular I think we were a bit dissatisfied with details of the old implementation (e.g. the random permutation part is a bit hacky), but went that route largely due to simplicity. It's possible after this refactor there's an alternative that's cleaner. If not then happy to stick with the current semantics (I expect in practice these implementation differences won't really matter anyway).

[AdamGleave]

Thanks for putting the PDF together Lev!

I don't follow the 2nd step in lemma 2, where the denominator switches from 1-alpha to 1-w_{m,m}. I thought w_{m,m} was alpha/b -- so wouldn't these only agree in the case b=1?

On Mon, 8 Aug 2022, 06:01 Lev McKinney, @.***> wrote:

@.**** commented on this pull request.

In src/imitation/util/networks.py https://github.com/HumanCompatibleAI/imitation/pull/522#discussion_r939804538 :

• def update_stats(self, batch: th.Tensor) -> None:

•    """Update `self.running_mean` and `self.running_var` in batch mode.
  

•    Args:
  

•        batch: A batch of data to use to update the running mean and variance.
  

•    """
  

•    b_size = batch.shape[0]
  

•    batch = batch.reshape(b_size, -1)
  

•    # Shuffle the batch since we don't don't want to bias the mean
  

•    # towards data that appears latter in the batch
  

•    perm = th.randperm(b_size)
  

•    batch = batch[perm]
  

•    # geometric progession of decay: decay^(N-1),...,decay,1
  

•    weights = th.vander(th.tensor([self.decay]), N=b_size).T
  

•    alpha = 1 - self.decay
  

•    if self.count == 0:
  

Coming back to this again I think I've finally figured out the correct incremental algorithm. I've attached in bellow with a proof of correctness,

Incremental EMA with batches.pdf https://github.com/HumanCompatibleAI/imitation/files/9278587/Incremental.EMA.with.batches.pdf

— Reply to this email directly, view it on GitHub https://github.com/HumanCompatibleAI/imitation/pull/522#discussion_r939804538, or unsubscribe https://github.com/notifications/unsubscribe-auth/AALZ3I4H4OGGVTGM7L3JO4LVYCBAJANCNFSM55ZGYWNA . You are receiving this because your review was requested.Message ID: @.***>

[taufeeque9]

@AdamGleave Yes, alpha = b * w_{m,m}. So the denominator should in step 2 should be (1 - b * w_{m, m}). This factor of b would go away in step 5 because the weights sum to 1/b (in the proof this mistake cancels out with the mistake you mentioned).

Thanks for putting the PDF together Lev! I don't follow the 2nd step in lemma 2, where the denominator switches from 1-alpha to 1-w_{m,m}. I thought w_{m,m} was alpha/b -- so wouldn't these only agree in the case b=1? … On Mon, 8 Aug 2022, 06:01 Lev McKinney, @.> wrote: @.* commented on this pull request. ------------------------------ In src/imitation/util/networks.py <#522 (comment)> : > + def update_stats(self, batch: th.Tensor) -> None: + """Update self.running_mean and self.running_var in batch mode. + + Args: + batch: A batch of data to use to update the running mean and variance. + """ + b_size = batch.shape[0] + batch = batch.reshape(b_size, -1) + # Shuffle the batch since we don't don't want to bias the mean + # towards data that appears latter in the batch + perm = th.randperm(b_size) + batch = batch[perm] + # geometric progession of decay: decay^(N-1),...,decay,1 + weights = th.vander(th.tensor([self.decay]), N=b_size).T + alpha = 1 - self.decay + if self.count == 0: Coming back to this again I think I've finally figured out the correct incremental algorithm. I've attached in bellow with a proof of correctness, Incremental EMA with batches.pdf https://github.com/HumanCompatibleAI/imitation/files/9278587/Incremental.EMA.with.batches.pdf — Reply to this email directly, view it on GitHub <#522 (comment)>, or unsubscribe https://github.com/notifications/unsubscribe-auth/AALZ3I4H4OGGVTGM7L3JO4LVYCBAJANCNFSM55ZGYWNA . You are receiving this because your review was requested.Message ID: @.***>

[levmckinney]

I've attached the PDF giving the proofs for the update rule: Incremental_batch_EMA_and_EMV.pdf The latex source code can be found here

[yawen-d]

I'm a bit not sure what a good way should be to test the correctness or convergence of the EMA running stats. I'm mainly unsure about

1. How to set the default decay rate?

We don't have a way to customize the decay rate of EMANorm yet. See below: https://github.com/HumanCompatibleAI/imitation/blob/a6c79e9378a9a2d571bcf11c40846c6db86f3b3f/src/imitation/rewards/reward_nets.py#L434

Most likely I think we can directly set a reasonable value and not change it afterwards. The current default decay rate is set to be 0.99, which may be too low. https://github.com/HumanCompatibleAI/imitation/blob/a6c79e9378a9a2d571bcf11c40846c6db86f3b3f/src/imitation/util/networks.py#L138

Consider an environment of horizon length == 1000 (which is the case for all environments in DM Control), 0.99^1000=0.00004317, so the EMA already ignores early transitions within a single trajectory. I currently set a default decay=0.9997 based on the intuition to put weights on the past 10 trajectories because 0.9997^(1000*10)=0.04976466. This isn't precisely how EMA works, but it gives a general idea of how much weights we set on the past trajectories.

Below is the plot for

decay_list = [0.9, 0.99, 0.999, 0.9997, 0.9999]
num_timesteps = 10000

x = np.linspace(0, num_timesteps, 10000)
for decay in decay_list:
    y = decay**x
    plt.plot(x, y)

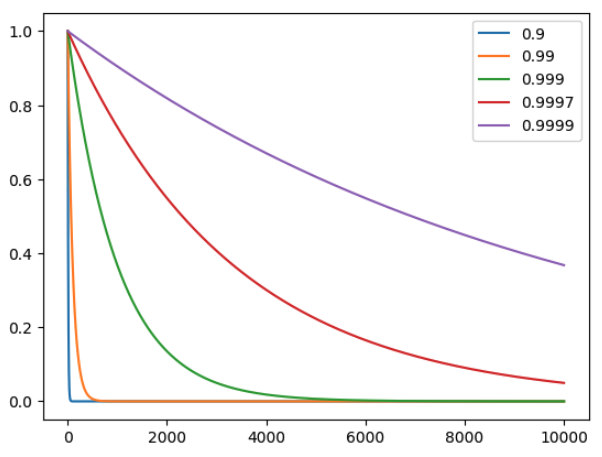
2. How to set reasonable values of rtol and atol in th.testing.assert_close()? For example, if I change the default decay rate to 0.9997 (see #538), some of the current tests (e.g. test_parameters_converge) won't pass, although this could be alleviated by increasing num_samples.

In summary, there are two decision-relevant takeaways:

1. How do we set the default decay rate of EMANorm?
   • My current guess is to set 0.9997 based on my intuition, but still lack a more principled way of setting this.
2. How do we design the tests in tests/util/test_networks.py when the results could be sensitive to the decay rate? (e.g. test_running_norm_eval_fixed; test_parameters_converge; test_ema_norm_batch_correctness)
   • My current guess is to set reasonable stats, such as
     • Set num_samples to be >1000 instead of 100
     • Perhaps no need to test unreasonable decay rates (e.g. 0.5)
     • Not sure how to set rtol and atol

[taufeeque9]

Thanks for the analysis Yawen! I also had my doubts regarding setting the default decay rate to 0.99. However, I think it is a reasonable decay rate, and any rate above 0.99 might not be suitable.

In the code @yawen-d referenced, there's a slight problem. The weights should also be multiplied by $\alpha$ (which is 1 - $\gamma$) for all the elements except the first one. So the weights for EMA will be (for N+1 examples): $\alpha, \alpha \cdot \gamma, \alpha \cdot \gamma^2, ..., \alpha \cdot \gamma ^ {N-1}, \gamma ^ N$. All these weights sums to $1$ for all $N>0$. So the correct code for plotting the weights is:

num_timesteps = 1000
x = np.linspace(0, num_timesteps, num_timesteps+1)
for decay in decay_list:
    y = (decay**x)
    y[:-1] *= 1-decay
    assert abs(y.sum()-1) < 1e-6, "weights (y) should sum to 1."
    plt.plot(x, y, label=f'{decay}')

With the above code, we get the following plots

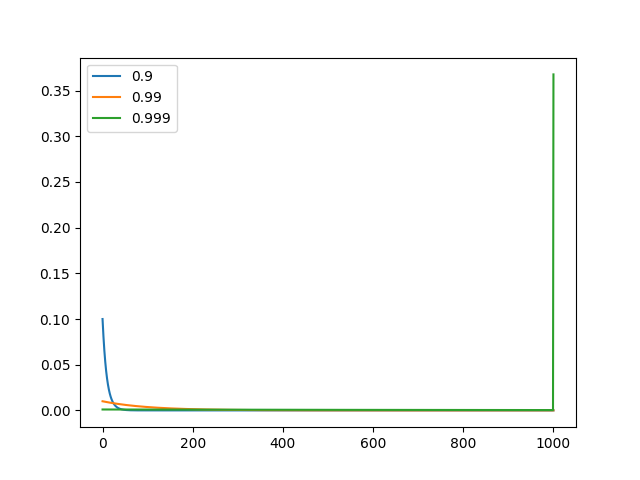
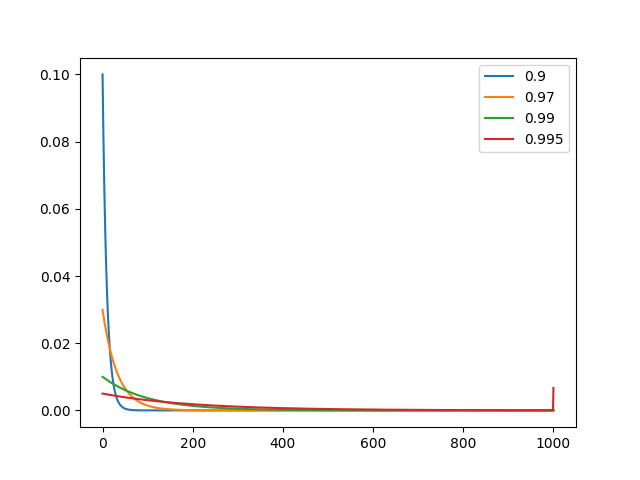
As can be seen from the first plot, even a decay rate of 0.999 gives a very high weight to the first example seen by EMANorm. We can also check that if decay = 1, then all the weight is given to the first example, and all the subsequent examples are not given any weight (since alpha becomes 0). Therefore decay values extremely close to 1 are undesirable. This is the reason why the tests in #538 are failing since the default decay of 0.9997 is very high.

From the second plot, we can also see that decay rates close to or lesser than 0.9 are also not good since they give significantly lesser weight to previously seen examples. Therefore, weights in the range 0.97-0.992 seem reasonable for horizon lengths of 1000.

[taufeeque9]

For testing the correctness of EMANorm, I had earlier implemented Algorithm 1 from Incremental_batch_EMA_and_EMV.pdf in the class EMANormIncremental. However, since Algorithm 1 is numerically unstable, the test_ema_norm_batch_correctness fails for decay = 0.5 and num_samples = 1000 as shown by @yawen-d in #538. So I have now implemented Algorithm 2 in EMANormIncremental to test the implementation of Algorithm 3 used in EMANorm.

[yawen-d]

Thanks for the response! I would be happy to continue this discussion in this issue #540.

[AdamGleave]

Ah, I guess this error gets "canceled out" later on: the weights sum to 1/b not 1, so if we just change the 2nd step to be 1 - b*w_{m,m} then everything works out.

On Tue, 9 Aug 2022, 15:30 Adam Gleave, @.***> wrote:

Thanks for putting the PDF together Lev!

I don't follow the 2nd step in lemma 2, where the denominator switches from 1-alpha to 1-w_{m,m}. I thought w_{m,m} was alpha/b -- so wouldn't these only agree in the case b=1?

On Mon, 8 Aug 2022, 06:01 Lev McKinney, @.***> wrote:

@.**** commented on this pull request.

In src/imitation/util/networks.py https://github.com/HumanCompatibleAI/imitation/pull/522#discussion_r939804538 :

• def update_stats(self, batch: th.Tensor) -> None:

•    """Update `self.running_mean` and `self.running_var` in batch mode.
  

•    Args:
  

•        batch: A batch of data to use to update the running mean and variance.
  

•    """
  

•    b_size = batch.shape[0]
  

•    batch = batch.reshape(b_size, -1)
  

•    # Shuffle the batch since we don't don't want to bias the mean
  

•    # towards data that appears latter in the batch
  

•    perm = th.randperm(b_size)
  

•    batch = batch[perm]
  

•    # geometric progession of decay: decay^(N-1),...,decay,1
  

•    weights = th.vander(th.tensor([self.decay]), N=b_size).T
  

•    alpha = 1 - self.decay
  

•    if self.count == 0:
  

Coming back to this again I think I've finally figured out the correct incremental algorithm. I've attached in bellow with a proof of correctness,

Incremental EMA with batches.pdf https://github.com/HumanCompatibleAI/imitation/files/9278587/Incremental.EMA.with.batches.pdf

— Reply to this email directly, view it on GitHub https://github.com/HumanCompatibleAI/imitation/pull/522#discussion_r939804538, or unsubscribe https://github.com/notifications/unsubscribe-auth/AALZ3I4H4OGGVTGM7L3JO4LVYCBAJANCNFSM55ZGYWNA . You are receiving this because your review was requested.Message ID: @.***>