Fix TaylorMath

[Valchap]

I made a simple program to test speed of sin. The time is in nanosecond for 100 000 000 sin.

49568084775 JavaMath 19733161 LibGDXMath 2582929017 RandomMath 21765391 RivensFullMath 16946326 RivensHalfMath 23968648 RivensMath 5779427 TaylorMath 6101699 Fixed TaylorMath

TaylorMath is clearly faster but it work only for numbers between -2Pi and 2Pi so i fixed it.

It would be good for it to become the default algorithm.

[liach]

You can just add modulo of the wanted number by 2π.

[Valchap]

You're right I was thinking that it work only of integers.

[Valchap]

But it is ~100 time slower.

4781994442 nanoseconds

[liach]

So you might consider keeping both versions for best efficiency.

[DesWurstes]

I just noticed that Taylor's algorithm can be optimized to

		x -= x3 * 0.16666666666666666666666666666667;
		x += x5 * 0.00833333333333333333333333333333;
		//x -= x7 * 1.984126984126984126984126984127e-4;
		//x += x9 * 2.7557319223985890652557319223986e-6;
		//x -= x11 * 2.5052108385441718775052108385442e-8;
		//x += x13 * 1.6059043836821614599392377170155e-10;
		//x -= x15 * 7.6471637318198164759011319857881e-13;
		//x += x17 * 2.8114572543455207631989455830103e-15;

But it needs 18 if-elseif chain conditions, it's going to be worth it, I'll be much faster. I'll try to implement it this week. (I can't give a promise.)

[DesWurstes]

What's going on? (the cordic here is actually taylor optimized)

Am I doing something wrong while testing?

[Valchap]

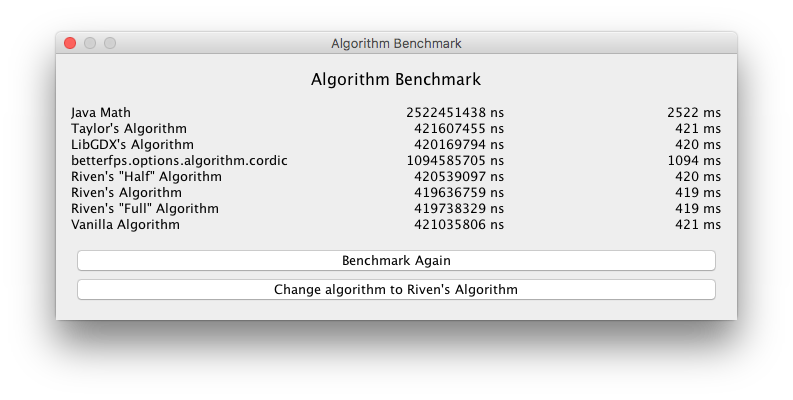
I also tested. It is the < comparator. It's very slow for double and float.

[DesWurstes]

Can't be, when I changed the code like this: https://hastebin.com/toderojofu.java It gives a similar result:

[Valchap]

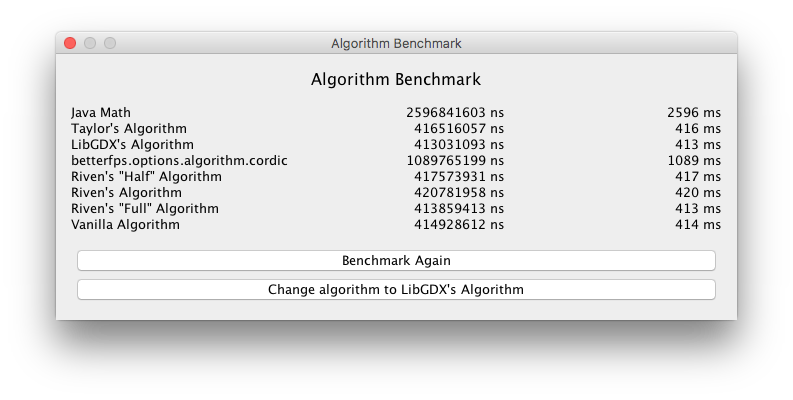
It's all conditions <, <=, >, >= are slow.