Add tangent-space option for r_showNormalMaps

[slipher]

It's kind of hard to interpret the colors produced by r_showNormalMaps, since you have to factor out the transformation from texture-based to absolute coordinates (assuming that's not the part of the calculation you're interested in), and then figure out how XYZ converts to RGB. So I tried to create a more intuitive version.

The colors are chosen according to the tangent space (i.e. relative to the texture) coordinates. The calculation uses HSL colors. The hue is according to the direction of the x and y components in the color wheel, the saturation in inversely proportional to z, and the lightness is constant. So we should have +x = red, -x = cyan, +y = green, -y = violet, +z = gray.

For a demonstration, see this button with outward-sloping edges from Parpax (/r_shownormalmaps 2, /testcgrade):

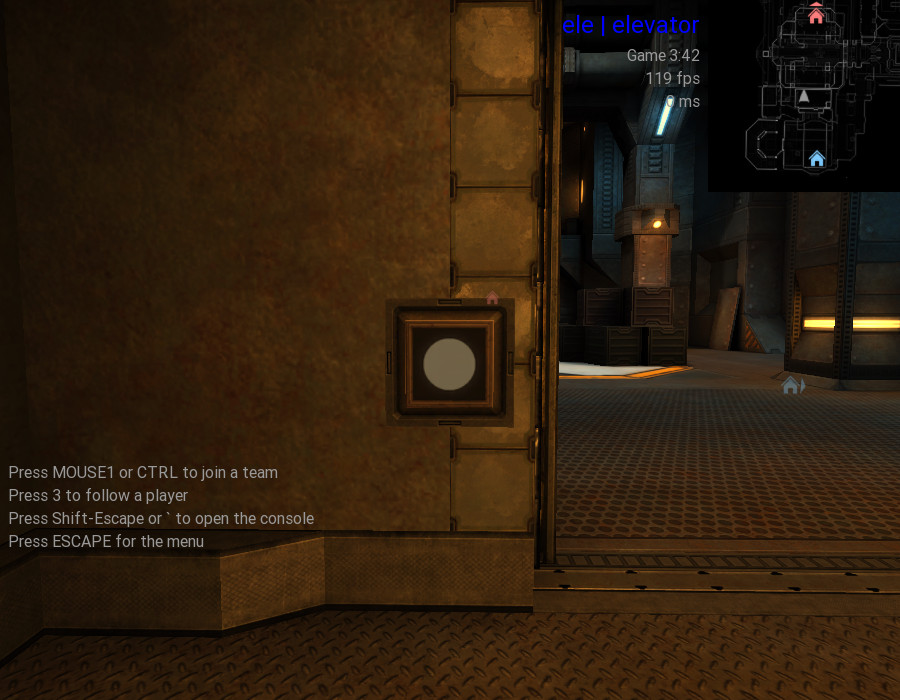
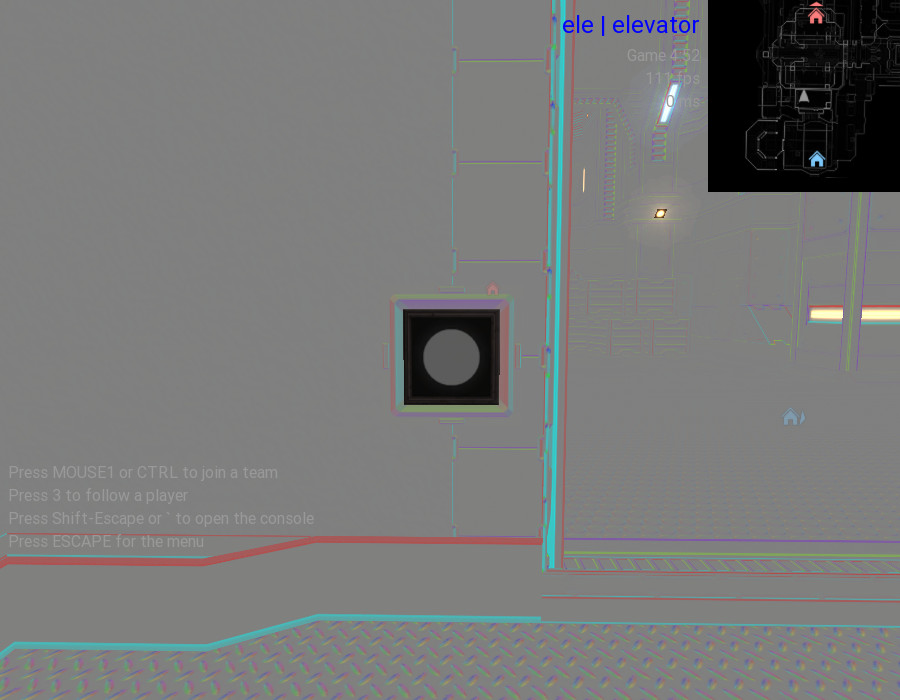
Things work as expected, except that the color wheel is flipped on the y-axis. @illwieckz I recall you've posted some things about different normalmap conventions... do you have any idea why this is? The OpenGL resources I checked say that +y should be upward, but the opposite is observed.

[illwieckz]

I'm not sure to understand what you are trying to do, but the commit I added in my branch there may help you: https://github.com/illwieckz/Daemon/commits/normalwheel

Basically it adds two more options for r_showNormalMaps:

0. no debug
1. world space: initial debug mode
2. computed tangent space: your compute
3. generated file: if Y transformation applies, it is applied, if generated from height map, it would be displayed there
4. raw file: as loaded before any optional transformation

raw file:

Note that your GLSL code does not compile on my end, I get that error:

Warn: Compile log:
0:198(38): error: syntax error, unexpected ')'

[illwieckz]

Things work as expected, except that the color wheel is flipped on the y-axis. @illwieckz I recall you've posted some things about different normalmap conventions... do you have any idea why this is? The OpenGL resources I checked say that +y should be upward, but the opposite is observed.

If you're watching a bump (not a hole), cyan must be on the bottom, like if cyan light was going from the floor. OpenGL uses +X +Y +Z, definitely.

DirectX uses +X -Y +Z which feels more natural when looking at normal map files as cyan light seems to come from the sky, which makes easy to imagine what it is representing.

[illwieckz]

You can find my latest build of the test-normal map there: https://dl.illwieckz.net/b/unvanquished/test-assets/

Some screenshots:

[illwieckz]

Note that you can reset normal scaling (inverting) by setting r_normalScale to 0, whatever the debug mode. This is currently an unsupported feature, but I think I will make it officially supported:

[slipher]

So I expected the coordinate system for normals to be like this:

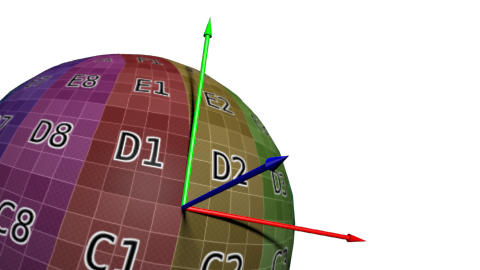
But the y-axis (green) actually points in the opposite direction, giving us (against convention) a left-handed coordinate system. (Note that the fact that in r_showNormalMaps 2, +x is supposed to be red and +y is supposed to be green, is a coincidence. The HSL color wheel is arbitrary.)

I believe it looks like this is because the coordinate system is based on normal, tangent, and binormal vectors. The binormal is defined as the cross product of the tangent and normal. So if you put the axes in the order (tangent, binormal, normal) you will get a left-handed coordinate space.

One mysterious fact is that in QTangentToLocalBasis (vertexSimple_vp.glsl) it uses a technique described here:

To calculate the bitangent, we take the cross product of the normal and tangent vectors then multiply it by a constant in tangent.w which is the handedness of the tangent space.

Unfortunately the article does not explain why you would want the handedness of the coordinate system to be "configurable".

I wonder how much trouble it would to convert things to the seemingly more standard tangent/bitangent/normal basis? The term "binormal" is senseless since it is actually a tangent vector to the surface.