regular 2D hyperbolic polygons using the poincaré disk model

[Hjagu09]

Hyperbolic geometry is an type of non-Euclidian geometry which I would love to see an coding train video on. Hyperbolic geometry is defined as this on the Wikipedia page:

hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R.

Basically, for any line there can be a lot of different parallels to one line, like this (note that this are all straight lines)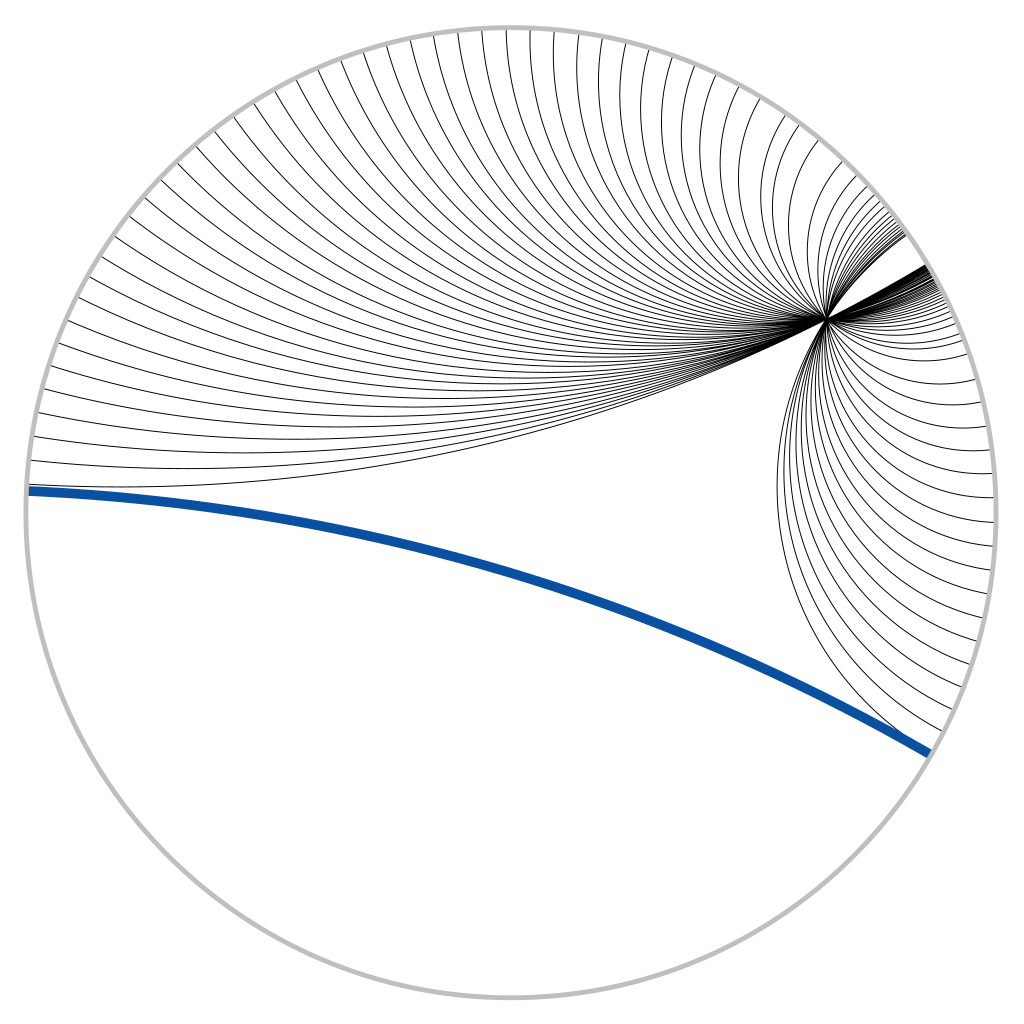

---

The most common way of projecting hyperbolic space is using the poincaré disk model. All images I shown here uses this model. It projects the entire hyperbolic space on to an disk and it's most notable popertys are:

The distance from the center of the disk to the edge is infinite

straight lines consist of arcs of Euclidean circles contained within the disk that are orthogonal to the boundary of the disk, plus all diameters of the disk.

Challenge

Given any p and q were (p - 2) • (q - 2) > 4 render regular hyperbolic polygons with p vertices and q polygons adjacent to each vertex using the poincaré disk model.

---

The above image is an solution for p=3 q=12 For an complete solution, check out this page

Resources

• Verasrium (yt): parallel lines and hyperbolic/spherical geometry
• CodeParade (yt): explanation of hyperbolic geometry
• Malin Christersson: non Euclidian geometry and the Poincaré disk model (with interactive example)
• numberphile (yt): sports in hyperbolic geometry and part two
• "Rendering Non-Euclidean Geometry in Real-Time Using Spherical and Hyperbolic Trigonometry" by Prof Yang-Hui He, Dr Chris Child and Daniil Osudin
• Poincaré disk model Wikipedia page
• hyperbolic geometry Wikipedia page

---