Possibility for complex calculations?

[Zaq-Xander]

Just putting this out there, too:

It'd be cool to have the opportunity for complex-valued inputs and outputs to go through the application.

In this project (https://www.math3d.org/iI0ydAfV) I've tried to create (x+iy)^2 as an explicit surface. The height denotes the real part of the expression and the colour denotes the imaginary part.

I'd propose having a separate 'complex mode' with functionality limited to creating such graphs (and other relevant functionality). In this complex mode, you could use the letter "i" to denote the imaginary unit rather than the unit vector in the x direction, and you could create functions that take in values on the horizontal input complex plane and graph their output using height and colour as in the thing I created (you could maybe have separate options for {height = real part of output, colour = imaginary part of output} and {height = magnitude of output, colour = argument of output}).

I think this could be a cool extension upon what's been provided so far :)

Thank you :)

[selfdual-brain]

I wanted to add an upvote for such feature from my side as well !

Complex mode would be great. By a "complex mode" I mean the ability to define function such as f(z)=1/z or f(z)=sin(z^2). Plus of course the ability to use Re() and Im() in expressions.

3D space can be used to naturally visualize functions ℂ→ℝ (which leads to a surface) and ℝ→ℂ (which leads to a curve in 3D by obviously assuming that X-axis represents the domain and for every point x∊X we draw a point on the plane othogonal to X-axis, passing via x).

We can even push the latter idea forward by visualising ℂ→ℂ functions in a way that is looks like a movie of morhping a curve in 3-dimensional space. In this movie, any still frame is just looking at f cut to the sub-domain defined with the equatin Im(z)=m - where parameter "m" is the still frame timepoint within the movie. For timepoint m, our parametric curve will represent f cut to the Im(z)=m line.

I actually made a couple of examples to show this technique. Please notice how much one have to struggle with making such examples - the struggle comes from the fact that the "complex mode" of calculation is missing. To see the "movie" please use the "m" slider. Best is to start m auto mode, and - while the movie is playing - rotate the space manually to understand the structure.

The examples are here: https://www.math3d.org/tQnRbqaQ

[ChristopherChudzicki]

Current Status

I just added the functions re, im, arg, and conj. Existing functions like sin and exp should already work with complex numbers. The imaginary unit is I (not i, which is [1,0,0], as you've noticed).

Examples:

• A surface https://www.math3d.org/M5TUOKD8
• @selfdual-brain Your curve visualization https://www.math3d.org/b0Pr53nn This is cool. I think perhaps I should add something like this to Examples pane on right hand side. @selfdual-brain any curves you're particularly fond of, or look particularly nice?

Future work

@Zaq-Xander @selfdual-brain Question for you both Does this achieve the functionality you are after, or do you think this is still too cumbersome / too much setup?

In terms of future work, one thing I could imagine would be for Explicit Surfaces to have an option (in the gear settings)... a toggle switch that if activated sets Z = X + I Y:

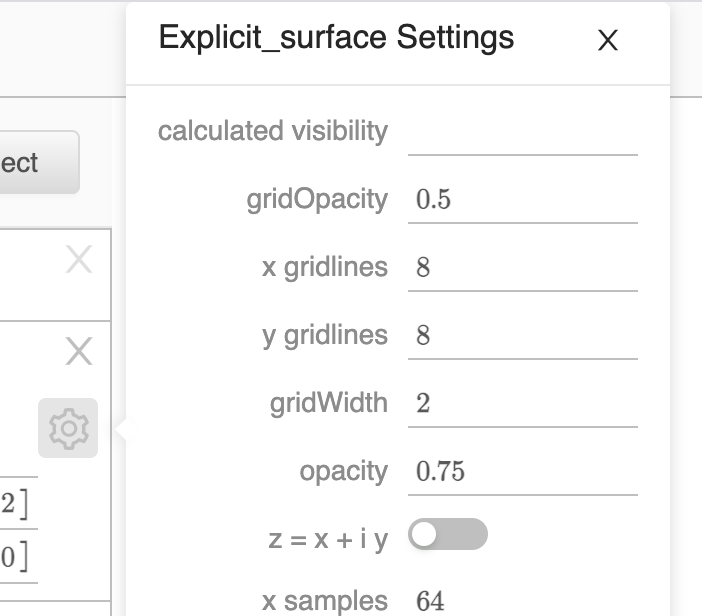
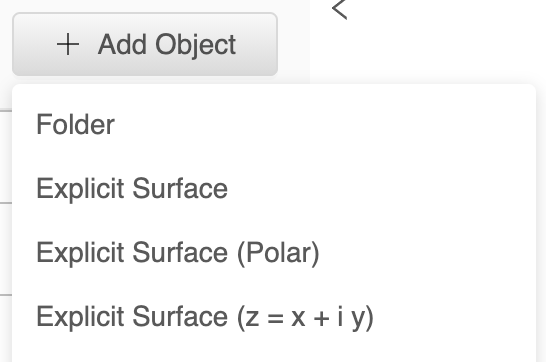
Or even a new object type:

[selfdual-brain]

Wow ! This works great. Thank you a lot for your hard work, Christopher. So far the new functionality fulfills my expectations in 100% (as far as I can say after 1 hour of playing around). This is really a cool upgrade.

Your idea to add "z=x+Iy" in the gear menu is also pretty cool. I am just only a little worried aren't we now running into collision of variables ? Because "z" is already used for the third axis. I can imagine this may confuse users. Also this may become a problem with implicit surfaces (where variable z is normally used and means something else).

Also I came up with an alternative idea: how about adding a dedicated object type named "Explicit surface (complex domain)", where the conventions work differently: variables x and y are NOT recognized by the parser, instead only the variable z is recognized, and the plotter assumes XY plane to be the complex domain. In other words, the "Explicit surface (complex domain)" would work only with functions ℂ→ℝ defined with only one variable z. Maybe this will be more easy to grasp by users than the extra option in the gear menu ?

[Zaq-Xander]

To preface this post, I've put most of my feedback in the following math3d document: https://www.math3d.org/BVg2gwWc. The stuff on this post is just paragraphs that I felt were better typed-out here.

I agree with the last paragraph suggestion that @selfdual-brain provided. Having explicitly "Explicit surface (complex domain)" for functions ℂ→ℝ would work really nicely. I agree with having the parser accept only z for that (similar to how only t is accepted by the parametric curve). (Unrelated note, but I'd personally recommend being able to change the designated variables for each object type. This could allow users to change the variables used if it conflicts with any function/variable definitions they've made with the "Variable or Function" and "Variable Slider" objects. I'll put this suggestion in a separate issue if I remember to do so.) I'd like to add to the "Explicit surface (complex domain)" suggestion: rather than having the bounds read "x ∈ [x_1 , x_2]" and "y ∈ [y_1 , y_2]", these should instead read "re(z) ∈ [x_1 , x_2]" and "im(z) ∈ [y_1 , y_2]".

Moreover, to add to the "Explicit surface (complex domain)" suggestion, we could have that when "f(z)" is input, it automatically graphs "re(f(z))" on the vertical axis and it sets the colour map to "im(f(z))". Although you can do this manually (set the input to "re(f(z))" and the colour map to "im(f(z))") with the changes currently proposed, this would be a simple quality of life change for users. Then, in the gear settings menu, you could have a switch which changes it to graphing abs(f(z)) on the vertical axis and arg(f(z)) on the colour map (again, this can be done manually, but it'd be a quality of life change).

If we're going to have an object type for functions ℂ→ℝ, it'd also be nice to get an object type for functions ℝ→ℂ. Perhaps you could call this object type "Explicit curve (complex codomain)". For a function f:ℝ→ℂ, this object type would follow the same process as currently implementing a "Parametric Curve" with the input [t, re(f(t)), im(f(t))] (or if you'd prefer the input on the vertical axis, [re(f(t)), im(f(t)), t)]). This is still manually possible, but it'd be another quality of life change.

There's a bunch more feedback that I have after playing around for an hour or so, but rather than weigh down a long comment with lots of text, I've typed it into a math3d document. Here's the link to my feedback: https://www.math3d.org/BVg2gwWc

While I was making this feedback, I got curious and made a demonstration of the Cauchy-Riemann equations (the link for which I've pasted in the above math3d document also). I'll re-paste the link here in case you'd like to use this for whatever purpose: https://www.math3d.org/cR9ISOti

That's all I have to say! Thank you so much for providing and updating an already-awesome tool :)

[Zaq-Xander]

Just to add, you may like to implement cis which would simply be the calculation cis(t) = exp(I*t) = cos(t) + I*sin(t). It's not important to me personally, but I know that many people prefer to use it.