blog-frontend 懂得都懂 —

懂得都懂 —— 堆

Open Caaalabash opened this issue 4 years ago • 1 comments

1. 关于堆的算法知识

堆是一个数组，它可以被看成一个近似的完全二叉树，树上的每一个节点对应数组的一个元素。除了最底层外，该树是完全充满的，而且是从左向右填充。 -- 算法导论

堆分为：

大顶堆：每个非根节点的值都不大于其父节点
小顶堆：每个非根节点的值都不小于其父节点

堆常见操作：

heapify: 把一个乱序的数组变成堆结构的数组，时间复杂度为O(n)
push: 把一个数值添加进堆结构，并保持堆结构，时间复杂度为O(log n)
pop: 去除根节点，并保持堆结构，时间复杂度O(log n)
sort: 堆排序，时间复杂度O(nlog n)，空间复杂度O(1)

父节点与左右节点的索引关系如图：

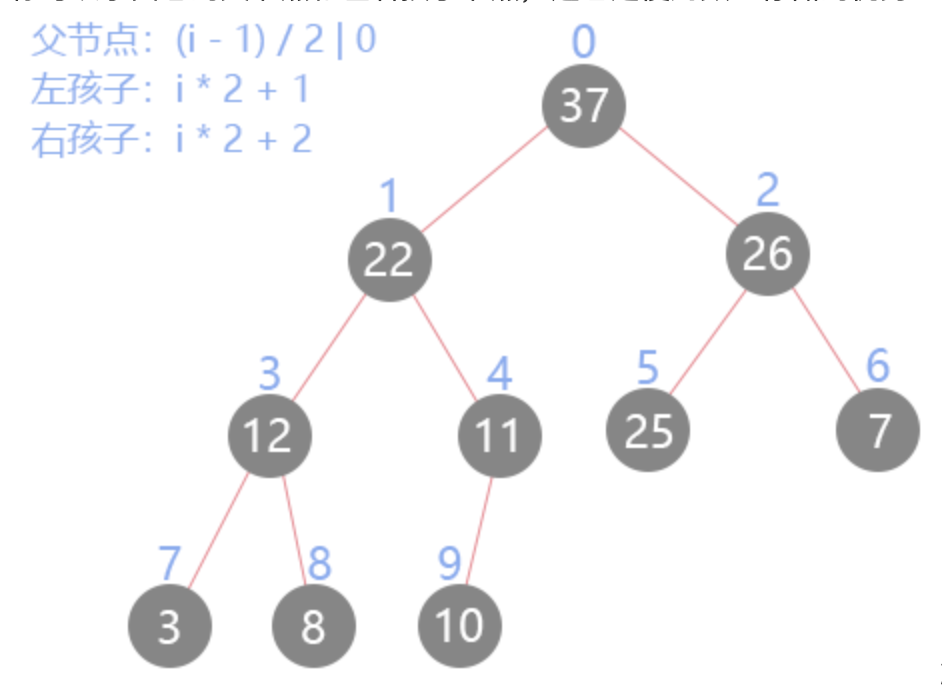
父节点与左右节点的索引关系

为什么快速排序要比堆排序性能好：

堆排序数据访问的方式没有快速排序友好：快速排序顺序访问，堆排序跳着访问，对CPU缓存是不友好的
对于同样的数据，排序过程中，堆排序算法的数据交换次数要多于快速排序

关于堆排序：

原地排序算法
不稳定排序算法
时间复杂度O (nlog n)

1.1 交换操作(swap)

交换操作：通常用于交换父子节点或者首尾节点

function swap(arr, i, j) {
  [arr[i], arr[j]] = [arr[j], arr[i]]
}

1.2 比较操作(less)

比较操作：确定大顶堆还是小顶堆，虽然常见的命名是less，但并不是小于符号的意思。

function less(a, b) {
  return a > b
}

1.3 push会用到的上浮(siftUp)操作

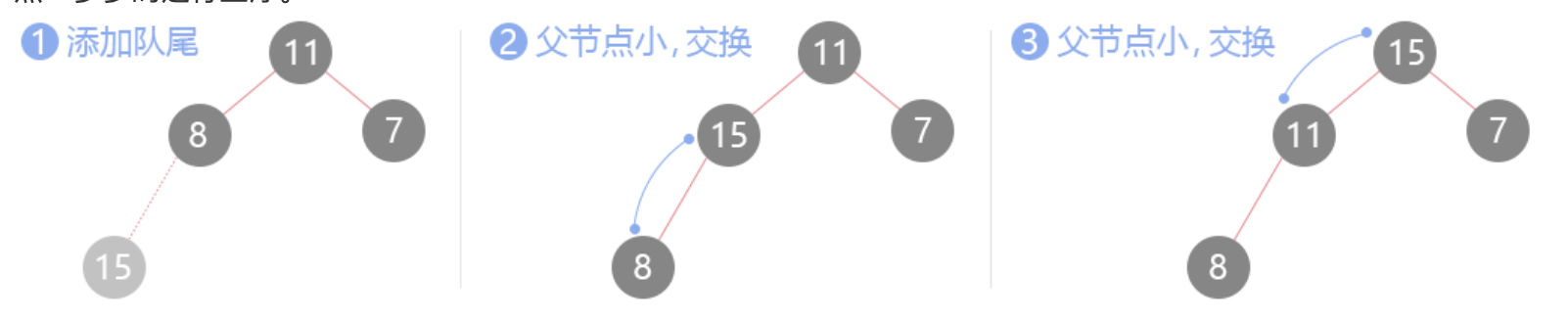
push往堆里添加任意元素而又不能破坏堆的性质，步骤如下：

首先将添加的元素推入堆数组的末尾，然后进行上浮操作
末尾节点与其父节点比较，如果满足less(当前节点值, 父节点值)，则交换
重复这个过程

push会用到的上浮(siftUp)操作

function push(arr, v) {
  arr.push(v)
  siftUp(arr, arr.length - 1)
}

function siftUp(arr, i) {
  const parentIndex = (i - 1) / 2 | 0
  if (less(arr[i], arr[parentIndex])) {
    swap(arr, i, parentIndex)
    siftUp(arr, parentIndex)
  }  
}

上方代码使用递归，感觉比 while 循环更好理解，逻辑就是这么个逻辑。

1.4 pop会用到的下沉(siftDown)操作

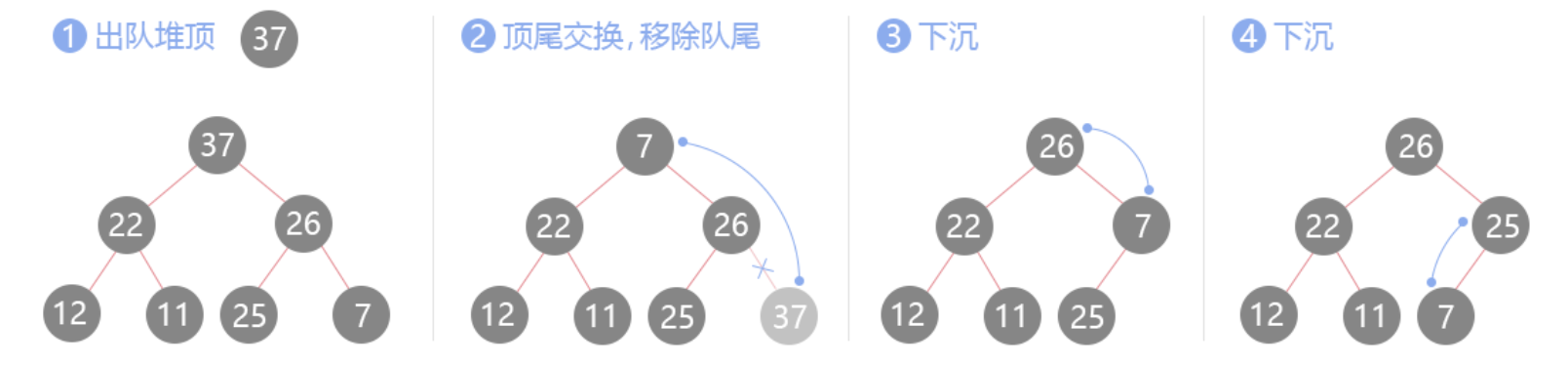
pop删除根节点而又不能破坏堆的性质，步骤如下：

将数组第一个元素删除，将数组的最后一个元素放在堆顶，然后进行下沉操作
将堆顶元素与左右孩子比较，与其中最大(小)值的孩子交换位置
重复这个过程

pop会用到的下沉(siftDown)操作

function pop(arr) {
  if (arr.length === 0) {
    return  
  }
  swap(arr, 0, arr.length - 1)
  const popItem = arr.pop()
  siftDown(arr, 0, arr.length - 1)
  return popItem
}

// 这个length参数排序时有用
function siftDown(arr, i, length) {
  let leftIndex = i * 2 + 1
  if (leftIndex >= length) {
    return
  }
  if (leftIndex + 1 < length && less(arr[leftIndex + 1], arr[leftIndex])) {
    leftIndex++
  }
  if (less(arr[leftIndex], arr[i])) {
    swap(arr, leftIndex, i)
    siftDown(arr, leftIndex, length)
  }
}

1.5 堆化操作(heapify)与堆排序(heapSort)操作

对一个初始数组进行堆化操作：以最后一个叶子节点的父节点为起点，把起点到根节点之间的所有节点进行下沉操作

function heapify(arr) {
  for (let last = (arr.length - 2) / 2 | 0; last >= 0; last--) {
    siftDown(arr, last, arr.length)
  }
}

假设此处得到一个大顶堆，排序操作如下：

将最大值(索引0)与最后一个元素交换，这样就在索引 i 固定了最大值
进行下沉操作（此处缩小了下沉的范围，就不会影响到索引 i
重复这样的操作

function heapSort(arr) {
  heapify(arr)
  for (let i = arr.length - 1; i > 0; i--) {
    swap(arr, 0, i)
    siftDown(arr, 0, i)
  }
}

1.6 实现

组合一下代码即可：

function less(a, b) {
  return a > b
}
function swap(arr, i, j) {
  [arr[i], arr[j]] = [arr[j], arr[i]]
}
function push(arr, v) {
  arr.push(v)
  siftUp(arr, arr.length - 1)
}
function siftUp(arr, i) {
  const parentIndex = (i - 1) / 2 | 0
  if (less(arr[i], arr[parentIndex])) {
    swap(arr, i, parentIndex)
    siftUp(arr, parentIndex)
  }  
}
function pop(arr) {
  if (arr.length === 0) {
    return  
  }
  swap(arr, 0, arr.length - 1)
  const popItem = arr.pop()
  siftDown(arr, 0, arr.length - 1)
  return popItem
}
function siftDown(arr, i, length) {
  let leftIndex = i * 2 + 1
  if (leftIndex >= length) {
    return
  }
  if (leftIndex + 1 < length && less(arr[leftIndex + 1], arr[leftIndex])) {
    leftIndex++
  }
  if (less(arr[leftIndex], arr[i])) {
    swap(arr, leftIndex, i)
    siftDown(arr, leftIndex, length)
  }
}
function heapify(arr) {
  for (let last = (arr.length - 2) / 2 | 0; last >= 0; last--) {
    siftDown(arr, last, arr.length)
  }
}
function heapSort(arr) {
  heapify(arr)
  for (let i = arr.length - 1; i > 0; i--) {
    swap(arr, 0, i)
    siftDown(arr, 0, i)
  }
}

2. 堆的实际应用一: 利用堆求中位数

对于一组静态数据，中位数是固定的，我们可以先排序，第 n/2 个数据就是中位数。每次询问中位数的时候，我们直接返回这个固定的值就好了。所以，尽管排序的代价比较大，但是边际成本会很小。但是，如果我们面对的是动态数据集合，中位数在不停地变动，如果再用先排序的方法，每次询问中位数的时候，都要先进行排序，那效率就不高了。

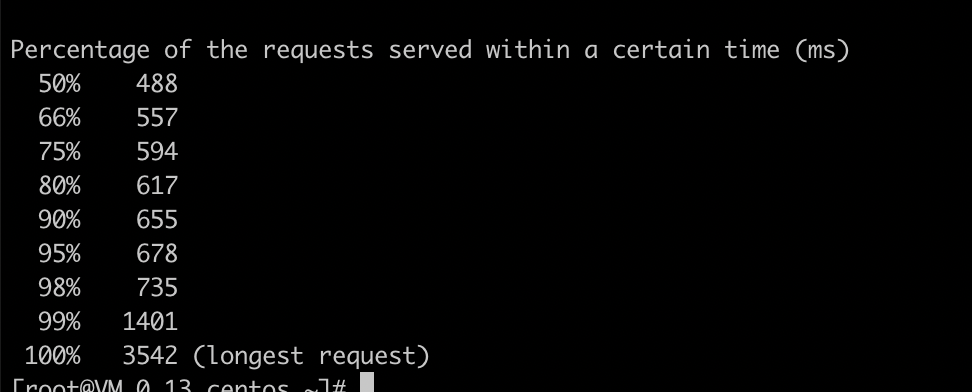
抛出一个压力测试的实例：下图中的P99、P50等数据是如何得出的？显然是堆

我们维护两个堆，一个大顶堆，一个小顶堆，大定堆中保存 n * 99% 个数据，小顶堆中保存 n * 1% 个数据。大顶堆堆顶的数据就是我们要找的P99响应时间。

压力测试

2.1 leetcode295 - 数据流中的中位数

步骤：

两个堆
- 用于存储较小一半数字的最大堆lo
- 用于存储较大一半数字的最小堆hi
- 最大堆存储的元素最多比最小堆多一个，假设接受到K个数据
  - k = 2n: 每个堆都包含 n 个元素，中间值可以从两个堆的堆顶计算出
  - k = 2n+1: 最大堆 n+1 个，中间值为最大堆的堆顶
push一个数num, 此时最大堆、最小堆数量可能失衡，将会有两种操作：
- 从lo中移除最大的元素并将其提供给hi
- 从hi中移除最小的元素并将其提供给lo

Golang题解：

package problem0295

type MedianFinder struct {
	max []int
	min []int
}

func Constructor() MedianFinder {
	return MedianFinder{
		max: []int{},
		min: []int{},
	}
}

func (this *MedianFinder) AddNum(num int) {
	if len(this.max) > len(this.min) {
		if num > this.max[0] {
			this.min = append(this.min, num)
			up(this.min, len(this.min)-1, smaller)
		} else {
			this.min = append(this.min, this.max[0])
			up(this.min, len(this.min)-1, smaller)
			this.max[0] = num
			down(this.max, 0, bigger)
		}
	} else {
		if len(this.min) != 0 && num > this.min[0] {
			this.max = append(this.max, this.min[0])
			up(this.max, len(this.max)-1, bigger)
			this.min[0] = num
			down(this.min, 0, smaller)
		} else {
			this.max = append(this.max, num)
			up(this.max, len(this.max)-1, bigger)
		}
	}
}

func (this *MedianFinder) FindMedian() float64 {
	if len(this.max) == len(this.min) {
		return float64(this.max[0]+this.min[0]) / 2
	}
	return float64(this.max[0])
}

// 针对性的堆操作实现
type compareFunc func(i, j int) bool

func up(arr []int, i int, less compareFunc) {
	pIndex := (i - 1) / 2
	if less(arr[i], arr[pIndex]) {
		swap(arr, i, pIndex)
		up(arr, pIndex, less)
	}
}
func down(arr []int, i int, less compareFunc) {
	leftIndex := i*2 + 1
	if leftIndex >= len(arr) {
		return
	}
	if leftIndex+1 < len(arr) && less(arr[leftIndex+1], arr[leftIndex]) {
		leftIndex++
	}
	if less(arr[leftIndex], arr[i]) {
		swap(arr, i, leftIndex)
		down(arr, leftIndex, less)
	}
}
func bigger(i, j int) bool {
	return i > j
}
func smaller(i, j int) bool {
	return i < j
}
func swap(arr []int, i, j int) {
	arr[i], arr[j] = arr[j], arr[i]
}

3. 堆的实际应用二: 高性能定时器

假设我们有一个定时器，定时器中维护了很多定时任务，每个任务都设定了一个要触发执行的时间点。定时器每过一个很小的单位时间（比如 1 秒），就扫描一遍任务，看是否有任务到达设定的执行时间。如果到达了，就拿出来执行。

但是，这样每过 1 秒就扫描一遍任务列表的做法比较低效，主要原因有两点：第一，任务的约定执行时间离当前时间可能还有很久，这样前面很多次扫描其实都是徒劳的；第二，每次都要扫描整个任务列表，如果任务列表很大的话，势必会比较耗时。

更好的解决办法当然是堆：

我们按照任务设定的执行时间，将这些任务存储在优先级队列中，队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务。这样，定时器就不需要每隔 1 秒就扫描一遍任务列表了。它拿队首任务的执行时间点，与当前时间点相减，得到一个时间间隔 T。这个时间间隔 T 就是，从当前时间开始，需要等待多久，才会有第一个任务需要被执行。这样，定时器就可以设定在 T 秒之后，再来执行任务。从当前时间点到（T-1）秒这段时间里，定时器都不需要做任何事情。

3.1 Nodejs 14 的 setTimeout 实现

起点位于lib/timers中setTimeoout函数：

function setTimeout(callback, after) {
  const timeout = new Timeout(callback, after);
  insert(timeout, timeout._idleTimeout);

  return timeout;
}

lib/internal/timers中Timeout构造函数和insert函数

function Timeout(callback, after) {
  this._idleTimeout = after;
  this._idleStart = null;
}

function insert(item, msecs, start = getLibuvNow()) {
  // 记录定时器的开始时间
  item._idleStart = start;
  // 该延迟时间是否已经存在对应的链表
  let list = timerListMap[msecs];
  // 不存在链表
  if (list === undefined) {
    // 开始时间 + 延迟时间 = 到期时间
    const expiry = start + msecs;
    // 为这个延迟时间创建一个链表
    timerListMap[msecs] = list = new TimersList(expiry, msecs);
    // 将这个链表插入小顶堆（优先队列）
    timerListQueue.insert(list);
    // nextExpiry是全局变量，初始值 Infinity，含义是最快到期时间
    // 如果当前到期时间(expiry)比全局记录的最快到期时间(nextExpiry)还要早，调用scheduleTimer函数
    if (nextExpiry > expiry) {
      // 进入c++的世界
      scheduleTimer(msecs);
      nextExpiry = expiry;
    }
  }
  // 添加进链表
  L.append(list, item);
}

然后就是 c++ 的 scheduleTimer函数，看不懂也关系，我也看不懂。

总之作用就是：c++层面开启一个计时器，会在事件循环的 timer 阶段判断是否过期，是的话执行RunTimers函数

void ScheduleTimer(const FunctionCallbackInfo<Value>& args) {
  auto env = Environment::GetCurrent(args);
  env->ScheduleTimer(args[0]->IntegerValue(env->context()).FromJust());
}

void Environment::ScheduleTimer(int64_t duration_ms) {
  if (started_cleanup_) return;
  uv_timer_start(timer_handle(), RunTimers, duration_ms, 0);
}

nodejs在初始化时对定时器进行了初始化工作，lib/internal/bootstrap/node.js

{
  const { getTimerCallbacks } = require('internal/timers');
  const { setupTimers } = internalBinding('timers');
  const { processImmediate, processTimers } = getTimerCallbacks(runNextTicks);
  // Sets two per-Environment callbacks that will be run from libuv:
  // - processImmediate will be run in the callback of the per-Environment
  //   check handle.
  // - processTimers will be run in the callback of the per-Environment timer.
  setupTimers(processImmediate, processTimers);
}

快结束了，接下来看internal/timer.js中的processTimers就好了

  function processTimers(now) {
    nextExpiry = Infinity;

    let list;
    let ranAtLeastOneList = false;
    // 从小顶堆中取出根节点，即最快到期的节点
    while (list = timerListQueue.peek()) {
      // 还没过期
      if (list.expiry > now) {
        nextExpiry = list.expiry;
        return refCount > 0 ? nextExpiry : -nextExpiry;
      }
      // list是具有相同过期时间的链表
      listOnTimeout(list, now);
    }
    return 0;
  }
  function listOnTimeout(list, now) {
    const msecs = list.msecs;
    let ranAtLeastOneTimer = false;
    let timer;
    // 遍历这个链表
    while (timer = L.peek(list)) {
      // 计算已经过去的时间
      const diff = now - timer._idleStart;

      // 过去的时间比延迟时间小，说明没过期
      if (diff < msecs) {
        // 调整到期时间
        list.expiry = MathMax(timer._idleStart + msecs, now + 1);
        list.id = timerListId++;
        // 调整到期时间后，下沉处理
        timerListQueue.percolateDown(1);
        return;
      }
      // 移除这个节点
      L.remove(timer);
      // 执行timer的_onTimeout回调
      try {
        const args = timer._timerArgs;
        if (args === undefined)
          timer._onTimeout();
        else
          timer._onTimeout(...args);
      } finally {
        // 省略  
      }
    }
    // 为空则删除
    if (list === timerListMap[msecs]) {
      delete timerListMap[msecs];
      timerListQueue.shift();
    }
  }

4. 堆的实际应用三: 求Top K

实际例子比如："如何快速获取到Top 10最热门搜索关键字", 具体看leetcode一道题就成了

4.1 leetcode373 - 查找和最小的k对数字

这事见得多了，我只想说懂得都懂，不懂的我也不多解释，自己知道就好，细细品吧。你们也别来问我怎么了，利益牵扯太大，说了对你我都没好处，当不知道就行了，其余的我只能说这里面水很深，牵扯到很多东西。详细情况你们自己是很难找的，网上大部分已经删除干净了，所以我只能说懂得都懂。

func kSmallestPairs(nums1 []int, nums2 []int, k int) [][]int {
	heap := make([][]int, 0)
	for _, a := range nums1 {
		for _, b := range nums2 {
			if len(heap) < k {
				push(&heap, []int{a, b})
			} else if less(heap[0], []int{a, b}) {
				pop(&heap)
				push(&heap, []int{a, b})
			}
		}
	}
	return heap
}

func push(arr *[][]int, x []int) {
	*arr = append(*arr, x)
	siftUp(*arr, len(*arr)-1)
}

func pop(arr *[][]int) {
	lastIndex := len(*arr) - 1
	swap(*arr, 0, lastIndex)
	siftDown(*arr, 0, lastIndex)
	*arr = (*arr)[0:lastIndex]
}

func siftDown(arr [][]int, i int, length int) {
	leftIndex := i*2 + 1
	if leftIndex >= length {
		return
	}
	if leftIndex+1 < length && less(arr[leftIndex+1], arr[leftIndex]) {
		leftIndex++
	}
	if less(arr[leftIndex], arr[i]) {
		swap(arr, leftIndex, i)
		siftDown(arr, leftIndex, length)
	}
}

func siftUp(arr [][]int, i int) {
	pIndex := (i - 1) / 2
	if less(arr[i], arr[pIndex]) {
		swap(arr, pIndex, i)
		siftUp(arr, pIndex)
	}
}

func less(a []int, b []int) bool {
	return a[0]+a[1] > b[0]+b[1]
}

func swap(arr [][]int, i int, j int) {
	arr[i], arr[j] = arr[j], arr[i]
}

参考

极客时间 - 堆的应用：如何快速获取到Top 10最热门的搜索关键词？

nodejs 14.0.0源码分析之setTimeout

Oct 21 '20 07:10 Caaalabash

牛批就完了

Oct 21 '20 07:10 wuweijia

blog-frontend blog-frontend copied to clipboard

懂得都懂 —— 堆

1. 关于堆的算法知识

1.1 交换操作(swap)

1.2 比较操作(less)

1.3 push会用到的上浮(siftUp)操作

1.4 pop会用到的下沉(siftDown)操作

1.5 堆化操作(heapify)与堆排序(heapSort)操作

1.6 实现

2. 堆的实际应用一: 利用堆求中位数

2.1 leetcode295 - 数据流中的中位数

3. 堆的实际应用二: 高性能定时器

3.1 Nodejs 14 的 setTimeout 实现

4. 堆的实际应用三: 求Top K

4.1 leetcode373 - 查找和最小的k对数字

参考

blog-frontend
blog-frontend copied to clipboard