cgal icon indicating copy to clipboard operation
cgal copied to clipboard
verified publisher icon CGAL

Representation of sets in the documentation.

Open albert-github opened this issue 4 years ago • 4 comments

In the output:Snap_rounding_2/group__PkgSnapRounding2Ref.html we see for the representation of a finite collection S of segments in the plane in the documentation:

image

a bit further down we see:

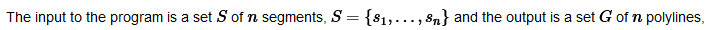
image

I'm not sure whether both S have the same meaning, if so I think:

  • either the term set or collection should be used
  • the representation of both S should happen in a similar way
  • probably the representation of G should be in the same style as chosen for the S.

I think these points should be investigated.

This issue is also related to proposed pull request #5715 (and #5707). For points we saws some misrepresentation in #5706

albert-github avatar May 16 '21 09:05 albert-github

I'm missing some information, but let me also add some.

  1. The "2D Arrangement" package has been revamped as part of a new feature; see Features/Arrangement on surface 2 https://cgal.geometryfactory.com/CGAL/Members/wiki/Features/Arrangement_on_surface_2 . For the new documentation see Documentation http://www.cs.tau.ac.il/~efif/doc_output4/Arrangement_on_surface_2/. This feature has been accepted (very) recently. If you think there is a discrepancy in the new doc, I would like to know.
  2. In the documentation (and in all publications) I always use calligraphic letters to denote sets (and non-calligraphic letters to denote entities that are not sets). Again, If you think there is a discrepancy, I would like to know.
  3. I haven't looked at the Snaprounding manual for quite some time and I wouldn't be surprised to see mistakes or inaccuracies there.
  • What do you refer to by "both S"? There is a set of segments S (which I would change to calligraphic S) and a set of polylines G (which I would change to calligraphic G).
    /_____/) o /_________ __ // (____ ( ( ( (/ (/-(-'_(/ _/

On Sun, 16 May 2021 at 12:32, albert-github @.***> wrote:

In the output:Snap_rounding_2/group__PkgSnapRounding2Ref.html we see for the representation of a finite collection S of segments in the plane in the documentation:

[image: image] https://user-images.githubusercontent.com/5223533/118392366-ad311c00-b639-11eb-8f38-c2821566fa80.png

a bit further down we see:

[image: image] https://user-images.githubusercontent.com/5223533/118392387-cf2a9e80-b639-11eb-9214-d7367291dea7.png

I'm not sure whether both S have the same meaning, if so I think:

  • either the term set or collection should be used
  • the representation of both S should happen in a similar way
  • probably the representation of G should be in the same style as chosen for the S.

I think these points should be investigated.

This issue is also related to proposed pull request #5715 https://github.com/CGAL/cgal/pull/5715 (and #5707 https://github.com/CGAL/cgal/issues/5707). For points we saws some misrepresentation in #5706 https://github.com/CGAL/cgal/issues/5706

— You are receiving this because you are subscribed to this thread. Reply to this email directly, view it on GitHub https://github.com/CGAL/cgal/issues/5716, or unsubscribe https://github.com/notifications/unsubscribe-auth/ABVBNODAHOJTIXNB3QK4ECTTN6GK5ANCNFSM446XSVVA .

efifogel avatar May 16 '21 10:05 efifogel

I wanted to look at the: https://cgal.geometryfactory.com/CGAL/Members/wiki/Features/Arrangement_on_surface_2 but I cannot access it wants me to login, but I have no login account for this.

I had a quick look at the (master build) files:

  • Arrangement_on_surface_2/group__PkgArrangementOnSurface2Ref.html
  • Arrangement_on_surface_2/index.html

And here I see that on some places \f$ \cal C\f$ is used and on other places: \f$ \mathcal{C}\f$.

A quick overview for \cal:

doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:Given a set \f$ \cal C\f$ of planar curves, the <I>arrangement</I>
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ \cal A(\cal C)\f$ is the subdivision of the plane into zero-dimensional,
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:one-dimensional and two-dimensional cells, called <I>vertices</I>, <I>edges</I> and <I>faces</I>, respectively induced by the curves in \f$ \cal C\f$.
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:The curves in \f$ \cal C\f$ can intersect each other (a single curve may also
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:We construct a collection \f$ \cal C''\f$ of
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:in two steps as follows. First, we decompose each curve in \f$ \cal C\f$
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:obtaining the collection \f$ \cal C'\f$. Note that an \f$ x\f$-monotone curve cannot
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:be self-intersecting. Then, we decompose each curve in \f$ \cal C'\f$ into
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:curve (or point) in \f$ \cal C'\f$. The collection \f$ \cal C''\f$ may also
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:contain isolated points, if the curves of \f$ \cal C\f$ contain such
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:points. The arrangement induced by the collection \f$ \cal C''\f$ can be
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ \cal A(\cal C) = \cal A(\cal C'')\f$. This graph can be represented using a
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:Given a set \f$ \cal C\f$ of unbounded curves, a simple approach for
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:representing the arrangement induced by \f$ \cal C\f$ would be to clip the
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ \cal C\f$. This process would result in a set \f$ \cal C\f$ of bounded curves
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:(line segments if \f$ \cal C\f$ contains lines and rays), and it would be
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:when one constructs an arrangement induced by a set \f$ \cal C\f$ of arbitrary
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:planar curves, she or he constructs a collection \f$ \cal C''\f$ of \f$ x\f$-monotone
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:subcurves of \f$ \cal C\f$ that are pairwise disjoint in their interior, and these
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:curves representing \f$ \cal C\f$, and by maintaining a cross-mapping between these
doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:planar subdivision induced by a set of input curves \f$ \cal C\f$.
doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:\f$ C \in \cal C\f$ - or may represent an overlap among several curves
doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:in \f$ \cal C\f$.
doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:representing \f$ \cal C\f$, and by maintaining a cross-mapping between these

and for \mathcal:

doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:An arrangement of intersecting line segments, as constructed in `global_insertion.cpp`. The segments of \f$ {\mathcal S}_1\f$ are drawn in solid lines and the segments of \f$ {\mathcal S}_2\f$ are drawn in dark dashed lines. Note that the segment \f$ s\f$ (light dashed line) overlaps one of the segments in \f$ {\mathcal S}_1\f$.
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ {\mathcal S}_1\f$ containing five line segments. Then we insert a single
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ {\mathcal S}_2\f$ with five more line segments in an aggregated fashion.
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:Notice that the line segments of \f$ {\mathcal S}_1\f$ are pairwise
doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ {\mathcal S}_2\f$ also contain pairwise interior-disjoint segments,
doc/Arrangement_on_surface_2/fig_src/ex_10.fig:4 0 0 50 -1 0 18 0.0000 2 270 2055 7262 4562 ${\\mathcal S}_2$\001
doc/Arrangement_on_surface_2/fig_src/ex_10.fig:4 0 1 50 -1 0 18 0.0000 2 270 2055 6282 4882 ${\\mathcal S}_1$\001
doc/Arrangement_on_surface_2/PackageDescription.txt:Given a set \f$ \mathcal{C}\f$ of planar curves, the <I>arrangement</I>
doc/Arrangement_on_surface_2/PackageDescription.txt:\f$ {\mathcal A}({\mathcal C})\f$ is the subdivision of the plane induced
doc/Arrangement_on_surface_2/PackageDescription.txt:by the curves in \f$ \mathcal{C}\f$ into maximally connected cells. The cells

So I think also here it would not hurt to make it consistent (and maybe through a macro).

On your questions:

  • what information are you missing?
  • The S in the 2 images of the issue are different.

albert-github avatar May 16 '21 10:05 albert-github

Absolutely. I've replaced \cal with \mathcal in this new branch I've mentioned (even though they cannot be visually distinguished).

Now I see the 2 'S' (so, all info is there) and you are correct, they should be identical and calligraphic.

/_____/) o /_________ __ // (____ ( ( ( (/ (/-(-'_(/ _/

On Sun, 16 May 2021 at 13:47, albert-github @.***> wrote:

I wanted to look at the: https://cgal.geometryfactory.com/CGAL/Members/wiki/Features/Arrangement_on_surface_2 but I cannot access it wants me to login, but I have no login account for this.

I had a quick look at the (master build) files:

  • Arrangement_on_surface_2/group__PkgArrangementOnSurface2Ref.html
  • Arrangement_on_surface_2/index.html

And here I see that on some places \f$ \cal C\f$ is used and on other places: \f$ \mathcal{C}\f$.

A quick overview for \cal:

doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:Given a set \f$ \cal C\f$ of planar curves, the <I>arrangement</I> doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ \cal A(\cal C)\f$ is the subdivision of the plane into zero-dimensional, doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:one-dimensional and two-dimensional cells, called <I>vertices</I>, <I>edges</I> and <I>faces</I>, respectively induced by the curves in \f$ \cal C\f$. doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:The curves in \f$ \cal C\f$ can intersect each other (a single curve may also doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:We construct a collection \f$ \cal C''\f$ of doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:in two steps as follows. First, we decompose each curve in \f$ \cal C\f$ doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:obtaining the collection \f$ \cal C'\f$. Note that an \f$ x\f$-monotone curve cannot doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:be self-intersecting. Then, we decompose each curve in \f$ \cal C'\f$ into doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:curve (or point) in \f$ \cal C'\f$. The collection \f$ \cal C''\f$ may also doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:contain isolated points, if the curves of \f$ \cal C\f$ contain such doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:points. The arrangement induced by the collection \f$ \cal C''\f$ can be doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ \cal A(\cal C) = \cal A(\cal C'')\f$. This graph can be represented using a doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:Given a set \f$ \cal C\f$ of unbounded curves, a simple approach for doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:representing the arrangement induced by \f$ \cal C\f$ would be to clip the doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ \cal C\f$. This process would result in a set \f$ \cal C\f$ of bounded curves doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:(line segments if \f$ \cal C\f$ contains lines and rays), and it would be doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:when one constructs an arrangement induced by a set \f$ \cal C\f$ of arbitrary doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:planar curves, she or he constructs a collection \f$ \cal C''\f$ of \f$ x\f$-monotone doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:subcurves of \f$ \cal C\f$ that are pairwise disjoint in their interior, and these doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:curves representing \f$ \cal C\f$, and by maintaining a cross-mapping between these doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:planar subdivision induced by a set of input curves \f$ \cal C\f$. doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:\f$ C \in \cal C\f$ - or may represent an overlap among several curves doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:in \f$ \cal C\f$. doc/Arrangement_on_surface_2/CGAL/Arrangement_with_history_2.h:representing \f$ \cal C\f$, and by maintaining a cross-mapping between these

and for \mathcal:

doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:An arrangement of intersecting line segments, as constructed in global_insertion.cpp. The segments of \f$ {\mathcal S}_1\f$ are drawn in solid lines and the segments of \f$ {\mathcal S}_2\f$ are drawn in dark dashed lines. Note that the segment \f$ s\f$ (light dashed line) overlaps one of the segments in \f$ {\mathcal S}_1\f$. doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ {\mathcal S}_1\f$ containing five line segments. Then we insert a single doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ {\mathcal S}_2\f$ with five more line segments in an aggregated fashion. doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:Notice that the line segments of \f$ {\mathcal S}_1\f$ are pairwise doc/Arrangement_on_surface_2/Arrangement_on_surface_2.txt:\f$ {\mathcal S}_2\f$ also contain pairwise interior-disjoint segments, doc/Arrangement_on_surface_2/fig_src/ex_10.fig:4 0 0 50 -1 0 18 0.0000 2 270 2055 7262 4562 ${\mathcal S}_2$\001 doc/Arrangement_on_surface_2/fig_src/ex_10.fig:4 0 1 50 -1 0 18 0.0000 2 270 2055 6282 4882 ${\mathcal S}_1$\001 doc/Arrangement_on_surface_2/PackageDescription.txt:Given a set \f$ \mathcal{C}\f$ of planar curves, the <I>arrangement</I> doc/Arrangement_on_surface_2/PackageDescription.txt:\f$ {\mathcal A}({\mathcal C})\f$ is the subdivision of the plane induced doc/Arrangement_on_surface_2/PackageDescription.txt:by the curves in \f$ \mathcal{C}\f$ into maximally connected cells. The cells

So I think also here it would not hurt to make it consistent (and maybe through a macro).

On your questions:

  • what information are you missing?
  • The S in the 2 images of the issue are different.

— You are receiving this because you commented. Reply to this email directly, view it on GitHub https://github.com/CGAL/cgal/issues/5716#issuecomment-841800090, or unsubscribe https://github.com/notifications/unsubscribe-auth/ABVBNOEIPN6A3JFRPXF4XC3TN6PFRANCNFSM446XSVVA .

efifogel avatar May 16 '21 11:05 efifogel

Is this issue solved? In the mentioned page for the overnight build: https://cgal.geometryfactory.com/CGAL/Manual_doxygen_test/CGAL-5.5-Ic-71/master/Snap_rounding_2/group__PkgSnapRounding2Ref.html I don't see the G anymore but a quick grep over Arrangement_on_surface_2 I still see both \cal and \mathcal.

albert-github avatar Apr 27 '22 09:04 albert-github

Just checked against the current master (bf027d4) and I still see \cal and \mathcal not only in Arrangement_on_surface_2but also with other packages. Any progress?

albert-github avatar Sep 07 '23 11:09 albert-github