Geometry_Engine: CollapseToPolyline issues

[IsakNaslundBh]

Two issues found for the CollapseToPolyline method regarding the maxSegmentCount:

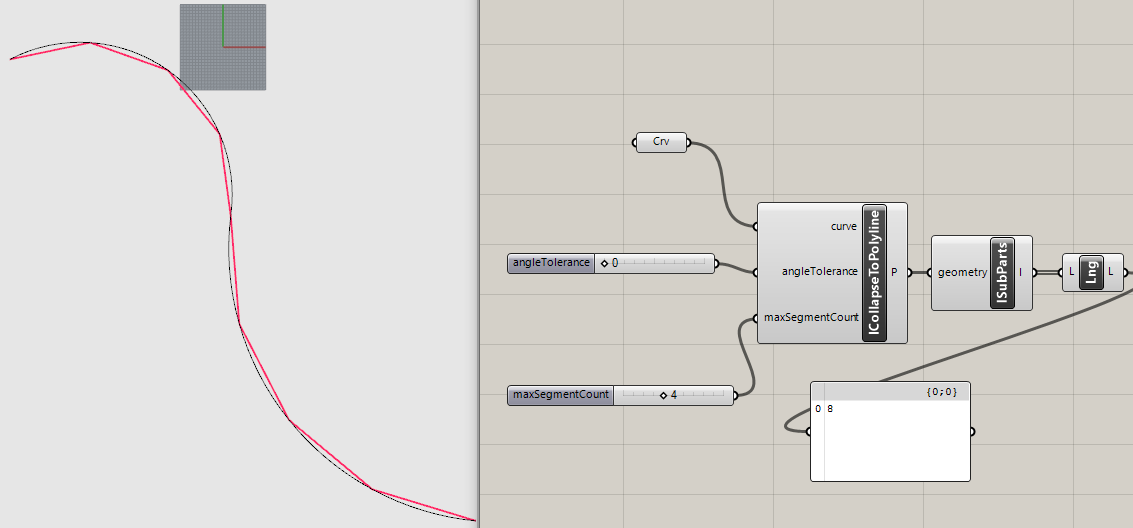
1. The method uses the maxSegmentCount for each subcurve of a polycurve, not enveloped for the curve as a whole, resulting in maxSegmentCount * nbCurvesInPolycurve number of segements. See example bellow where a polycurve made up of two curves is used:

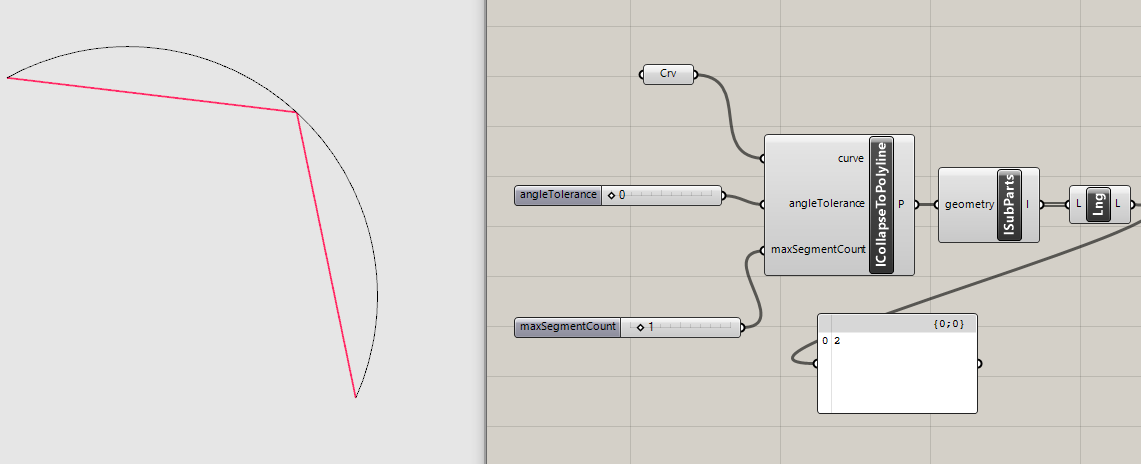
2. For arcs, the method always returns at least 2 segments, even if maxSegementCount is set to 1. Think that if(maxSegementCount <2) we should just return one segement between the start and endpoints:

[pawelbaran]

@LMarkowski adding you, feel free to action once you got a bit of time.

[LMarkowski]

So here is what @IsakNaslundBh and I came up with:

1. It is hard to maintain the required amount of segments, while we do not change shape of lines that were in the polycurve. We could change that and get equally divided points (samplePoints) on the whole curve and join them as polyline. But as we see it works quite fine on arcs-only polycurves, but gets messy when it comes to more complicated figures.

Next option is to left lines as they were and give each arc the "leftovers" after discounting for any lines. Polycurve with 3 lines and 2 arcs maxSegements = 7 7 - lines.Count = 4 4/arcs.Count = 2 2 segments per arc Eventually then divide segments between arcs by the size of an arc.

Last option is to left it as it is and just change the description of input. Not the maxSegments but maxSegments per line or smth.

2. Actually it is not a bug - it's a feature 😉 The number of returned lines depends on angle of an arc: <90 - one line 90 to 180 - two lines 180 to 270 - three lines 270 to 360 - four lines But still, we don't know what to do with it according to the point 1.

What do you guys think?

@epignatelli, I'm adding you to the discussion as I heard that you do a lot around the geometry engine 😉

[epignatelli]

Didn't know to have that bad reputation ahahahah How are you getting the points on the nurbs on the right?

Given a max amount of segments M, and a number of vertices v, we should calculate M - v points. We might then get the length of each curve and distribute the number of points based on the length of the curve. A curve of 1k gets more points than a curve of 10. The points on the curve are just calculated by dividing the curve in m[i] equal segments.

Would something like this work?

[LMarkowski]

It is same method for both polycurves. I just divide whole polycurve into provided number of equal segments and join them as polyline. It gives quite good approximation on slight curves like on the right, but can loose vertices in sharp shapes (like on the left).

Your idea is similiar to what I proposed in second (this starting with "next option") paragraph? I think it is a good course to follow.

I think the point is to decide if it's a good idea to not do anything with parts of polycurves which are already lines. And collapse only arcs. It seems to be efficient but is it what user would expect from this method? Then what if polycurve contains only lines and the maxSegment is less than number of lines? Cut one of? I don't know. Maybe I'm overthinking it 😛

[pawelbaran]

If someone was meant to pick this one up, please note that CollapseToPolyline should be moved to Compute as the input type does not match the output (issue #504).

[kThorsager]

Given a max amount of segments M, and a number of vertices v, we should calculate M - v points. We might then get the length of each curve and distribute the number of points based on the length of the curve. A curve of 1k gets more points than a curve of 10. The points on the curve are just calculated by dividing the curve in m[i] equal segments.

Would something like this work?

Think that sounds good, and is what is happening in DistributeDivisions from #1682 , So if we make it public and move it to Geometry this should be solved with ease.