Use symmetry of copying in crossing minimization in `to_hom_expr`

[nathanielvirgo]

I'm using the following code to generate a TikZ diagram:

using Catlab, Catlab.Theories
using Catlab.Programs
using Catlab.WiringDiagrams
using Catlab.Graphics
import TikzPictures, Convex, SCS

@present P(FreeSymmetricMonoidalCategory) begin
  (M,S,H)::Ob
  psi::Hom(M,H)
  kappa::Hom(H,otimes(H,S))
  u::Hom(otimes(S,M), M)
end

# hack to make the greek letters render correctly
P[:psi].args[1] = Symbol("\\psi")
P[:kappa].args[1] = Symbol("\\kappa")

diagram = @program P (m1::M) begin
    h1 = psi(m1)
    h2, s = kappa(h1)
    m2 = u(s, m1)
    h3 = psi(m2)
  return h3, m2
end

tikz_diag = to_tikz(
    to_hom_expr(FreeCartesianCategory,diagram),
    labels=true,
)

The diagram comes out looking like this:

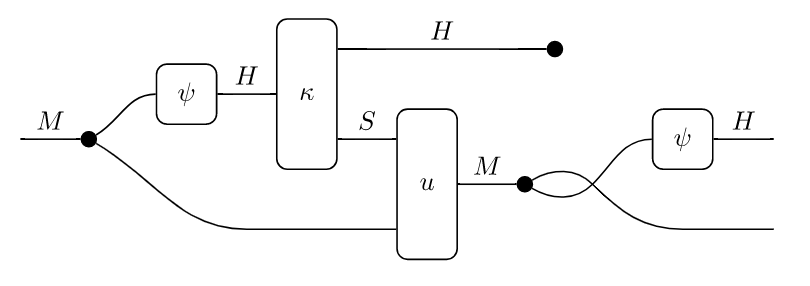
Why is that swap there after the second copy morphism, and is there a way to remove it? (Or better still, have it removed automatically.)

[epatters]

It's because the layout preserves the order of the outer ports (which is meaningful).

If you replace return h3, m2 with return m2, h3, you'll get the desired result.

[nathanielvirgo]

Hmm, but that's not really the desired result - I want the codomain to be H⊗M rather than M⊗H. That gives the result

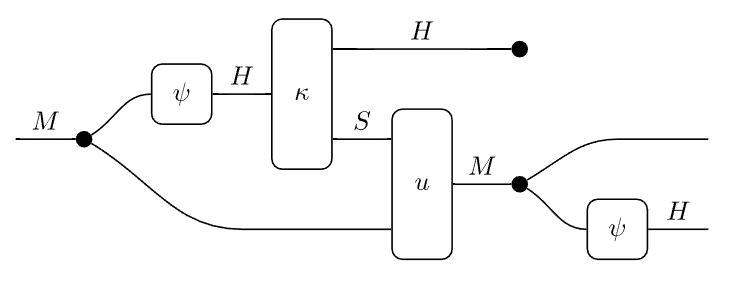
but what I want is this:

[epatters]

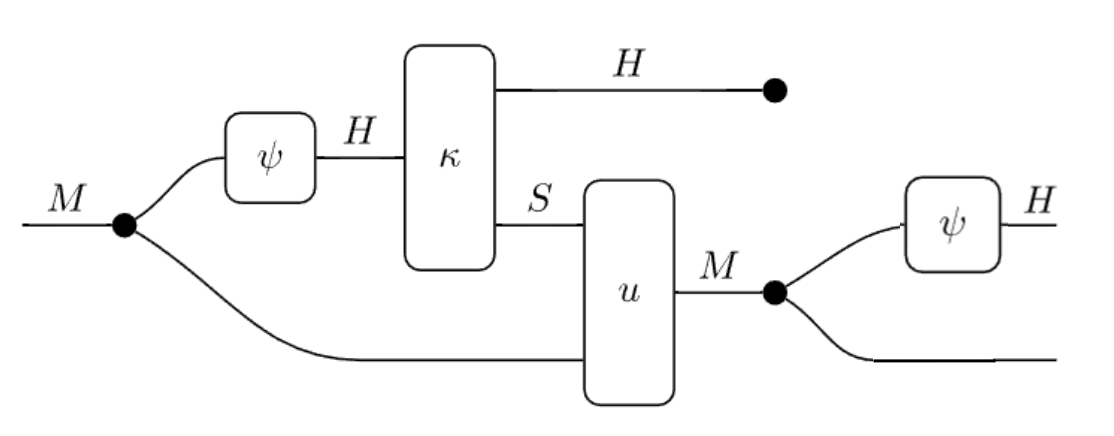
OK, I see what you mean. The problem is that the crossing minimization in to_hom_expr doesn't account for the fact that comultiplication (copying) is commutative:

compose(mcopy(X), braid(X,X)) == mcopy(X)

It won't be entirely trivial to fix this and I'm quite busy right now.

The simplest workaround, if you just need a one-off graphic, is to manually create the morphism expression, using the primitive operations in a cartesian category (compose, mcopy, delete, etc), rather than using @program and then to_hom_expr. That's a bit more work but it isn't too bad.