polygon is sometimes broken

[sjl]

Sometimes the polygon function seems to break and spew lots of strange output.

If you clone down http://github.com/sjl/coding-math and check out commit 3d6ba7a35004215b185674032cbba9b2d4a2e452 you can see an example. Run with:

(ql:quickload 'coding-math)
(in-package #:coding-math.2d.demo)
(defparameter *demo* (make-instance 'cm))

I'm drawing a couple of stars onto the screen. Each star has a list of points, which I draw the circles at. I also draw lines between the points:

(defun draw-star (star)
  (draw-particle (getf star :center))
  ; (draw-polygon (getf star :points))
  (iterate
    (with points = (getf star :points))
    (for (p1 . p2) :pairs-of-list points)
    (draw-circle p1 3)
    (draw-line p1 p2)))

If you uncomment the draw-polygon call there it should fail with something like this:

[sjl]

More polygon weirdness: if I run the following code,

(polygon 0.0 16.65
         -50.0 -8.35
         0.0 -33.35
         50.0 -8.35)

I should get a simple rhombus (because I only passed in four coordinates), but somehow I get a five-sided polygon! If I tweak those numbers sometimes I get what I expect and sometimes I get the weird extra bit, so I think something must be wonky with the triangulation.

[vydd]

Hey, so, I'm back to working on Sketch.

This problem is probably coming from cl-geometry. When I approached the original author with a somewhat similar report we ended up with transferring the maintenance to me, because they had no interest in doing any more active development. I haven't had much time to look at it properly and fix the bugs, though.

Some of the weirdness you might encounter could also be related to the way lines (strokes) are being drawn - line joins, more specifically. Miter is the default and the only join currently available, and the problem with miter is that for very small angles (that some of the triangles created by triangulation might have) endpoints end up being too far away. The proper way to tackle this would be to have a cut off where miter changes into bevel.

I'd like to have more people help me make cl-geometry THE best choice for geometry in CL, so you're more than welcome to join the project (and I'm writing this here as a public call). We can chat about it on #lispgames.

As for the second problem, that's something I'd like to fix in next two weeks. I'll also try preparing a basic roadmap and a set of milestones, so that people can have a better idea about what's on my internal todo list and where Sketch is going.

Thanks

[vydd]

Funny how "back to working on Sketch" actually meant "I'm on a ten month break". Sorry :)

[sjl]

It's fine, I've had a thesis to focus on :)

[Kevinpgalligan]

I may have rediscovered this bug. Documenting my debugging process here.

I'm drawing a mountain scene where the mountain height is varying in time, to give the impression of movement. Mostly the mountain gets drawn correctly via the POLYGON function, but sometimes there ends up being paint outside the polygon.

Here's the happy case. The red dots are the points that mark the edge of the polygon. There are points in the bottom right and bottom left corners so that the mountain goes to the bottom of the screen.

Here's the buggy case. Clearly it's colouring outside the lines.

Here are the x & y coordinates associated with the happy case, I just pass them to POLYGON:

(0 417.6874057601965d0 20 429.90173624550096d0 40 436.66725241007214d0 60 431.5054943514898d0 80 411.53018674336744d0 100 385.0467927999306d0 120 360.7326617349798d0 140 347.2650675065988d0 160 349.15439981002646d0 180 358.4114987507147d0 200 370.6846289206152d0 220 381.95246024113356d0 240 388.193710633887d0 260 386.22744696926566d0 280 377.9696671791911d0 300 367.0214507385711d0 320 356.97000517529347d0 340 351.40251070496794d0 360 352.62843721334133d0 380 358.07371249911984d0 400 365.29310034815535d0 420 371.9211435148715d0 440 375.59241581570245d0 460 374.94465626013084d0 480 371.9383246717213d0 500 367.9525143413313d0 520 364.29318144220247d0 540 362.2662773961404d0 560 365.93221976016264d0 580 379.6275664545465d0 600 397.7848402934933d0 600 500 0 500)

And here they are for the buggy case:

(0 412.6729730407338d0 20 416.0359762879553d0 40 413.4338953818984d0 60 392.59473615330216d0 80 361.1162002874776d0 100 329.6376644216531d0 120 308.79941694437406d0 140 305.77897854671374d0 160 306.3396401446708d0 180 307.18654608649047d0 200 308.03345202831014d0 220 308.59408914564114d0 240 309.55914464615205d0 260 315.4794234687506d0 280 324.42228505728843d0 300 333.36514664582626d0 320 339.2851666788839d0 340 340.719435971895d0 360 344.4296615582641d0 380 350.03413334259403d0 400 355.63860512692395d0 420 359.3486687245161d0 440 360.8197349031721d0 460 366.98778159037965d0 480 376.3049087037839d0 500 385.6220358171881d0 520 391.78981316852196d0 540 391.49419299873205d0 560 383.33900936892644d0 580 371.02021909136465d0 600 358.7014288138029d0 600 500 0 500)

Next step is to dig into the sketch and cl-geometry code that is involved here.

[Kevinpgalligan]

Interesting findings. polygon calls two functions: (1) make-polygon, which generates a list of triangles (which should be coloured in) from the coordinates of the polygon and also returns a list of points defining the edge of the polygon, and (2) draw-shape, which I assume does the dumb tasks of drawing the boundary of the shape and colouring in the triangles.

When I try to reproduce the bug with the following code, where *cs* is the list of coordinates I included in my previous message...

(defsketch debugsnow
          ((width 600)
           (height 500))
        (background +black+)
        (with-pen (make-pen :fill +red+ :stroke +white+ :weight 1)
          (apply #'polygon *cs*)))

...then I get the following result.

The problem seems to lie in how the borders of the shape are drawn, not the calculation of the fill triangles. The jankiness goes away almost entirely when I increase the pen weight to 7.

All of this points to the problem being in draw-shape rather than make-polygon. I see that draw-shape turns the border region into a strip of triangles and then colours in those triangles. It creates the triangle strip using grow-polygon, which I suspect is the source of the problem, although I'm not 100% sure. It also looks to be a different problem to the one encountered by sjl. To be continued.

[Kevinpgalligan]

I belatedly realised that I am an idiot and that I can avoid this problem by not configuring the pen to include a stroke, but for future reference here's the debugging I did. As far as I can tell, the key code is here in draw-shape: https://github.com/vydd/sketch/blob/aea3f9509182749fa80bcc993dc0f284559b2392/src/drawing.lisp#L67-L74

draw-shape takes a list of points that define the border of the polygon (see: red dots below), then creates a set of points that are offset from the border (see: the blue dots below), then interleaves these two lists of points and passes them to push-vertices with the :triangle-strip option. Beyond that I'm not sure where it might be going wrong. There seem to be some unaligned blue & red dots, but they're not near the trouble area.

Here's the code I used to create the above visualisation:

(defsketch debugsnow
          ((width 700)
           (height 600))
        (background +black+)
        ;; Shift all points away from the edge so they're visible.
        (let ((shifted-coords (apply #'append
                                     (mapcar (lambda (xy) (list (+ 50 (car xy))
                                                                (- (cadr xy) 50)))
                                             (sketch::group *coords*)))))
          (with-pen (make-pen :fill +red+)
            (loop for (x y) in (sketch::group shifted-coords)
                  do (circle x y 2.5)))
          (let ((grown (sketch::grow-polygon (sketch::group shifted-coords) 10)))
            (with-pen (make-pen :fill +blue+)
              (loop for (x y) in grown
                    do (circle x y 2.5))))))

Actually, I found that by shifting the shape away from the boundary of the screen, the main jank goes away. So maybe it's related to how the triangle strip interacts with the edge of the screen:

[Kevinpgalligan]

I've now been bitten by the same bug that was first reported by sjl ('The value NIL is not of the expected type NUMBER'). I was able to reproduce it in his coding math demo after running it a few times (the stars are in a random position, so they don't always trigger the bug).

x & y coordinates of points when it works:

((210.84743 385.94913) (209.27464 366.028) (191.97247 356.03003)
 (210.43257 348.37827) (214.59453 328.83337) (227.5763 344.02545)
 (247.45071 341.944) (237.01376 358.985) (245.13484 377.2435)
 (225.70271 372.5833))

When it doesn't work:

((107.51572 290.37234) (104.83386 326.2254) (132.84834 348.76028)
 (97.92133 357.28888) (85.1463 390.8959) (66.24211 360.3138)
 (30.332241 358.54913) (53.575836 331.1198) (44.157383 296.42218)
 (77.42688 310.05206))

And here's a picture of the happy (blue) and sad (red) cases, I can't see an obvious difference between them:

(defsketch bug
          ((width 500)
           (height 500))
        (background +white+)
        (let ((happy '((210.84743 385.94913) (209.27464 366.028) (191.97247 356.03003)
 (210.43257 348.37827) (214.59453 328.83337) (227.5763 344.02545)
 (247.45071 341.944) (237.01376 358.985) (245.13484 377.2435)
                       (225.70271 372.5833)))
              (sad ' ((107.51572 290.37234) (104.83386 326.2254) (132.84834 348.76028)
 (97.92133 357.28888) (85.1463 390.8959) (66.24211 360.3138)
 (30.332241 358.54913) (53.575836 331.1198) (44.157383 296.42218)
                      (77.42688 310.05206))))
          (with-pen (make-pen :fill +blue+)
            (loop for (x y) in happy
                  do (circle x y 3)))
          (with-pen (make-pen :fill +red+)
            (loop for (x y) in sad
                  do (circle x y 3))))
        )

I don't know anything about computational geometry, but I'll try to read up on it and figure out where the code is going wrong. From the stack trace, this is the part of cl-geometry that's causing the problem: https://github.com/vydd/cl-geometry/blob/master/bentley-ottmann.lisp#L120-L130

My understanding is that the algorithm is progressively deleting edges from a tree data structure as it uses them to form new trapezoids. In the error case, it tries to delete an edge that has already been removed from the tree. Not sure yet why that's happening.

[Kevinpgalligan]

Here's a short snippet of code to reproduce the error:

(defsketch bug
          ((width 500)
           (height 500))
        (background +white+)
        (let ((sad ' ((107.51572 290.37234) (104.83386 326.2254) (132.84834 348.76028)
                      (97.92133 357.28888) (85.1463 390.8959) (66.24211 360.3138)
                      (30.332241 358.54913) (53.575836 331.1198) (44.157383 296.42218)
                      (77.42688 310.05206))))
          (with-pen (make-pen :fill +red+)
            (apply #'polygon
                   (loop for (x y) in sad
                         collect x
                         collect y)))))

And a shortened version of the stack trace:

0: (2D-GEOMETRY::DELETE-EDGE #<2D-GEOMETRY:LINE-SEGMENT (30.332241,358.54913)->(53.575836,331.1198)> #<2D-GEOMETRY::SWEEP-LINE 44.157383,296.42218>)
1: (2D-GEOMETRY::RECURSE-BENTLEY-OTTMANN (#(#<2D-GEOMETRY::EVENT-ENDPOINT 66.24211,360.3138> #<2D-GEOMETRY::EVENT-ENDPOINT 77.42688,310.05206> #<2D-GEOMETRY::EVENT-ENDPOINT 66.24211,360.3138> #<2D-GEOMET..
2: (2D-GEOMETRY::TRAPEZOIDIZE-EDGES (#<2D-GEOMETRY:LINE-SEGMENT (107.51572,290.37234)->(104.83386,326.2254)> #<2D-GEOMETRY:LINE-SEGMENT (104.83386,326.2254)->(132.84834,348.76028)> #<2D-GEOMETRY:LINE-SEG..
3: (2D-GEOMETRY:DECOMPOSE-COMPLEX-POLYGON-TRIANGLES #<2D-GEOMETRY:POLYGON [10] {1004449793}> :IN-TEST 2D-GEOMETRY:POINT-IN-POLYGON-WINDING-P)
4: (SKETCH::TRIANGULATE (107.51572 290.37234 104.83386 326.2254 132.84834 348.76028 ...))
5: (SKETCH::MAKE-POLYGON 107.51572 290.37234 104.83386 326.2254 132.84834 348.76028 97.92133 357.28888 85.1463 390.8959 66.24211 360.3138 30.332241 358.54913 53.575836 331.1198 44.157383 296.42218 77.426..
6: (SKETCH:POLYGON 107.51572 290.37234 104.83386 326.2254 132.84834 348.76028 97.92133 357.28888 85.1463 390.8959 66.24211 360.3138 30.332241 358.54913 53.575836 331.1198 44.157383 296.42218 77.42688 310..

Digging into the stack trace, it seems that the problem comes about when trapedoize-edges calls bentley-ottmann to get a list of intersections between the edges, which happens here: https://github.com/vydd/cl-geometry/blob/master/trapezoidation.lisp#L29

So, I will have to do some reading on the Bentley-Ottmann algorithm: https://en.wikipedia.org/wiki/Bentley%E2%80%93Ottmann_algorithm

[Kevinpgalligan]

I've been thinking, "why do we need to check for intersections if the edges of the polygon never cross each other?", but self-intersecting polygons are a thing , e.g. https://en.wikipedia.org/wiki/Complex_polygon

A simple fix, if we assume non-intersecting polygons, would be to have a separate version of trapedoize-edges that doesn't bother calling bentley-ottmann because it knows that the edges don't intersect. Or if they do, it's only at their endpoints.

Anyway, I'm reading up on the Bentley-Ottmann algorithm now, let's see if I can figure out what's wrong with the implementation.

[Kevinpgalligan]

Currently in debugging hell. I've numbered the points of the star, the ID of a line segment is then the numbers of its 2 associated points:

The algorithm works by moving a vertical line from left to right. The line stops for 3 types of events: the start (left point) of a line segment, the end, and intersections of line segments. When it hits the left point of a line segment, it adds the line segment to a binary search tree (BST). When it hits the right point, it removes the line segment from the BST. Here's how this plays out with our bug case, I print each event as it happens as well as the edge that is involved in that event and the state of the BST after the event:

Endpoint: LEFT (7 6)
(7 6) 
Endpoint: LEFT (7 8)
(7 8) (7 6) 
Endpoint: LEFT (9 10)
(7 8) (7 6) (9 10) 
Endpoint: LEFT (9 8)
(7 8) (7 6) (9 10) (9 8) 
Endpoint: RIGHT (9 8)
(7 8) (7 6) (9 10) 
Endpoint: RIGHT (7 8)
[error happens here]

So, the edge (7 8) is still in the search tree when we try to remove it, but we fail to find it. I suspect that this is due to a bug in the compare function for the search tree, which is implemented here: https://github.com/vydd/cl-geometry/blob/24eddedc47b931cec27361752736ef0b54fc9984/bentley-ottmann.lisp#L53

It's quite a tangled bit of code, but I think I'm close to identifying the bug.

[sjl]

@Kevinpgalligan I haven't used Sketch in years, so apologies if this is noise, but that comparison function you linked is not transitive:

(defparameter *a* (make-line-segment (make-point -2 4)  (make-point 0 -4)))
(defparameter *b* (make-line-segment (make-point -4 -3) (make-point 0 -4)))
(defparameter *c* (make-line-segment (make-point -5 1)  (make-point -4 0)))
(defparameter *p* (make-point 0 2))

(order-line-segments-at-point *a* *b* *p*) ; => T
(order-line-segments-at-point *b* *c* *p*) ; => T

;; a < b and b < c should imply a < c, but doesn't
(order-line-segments-at-point *a* *c* *p*) ; => NIL

which seems problematic if it's used for sorting, etc.

[Kevinpgalligan]

Yeah, I believe that's where the problem is. The BST is supposed to order the line segments from lowest to highest y value, based on where the vertical sweep line currently is. Clearly, (7 8) should be above (7 6) by the time the vertical sweep reaches the right-most point of (7 8), but it is not ordered that way in the tree. I'm trying to figure out why that is the case.

[sjl]

Assuming trees:make-binary-tree wants a transitive comparison function (which, unless it's something wild, it probably does) then giving it one that's not transitive will probably result in a mangled internal state (like trying to cl:sort with something non-transitive).

In the example I gave above:

The edge case being hit is:

All three lines (when extended from segments) intersect the sweep line at the same point.

Line segments a and b end at the same point, which triggers the

(point-equal-p (right-endpoint lv) (right-endpoint rv));both lines terminate at the same point

clause in the (= y1 y2) case and results in comparing them with reverse slope.

Any other combination of line segments, a and c or b and c, don't have the same endpoint, and so are compared by vanilla slope.

[sjl]

(It's not clear to me why those endpoint comparisons are used in the tie breaker case at all, but I don't know anything about the algorithm itself.)

[Kevinpgalligan]

In your sample code you seem to have accidentally set point *b* to start at y=-3, making it below *c*. Which means that (order-line-segments-at-point *b* *c* *p*) should be NIL, not T (assuming my understanding of the expected behaviour is correct). Also, *a* is above *c*, so (order-line-segments-at-point *a* *c* *p*) should return T. It should also be triggering the reversed slope for those cases. I'm not sure if that's the bit that's causing the star example to fail, though.

[sjl]

Sorry, yeah, the drawing was wrong, the actual edge case looks like:

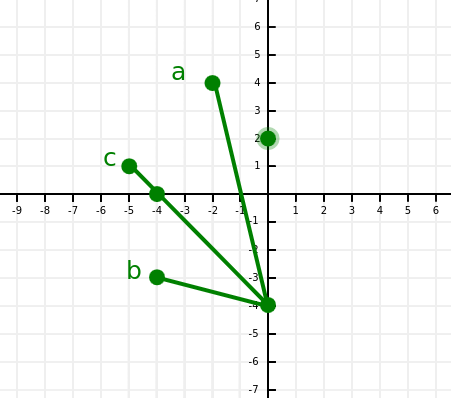
But the example code still demonstrates a non-transitive comparison function:

• a < b = t because it compares reverse slope (because they end in the same point).
• b < c = t because it compares vanilla slope (this seems wrong, but maybe I don't have a good idea of what "above" means for this algorithm).
• a < c = nil because it compares vanilla slope.

which is probably going to mangle the binary tree's state when used as an ordering predicate.

[Kevinpgalligan]

I think I've identified the bug. The BST stores line segments from highest to lowest (in terms of their y position). Or, if two segments have the same start point, it orders them so that the one with higher slope comes first. That's the specification that I've derived from the ordering function, at least.

So it is incorrectly placing (7 8) before (7 6) in the BST when the vertical scan line starts at point 7. (7 6) should be "higher", and hence earlier in the BST order, because it has a higher slope. This is clear if we plot the points of the star with the origin in the bottom left corner this time.

The mis-ordering happens due to numerical precision issues: the ordering function turns the segment (7 8) into a "line" object and evaluates its y coordinate at the starting x position, which gives y=358.54913. And it gives a y coordinate of y=358.5491 (missing a 3 at the end) for (7 6), even though they have the same start point. So it doesn't trigger the special logic for (= y1 y2), which would use the slope, and instead ranks (7 8) "above" (7 6). Then, when the vertical scan line reaches the end point of (7 8), the y values of the segments are evaluated again and (7 8) is considered "below" (7 6), which sends us the wrong direction in the tree. That's what I think is happening, anyway.

I guess this is why the documentation in cl-geometry says "The system assumes exact rational arithmetic, so no floating point coordinates are allowed. This is not checked when creating geometric objects." And there is also a section on the Wikipedia page for Bentley-Ottmann devoted to numerical precision issues: https://en.wikipedia.org/wiki/Bentley%E2%80%93Ottmann_algorithm#Numerical_precision_issues

Possible solutions:

• In cl-geometry, if we fail to find an item in the tree, then remove all the nodes and add them back in, because the tree must be in the wrong order due to numerical precision issues. Or, do a linear O(n) scan through the tree rather than the typical O(logn) binary search. The Bentley-Ottmann algorithm would still give wrong results due to numerical precision issues, but at least it wouldn't fail catastrophically. We would have to implement this in multiple places where the algorithm interacts with the tree, not just the edge deletion.
• In cl-geometry, add a separate interface that trapezoidises non-self-intersecting polygons so that we don't have to call the Bentley-Ottmann algorithm to find the self-intersection points. Then we could specify in the sketch interface that polygons should be non-self-intersecting. Not sure if this would break anyone's use case. Also, this does not guarantee that we would avoid numerical precision issues in other parts of cl-geometry, I'd have to check where else this BST is being used.
• In sketch, convert all coordinates to rationals before passing them to cl-geometry.

Any other ideas or thoughts on what would be the best solution, @vydd? I'm happy to implement any of these ideas, but I don't know which is the right one, hehe.

[Kevinpgalligan]

I've confirmed the bug after stepping through the tree operations in more detail. Here's what the BST looks like at each step. The sweep line goes from left to right. It adds a line segment to the BST when it hits the start point of the line segment, and removes the line segment when it hits the end point. Line segments should be ordered in the BST from highest to lowest based on their y coordinate, and if they start at the same point, they should be ordered so that the one with higher slope comes first. At least, that is how the original author expected the comparison function to work.

Another solution has occurred to me, we could avoid the numerical precision issue by checking: (1) is this the start point of the line segment? (2) If so, then just set its y value to that of the start point, rather than trying to calculate the y value using the line equation. We could still run into the bug if a line segment A intersects the start point of another line segment B, because then they could be evaluated so that A<B when the vertical sweep line is at the start of B (due to numerical precision), but as soon as we move past B they're no longer in the correct order. And I'm not sure how to resolve that. But that seems like a degenerate case. The trick I've described would at least handle the error we're seeing here, I believe. I'll try it out and report back.

The intransitive behaviour pointed out by @sjl may also be a source of bugs -- thanks for your debugging help!

[Kevinpgalligan]

I tried the fix where we avoid the numerical calculation of y in the comparison function, if possible, and it fixed the error case I isolated above. But when I ran slj's demo a bunch of times it still mostly failed, and it also failed on the sketch that I was working on when I originally ran into this bug. I'm not sure that I want to dig into numerical precision crap any further.

I've also tried the fix where we convert all coordinates to rationals before passing them to cl-geometry (which is literally only used in sketch's triangulate function), and it does in fact fix the behaviour! Even my original sketch works. But it seems a lot slower than before. I'm not sure if that's because we're creating a bunch of rationals in every frame, or because of slow rational computations that are happening in cl-geometry, but it's not ideal.

So, my preferred solution is now to change the interface of cl-geometry and allow the caller to specify when polygon edges are non-self-intersecting. Then it can skip the Bentley-Ottmann algorithm and we will hopefully not run into any more numerical precision issues. This would require specifying in the sketch interface that polygons be non-self-intersecting. I will test out this solution and see if it works, then send a pull request and move on with my life, haha.

[Kevinpgalligan]

IT WORKED. And it's as fast as before. Preparing pull requests now.

[Kevinpgalligan]

I spoke too soon. It worked with my sketch, but the star example is still buggy. The problem is that, even though we avoid calling the Bentley-Ottmann algorithm, the "trapezoidize" algorithm uses a similar data structure & approach to divide the polygon into trapezoids, and so it triggers the same numerical precision issues (I think). I'm going to take a break for the weekend, no longer sure what's the best path forward. The Processing programming language seems to call to an OpenGL interface for tessellating polygons (this, I believe). That might be the way to go to avoid edge cases in cl-geometry without switching to rational coordinates.

[Kevinpgalligan]

I got drawn back in and attempted another hacky fix. When we're comparing the y values y1 and y2 of 2 line segments, I added a check for whether either y1 or y2 is a float. If so, and if (< (abs (- y2 y1)) some-small-float), then I converted the offending line segment(s) to rational coordinates and re-computed the y value(s), because there's the possibility of numerical precision mucking things up. This didn't work.

I then went searching and discovered that cl-opengl actually has a wrapper around OpenGL's GLUtesselator interface, see here: https://github.com/3b/cl-opengl/blob/e2d83e0977b7e7ac3f3d348d8ccc7ccd04e74d59/glu/interface.lisp#L35

And here is an example of how it's used: https://github.com/3b/cl-opengl/blob/e2d83e0977b7e7ac3f3d348d8ccc7ccd04e74d59/examples/redbook/tess.lisp

I'm not sure how easily this could be incorporated into sketch. It seems to be used for directly drawing polygons, it doesn't seem to give access to the triangle tessellation that it generates. I will take a shot at adding a new drawing function for polygons that uses the OpenGL tessellator approach.

[Kevinpgalligan]

For the record, here is my partial attempt at incorporating the tess.lisp example that I shared above:

https://github.com/Kevinpgalligan/sketch/commit/fbf67656d044024bea00248501425e5e140c1f23

I'm not sure if I've implemented all the required callbacks. Also, I didn't integrate it with the rest of the OpenGL code. Maybe sketch's vertex buffer must be bound first? Maybe the tessellation interface is from an older version of OpenGL and is incompatible with the part of the API used by sketch?

Anyway, I'll come back to this when I've learned more about OpenGL or when I'm feeling adventurous. Anyone else is feel free to take a shot at it. Until then, the simplest workaround is to use rational coordinates when drawing polygons.

[vydd]

Thank you for the great analysis! I think the way forward is probably to implement triangulation from scratch. I'll try to work on that in the next few days as I have some time, and we'll see.

[Kevinpgalligan]

My sense is that tesselation is difficult to get right with floating point coordinates, and it might make more sense to incorporate OpenGL's ready-made solution if that's at all possible. I don't know if the Tesselator API can be mixed with the parts of OpenGL that Sketch uses, though.

[Kevinpgalligan]

FINALLY 🎉

[vydd]

Thank you all. I didn't understand initially that the tessellator we were talking about was from GLU, and not https://www.khronos.org/opengl/wiki/Tessellation . After 8 years, we've now switched to https://github.com/orthecreedence/glu-tessellate with a simple +6,-8 change.

[Gleefre]

This should probably be mentioned: glu-tesselate uses GLU, which is somewhat deprecated; so it would be nice to switch to another library; preferably written in pure CL.