[Feature Request] Directly access scaled uncertainties using re-calibration model.

[CompRhys]

Having trained a re-calibration model using this library it is not obvious how to actually extract the calibrated uncertainties for the data points. As well as being generally useful it also means that some metrics in the code do not have equivalent support for re-calibration e.g. I currently can not see how I could check how the sharpness of my model is affected by the re-calibration.

Can a function be added for this functionality i.e. rescale_std_from_recal(y_pred, y_std, recal_model).

[CompRhys]

More generally since most methods rely on sampling rather than predicting the moments of a Gaussian distribution it may be helpful to add a calibration based on the empirical distribution rather than the CDF of an assumed Gaussian?

https://github.com/TheClimateCorporation/properscoring implements some ensemble sample methods for the CPRS and Brier score. I believe that that repo is no longer active and so it could make sense to pull some of the code over here (with attribution).

I will look into what would be needed to change the calibration code to use empirical distributions. I.e. if your uncertainty comes from a deep ensemble with say only 10 learners relying on ideas from the CLT to assume that the mean of the learners is Gaussian seems a little optimistic with so few samples.

I also highlight this paper (https://arxiv.org/abs/1905.11659) which suggests that the re-calibration method of [Kuleshov et al., 2018] can be misleading (Figure 1a). Perhaps it would be nice in the longer term to implement multiple calibration models here!

[YoungseogChung]

Thanks for your suggestions, Rhys! We certainly acknowledge the need for the functionality to extract recalibrated uncertainties, and this is a feature we aim to add in very soon.

We chose to focus on the Gaussian parameterization of predictive uncertainty in this initial release. We will expand to other representations in the coming releases, including quantiles and empirical distributions. Thanks for looking into how to potentially incorporate this into the toolbox as well!

We appreciate the reference on recalibration. The recalibration by [Kuleshov et al.] definitely has its limits, as it is only really aimed at average calibration. We will be looking into other recalibration algorithms as well in the coming releases.

In the meantime, please feel free to suggest more references or features!

[CompRhys]

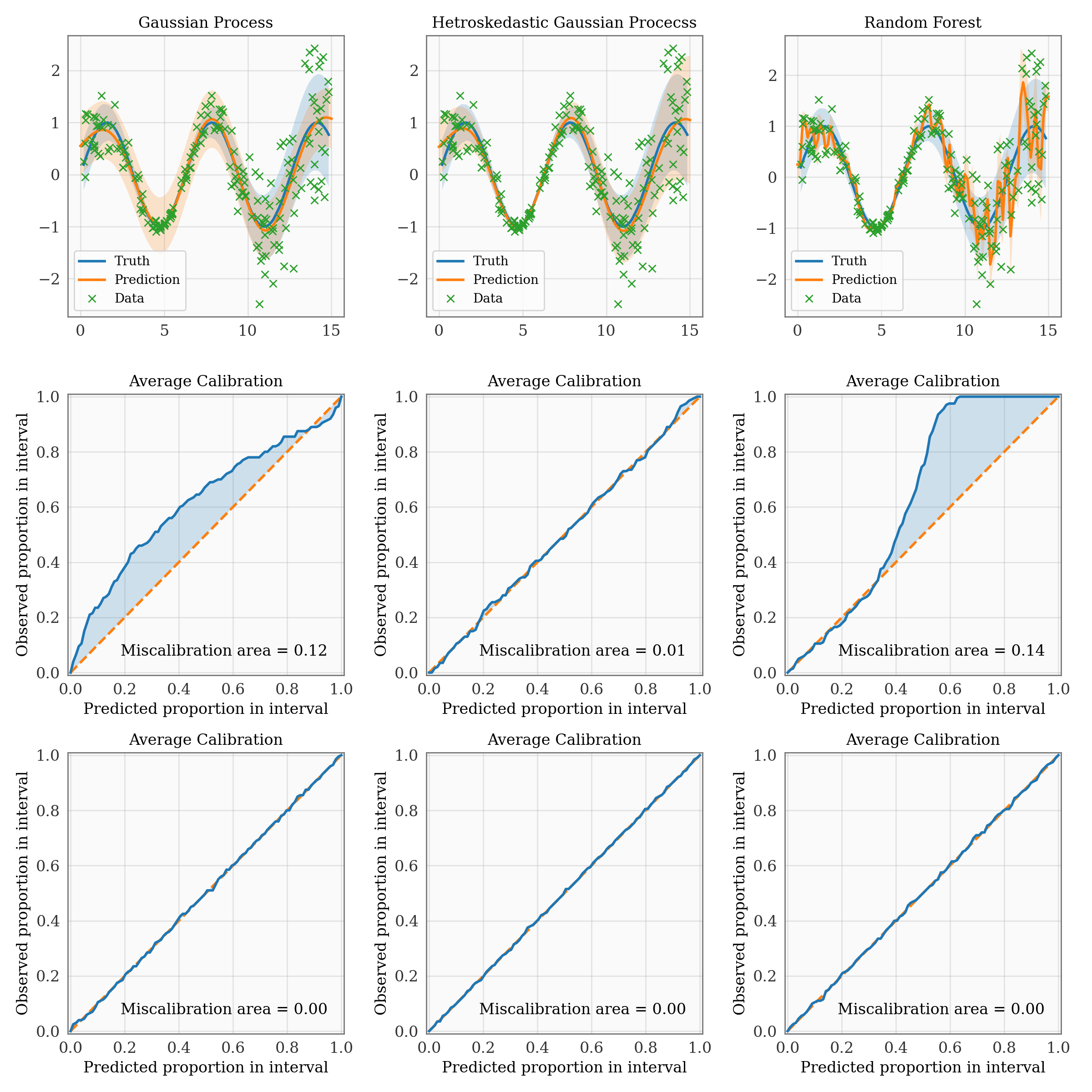
Thanks, I have been looking it it myself and I just can't see how to actually extract the re-calibrated uncertainties for the Kuleshov et al approach as we can only get the standard deviation from the re-calibrated CDF if the random variable is non-negative which isn't the case here as u = (y_lab - mu_pred)/sigma_pred. I am sure I must be missing something but not sure where!?

The re-calibration plots in some ways are too good in the toy example above which gives me cause for doubt - how can a homoskedatic model (i.e. the GP) end up being calibrated to the same level as a hetroskedastic model (hetGP/RF) if all we can do is update say sigma* = f(mu, sigma).

[YoungseogChung]

Sorry about the late response!

On extracting recalibrated uncertainties, we realized it is somewhat difficult with the current recalibration algorithm since the recalibration model maps probabilities to probabilities. For any expected probability p_1 (with sigma_1) and it's corresponding recalibrated probability p_2, we could solve for a "recalibrated sigma", sigma_2, but this sigma_2 would be different for each p_1, so in fact, the current recalibration algorithm doesn't map conditional Gaussians to conditional Gaussians. For a single p_1, solving for sigma_2 would correspond to solving normal_quantile_function(p_2; mu_1, sigma_1) = normal_quantile_function(p_1; mu_1, sigma_2). This is still cumbersome, and we are actively working on trying to devise a more elegant solution to this and will let you know when we have something. We are not sure we follow what you are saying about the non-negative random variable.

On your second point, the key thing to keep in mind is that this is average calibration. When a prediction interval covering x% of the data is requested and x% of the entire dataset falls in that prediction interval, the model is on average calibrated. However, as you have observed here, this is not always a good metric. We suspect that if you look at adversarial group calibration that the heteroskedastic model will do much better here. Adversarial group calibration is also implemented in the toolbox. Lastly, for this calibration example, results are looking especially good since the same dataset was used for training, recalibration, and testing (something that should never be done in practice).

[CompRhys]

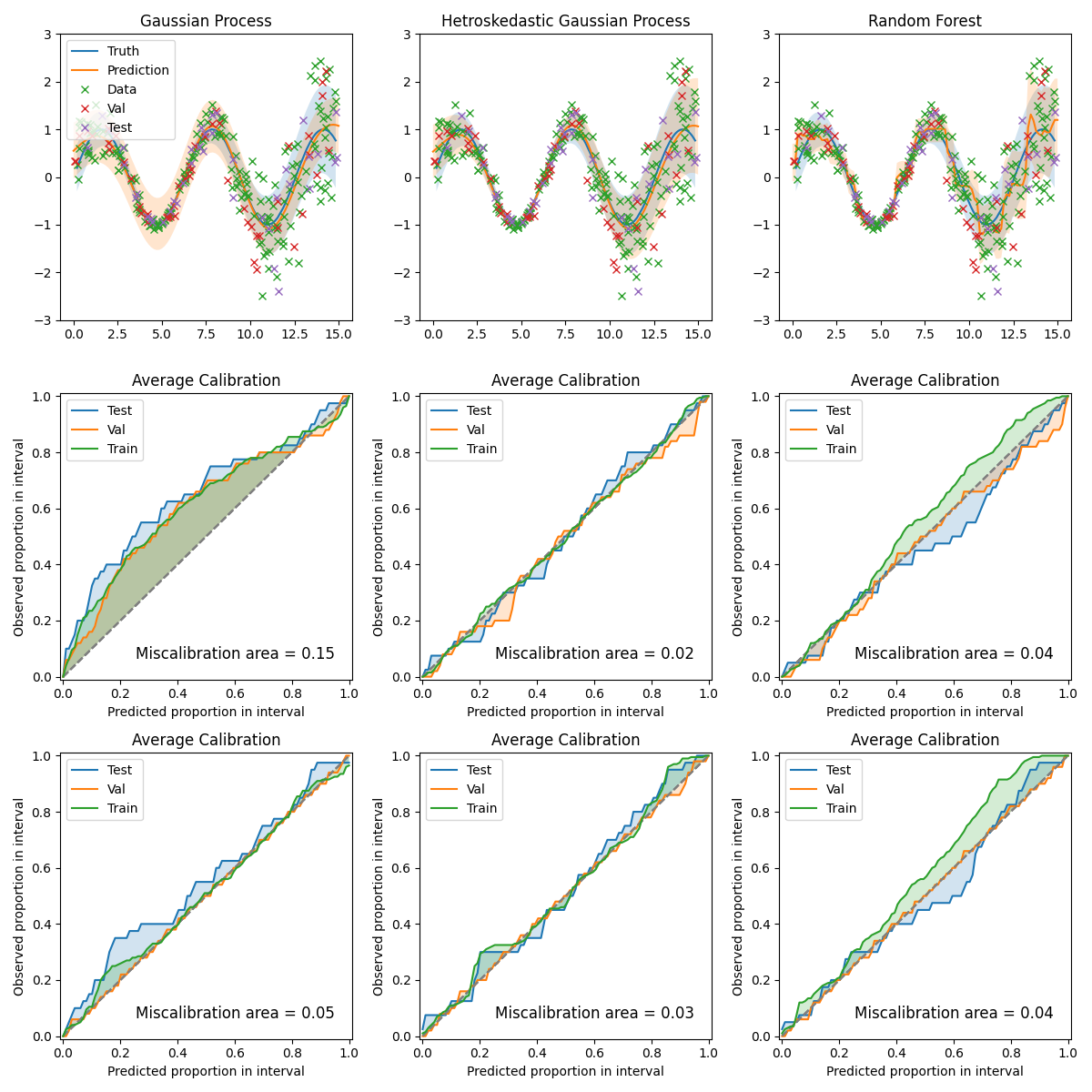
For completeness of this issue here is a revised version of the plot where the miscalibration areas in the calibration plot rows are for a test set and the calibration model is trained on a separate validation set. This plot does indeed look more reasonable! I think the plots in the README and examples might have misled me slightly as they are of the first type rather than the second so I didn't think critically enough about it.

[WardLT]

Is this issue fixed by the addition of the "get_recalibrator" functions? (i.e., get_std_recalibrator)

[CompRhys]

I have just looked around the and I think that function simply identifies a scalar for scaling the uncertainty by to improve calibration based on the chosen metric.

https://github.com/uncertainty-toolbox/uncertainty-toolbox/blob/946433b2bca9eb93b06b144cffdb32faf0a9c64f/uncertainty_toolbox/recalibration.py#L215-L216

I think I was initially interested in this idea that if we use isotonic regression to adjust the quantiles of our distribution of normalised residuals is there some way to get a actually get a number for the uncertainty(/confidence interval) of a single point. I am still confused about whether or not this can actually be done as Kuleshov et al. suggest, I think this is basically what @YoungseogChung was getting at above that the isotonic regression algorithm is somewhat difficult to actually invert to get uncertainty(/confidence interval) of a single point as we don't know the residual in a prospective setting.

[WardLT]

Makes sense. I haven't been able to work out how to take that isotonic regressor and use it to calibrate individual uncertainties either. At least getting a single scaling value is a step in that direction.

[CompRhys]

@YoungseogChung any updates on inverting the uncertainty scaling with isotonic regression?

[YoungseogChung]

Hi @CompRhys,

Sorry for the slow response.

I've been giving this some more thought, and as far as I can tell, I think there are only a couple of ways around this, none of which may be all that satisfactory:

1. Similar to the functionality in get_std_recalibrator, use black-box optimization to find a multiplicative scaling factor which minimizes the miscalibration of the resulting Gaussian distribution with scaled standard deviation. This is just finding a constant to get a "best-fit" Gaussian (according to the miscalibration criterion for the optimization).

2. Draw samples according to the quantile mapping learned by the isotonic regression. This functionality is not in this toolbox yet, but has been implemented in others, e.g. in this repo. The steps are as follows:
   1. Assume a predictive distribution f. We can assume this is Gaussian.
   2. Draw N samples from the Unif(0, 1)....i.e. the uniform distribution between 0 and 1, denote this set as S. S is a set of quantile levels we would query from the predictive distribution.
   3. Input S into the isotonic regression recalibration model to get a set of recalibrated quantile levels, which we denote as R.
   4. Find the quantiles from f which correspond to the quantile levels in R, and denote this set of recalibrated quantiles as T.

The output set of points, T, is essentially a set of samples from the recalibrated distribution. Following the above steps, we find that this set T of samples from the recalibrated distribution can be highly non-Gaussian, even if the original distribution f is Gaussian. So I really do not think there is a clean and concise way of accessing the recalibrated uncertainties, since the distribution implied by the recalibration is highly complex.

Hope this helps, and let me know if this makes sense to you.