FEA add newton-lsmr solver to LogisticRegression and GLMs

[lorentzenchr]

Reference Issues/PRs

Supersedes #23507. Fixes #16634.

What does this implement/fix? Explain your changes.

This PR adds a further NewtonSolver: NewtonLSMRSolver. This solver uses the iteratively reweighted least squares (IRLS) formulation of a Newton step. This means the inner solver uses the square root of the Hessian and solves the corresponding least squares problem (as opposed to solving the normal equation as "newton-cholesky" is doing) with the iterative LSMR solver.

This solver is therefore suited for dense and sparse X.

Any other comments?

The multinomial/multiclass case deserves special attention as there are different ways to look at the Hessian $X' W X$:

• Naive: Use, e.g. for n_classes=3

  X = [X 0 0]  W = [W00 W10 W00]  y = [y==0    0    0]  coef = [coef_class_0]  ...
      [0 X 0]      [W10 W11 W00]      [   0 y==1    0]         [coef_class_1]
      [0 0 X]      [W20 W10 W22]      [   0    0 y==2]         [coef_class_2]
  

• Consider every 1d-array/2d-array as a 2d-/3d-array with its 2nd/3rd dimension having all n_samples. Then $W = \mathrm{diag}(p) - p'p$ and $p$ the probability array in n_classes (and n_samples as "depth"). Now, one can use the LDL decomposition of this particular matrix $W$, analytically given in https://doi.org/10.1111/j.2517-6161.1992.tb01875.x, use $\sqrt{D} L'$ as square root of $W$. This is the chosen approach.

[lorentzenchr]

@ogrisel @mathurinm @TomDLT @agramfort @rth might be interested as this seems to be new ground for GLM solvers, especially the multinomial logistic regression!

It was a very stony path to arrive with all (added) tests green. Right now, I've no energy to do extensive benchmarking. But I hope, that this work will become useful and find its way into scikit-learn, in the end. I'm sure, there are opportunities left for performance optimization.

[ogrisel]

Glad to see this! I just re-ran the previous benchmark for Poisson regression on the French MTPL dataset from the previous PR:

• https://github.com/scikit-learn/scikit-learn/pull/23507#issuecomment-1144003707

and here are the results on my laptop:

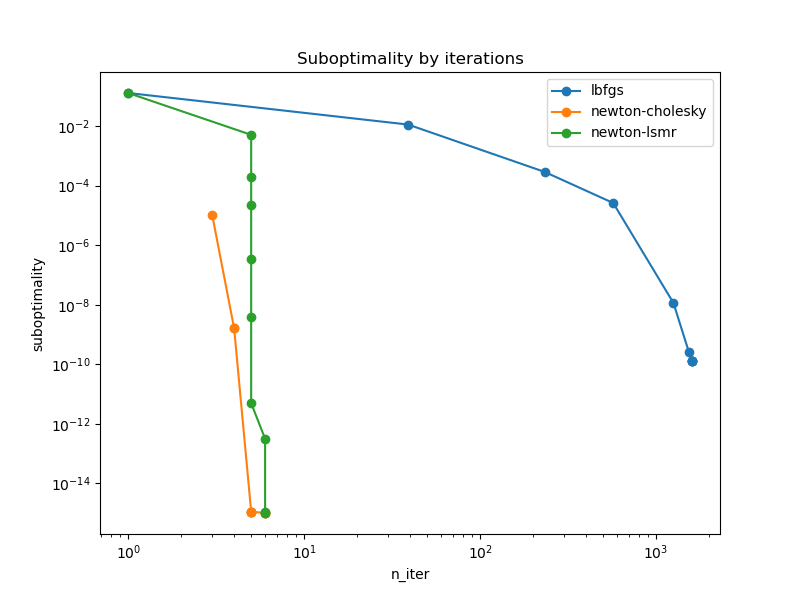
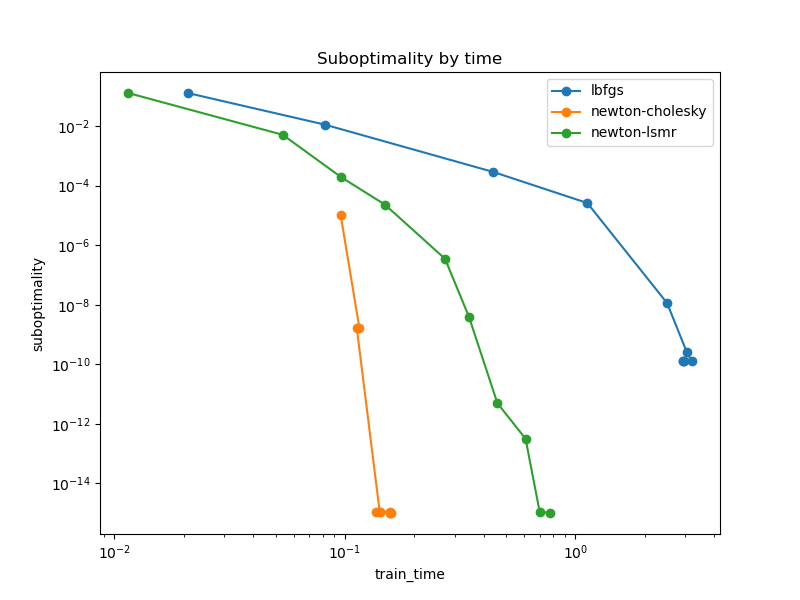
so this looks very good.

[ogrisel]

I have adapted the above benchmark to turn it into an imbalanced multiclass classification problem by binning the target. Since 0 is overly represented, when choosing a large number of bins and the quantile strategy, many bins are collapsed to 0.

Here is the code:

import warnings
from pathlib import Path
import numpy as np
from sklearn.compose import ColumnTransformer
from sklearn.datasets import fetch_openml
from sklearn.linear_model import PoissonRegressor, LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model._linear_loss import LinearModelLoss
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
from time import perf_counter
import pandas as pd
import joblib


m = joblib.Memory(location=".", verbose=0)


@m.cache
def prepare_data():
    df = fetch_openml(data_id=41214, as_frame=True, parser='auto').frame
    df["Frequency"] = df["ClaimNb"] / df["Exposure"]
    log_scale_transformer = make_pipeline(
        FunctionTransformer(np.log, validate=False), StandardScaler()
    )
    linear_model_preprocessor = ColumnTransformer(
        [
            ("passthrough_numeric", "passthrough", ["BonusMalus"]),
            (
                "binned_numeric",
                KBinsDiscretizer(n_bins=10, subsample=None),
                ["VehAge", "DrivAge"],
            ),
            ("log_scaled_numeric", log_scale_transformer, ["Density"]),
            (
                "onehot_categorical",
                OneHotEncoder(),
                ["VehBrand", "VehPower", "VehGas", "Region", "Area"],
            ),
        ],
        remainder="drop",
    )
    y = df["Frequency"]
    w = df["Exposure"]
    X = linear_model_preprocessor.fit_transform(df)
    return X, y, w


X, y_orig, w = prepare_data()

print("binning the target...")
binner = KBinsDiscretizer(
    n_bins=300, encode="ordinal", strategy="quantile", subsample=int(2e5), random_state=0
)
y = binner.fit_transform(y_orig.to_numpy().reshape(-1, 1)).ravel().astype(np.int32)

# X = X.toarray()
X_train, X_test, y_train, y_test, w_train, w_test = train_test_split(
    X, y, w, train_size=10_000, test_size=10_000, random_state=0
)
print(f"{X_train.shape = }")
print("y_train.value_counts() :")
print(pd.Series(y_train).value_counts())

results = []
slow_solvers = set()
for tol in np.logspace(-1, -10, 10):
    for solver in ["lbfgs", "newton-cg", "newton-lsmr"]:
        if solver in slow_solvers:
            # skip slow solvers to keep the benchmark runtime reasonable
            continue
        tic = perf_counter()
        # with warnings.catch_warnings():
        #     warnings.filterwarnings("ignore", category=ConvergenceWarning)
        clf = LogisticRegression(
            C=1e12, solver=solver, tol=tol, max_iter=10000
        ).fit(X_train, y_train)
        toc = perf_counter()
        train_time = toc - tic
        if train_time > 200:
            # skip this solver from now on...
            slow_solvers.add(solver)
        # TODO: handle the regularization term...
        train_loss = log_loss(y_train, clf.predict_proba(X_train))
        n_iter = clf.n_iter_[0]
        result = {
            "solver": solver,
            "tol": tol,
            "train_loss": train_loss,
            "train_time": train_time,
            "train_score": clf.score(X_train, y_train),
            "test_score": clf.score(X_test, y_test),
            "n_iter": n_iter,
            "converged": n_iter < clf.max_iter,
        }
        print(result)
        results.append(result)


results = pd.DataFrame.from_records(results)
filepath = Path().resolve() / "bench_multinomial_logistic_regression_mtpl.csv"
results.to_csv(filepath)


import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt


results = pd.read_csv(filepath)
results["suboptimality"] = results["train_loss"] - results["train_loss"].min() + 1e-15
fig, ax = plt.subplots(figsize=(8, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="n_iter", y="suboptimality", loglog=True, marker="o", label=label, ax=ax
    )
ax.set_ylabel("suboptimality")
ax.set_title("Suboptimality by iterations")

fig, ax = plt.subplots(figsize=(8, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="train_time", y="suboptimality", loglog=True, marker="o", label=label, ax=ax
    )
ax.set_ylabel("suboptimality")
ax.set_title("Suboptimality by time")
plt.show()

DISCLAIMER: the plot above displays the unpenalized train_loss while the model where fitted with C=1e12 so take those results with a grain of salt. I should have tried to completely disable penalization. And maybe also plot the (unpenalized) test negative log likelihood.

EDIT: I did another run with C=np.inf and the results are similar:

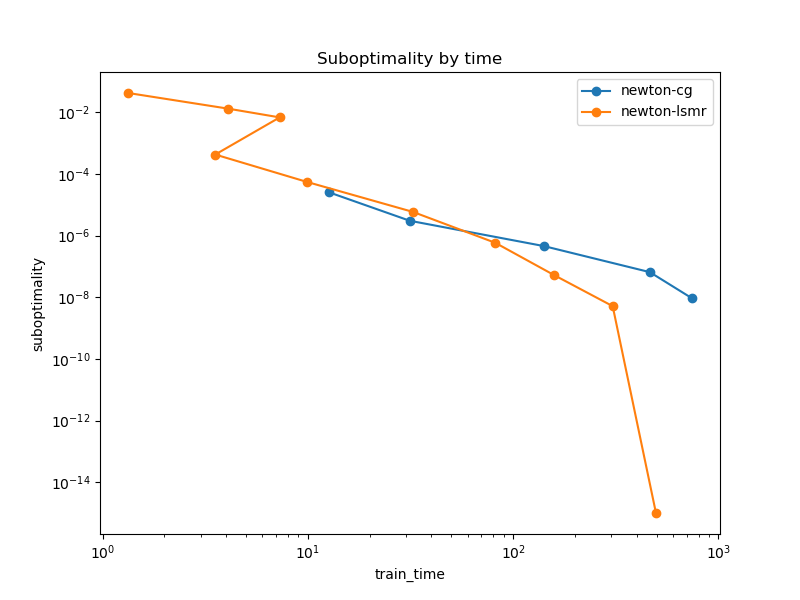
This task is very challenging for all solvers and I had to decrease the number of samples to get it run in a reasonable time on my laptop. I also stopped recording solver when tol decreases to the point where a single fit would last more than a few minutes.

Here are the resulting plots:

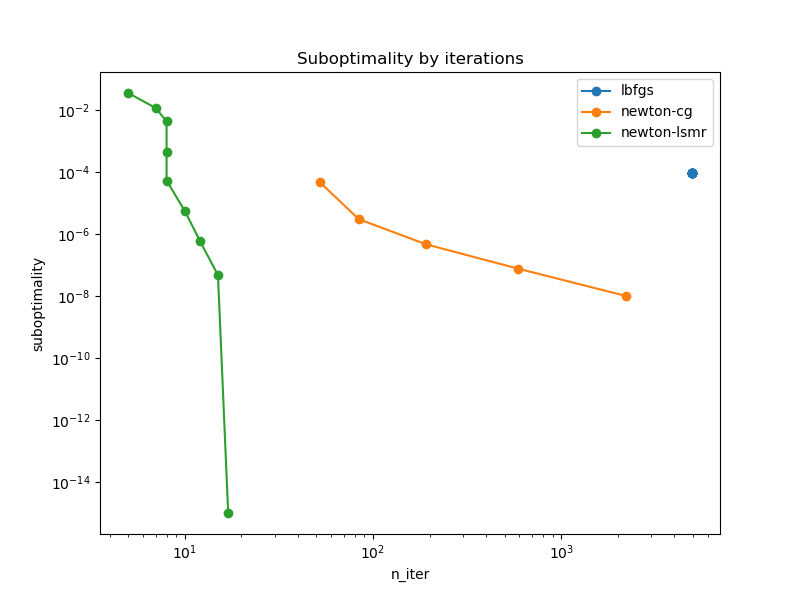
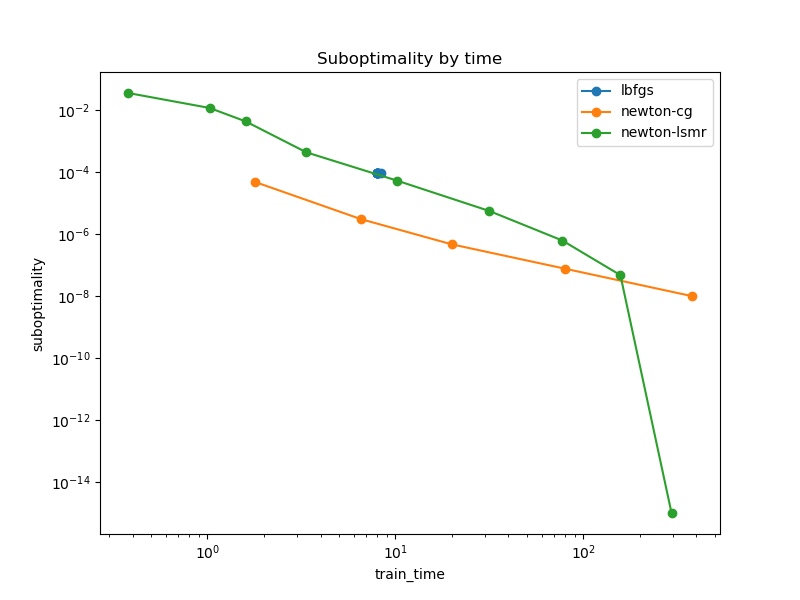
Note that the handling of the stopping criterion of LBFGS is not working properly for the LogitistRegression estimator as was previously reported in #24752.

newton-lsmr is slower than alternatives at the beginning but can still converge to low tol values while newton-cg would probably a lot more time (if it ever could in the first place).

Note that for lower tolerance values, the above snippet can trigger:

/Users/ogrisel/code/scikit-learn/sklearn/linear_model/_linear_loss.py:867: RuntimeWarning: divide by zero encountered in divide
  fj = self.p[:, i] / (self.q[:, i - 1] + mask)
/Users/ogrisel/code/scikit-learn/sklearn/linear_model/_linear_loss.py:873: RuntimeWarning: invalid value encountered in add
  x[:, i] += fj * x[:, j]

for the newton-lsmr solver. Yet it does not prevent the convergence.

Finally, I think it would be interesting to adapt this benchmark to use benchopt and include it in this panel since it's quite challenging for most solvers yet still realistic enough.

[lorentzenchr]

Out of curiosity, have you tried to profile this to pinpoint the bottlenecks for both the multinomial and non-multinomial cases?

For the multinomial/multiclass case, it clearly is LDL.sqrt_D_Lt_matmul and LDL.L_sqrt_D_matmul in A.matmul and A.rmatmul inside LSMR.

Edit: I was able to significantly speed up those 2 functions in e5f5f48. They are still the bottleneck, but much reduced (~2x).

[lorentzenchr]

With the latest improvements it looks a bit better (btw n_classes=12)

Sparse X (as above)

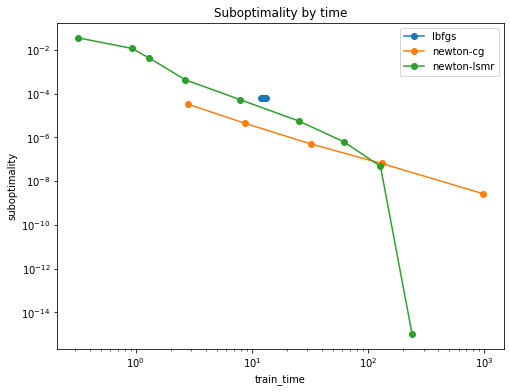
Dense X

Added 24.02.2023

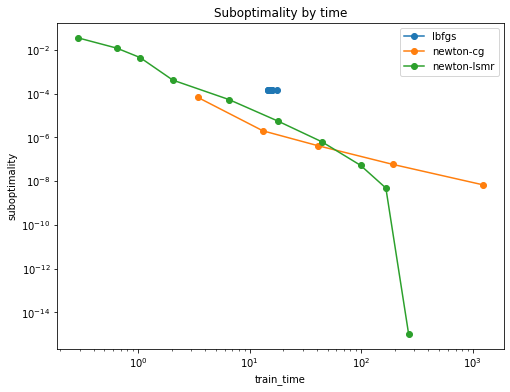
Conclusion

So this solver can be used for very fast but rough estimates or for high precision estimates:smirk:

Code for reproducibility:

import warnings
from pathlib import Path
import numpy as np
from scipy import sparse
from sklearn.compose import ColumnTransformer
from sklearn.datasets import fetch_openml
from sklearn.linear_model import PoissonRegressor, LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model._linear_loss import LinearModelLoss
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
from time import perf_counter
import pandas as pd
import joblib


m = joblib.Memory(location=".", verbose=0)


@m.cache
def prepare_data():
    df = fetch_openml(data_id=41214, as_frame=True, parser='auto').frame
    df["Frequency"] = df["ClaimNb"] / df["Exposure"]
    log_scale_transformer = make_pipeline(
        FunctionTransformer(np.log, validate=False), StandardScaler()
    )
    linear_model_preprocessor = ColumnTransformer(
        [
            ("passthrough_numeric", "passthrough", ["BonusMalus"]),
            (
                "binned_numeric",
                KBinsDiscretizer(n_bins=10, subsample=None),
                ["VehAge", "DrivAge"],
            ),
            ("log_scaled_numeric", log_scale_transformer, ["Density"]),
            (
                "onehot_categorical",
                OneHotEncoder(),
                ["VehBrand", "VehPower", "VehGas", "Region", "Area"],
            ),
        ],
        remainder="drop",
    )
    y = df["Frequency"]
    w = df["Exposure"]
    X = linear_model_preprocessor.fit_transform(df)
    return X, y, w


X, y_orig, w = prepare_data()

print("binning the target...")
binner = KBinsDiscretizer(
    n_bins=300, encode="ordinal", strategy="quantile", subsample=int(2e5), random_state=0
)
y = binner.fit_transform(y_orig.to_numpy().reshape(-1, 1)).ravel().astype(np.int32)

# X = X.toarray()
X_train, X_test, y_train, y_test, w_train, w_test = train_test_split(
    X, y, w, train_size=10_000, test_size=10_000, random_state=0
)
print(f"{X_train.shape = }")
print(f"{sparse.issparse(X_train)=}")
print("y_train.value_counts() :")
print(pd.Series(y_train).value_counts())

results = []
slow_solvers = set()
for tol in np.logspace(-1, -10, 10):
    for solver in ["lbfgs", "newton-cg", "newton-lsmr"]:
        if solver in slow_solvers:
            # skip slow solvers to keep the benchmark runtime reasonable
            continue
        tic = perf_counter()
        # with warnings.catch_warnings():
        #     warnings.filterwarnings("ignore", category=ConvergenceWarning)
        clf = LogisticRegression(
            C=1e12, solver=solver, tol=tol, max_iter=10000
        ).fit(X_train, y_train)
        toc = perf_counter()
        train_time = toc - tic
        if train_time > 200:
            # skip this solver from now on...
            slow_solvers.add(solver)
        # TODO: handle the regularization term...
        train_loss = log_loss(y_train, clf.predict_proba(X_train))
        n_iter = clf.n_iter_[0]
        result = {
            "solver": solver,
            "tol": tol,
            "train_loss": train_loss,
            "train_time": train_time,
            "train_score": clf.score(X_train, y_train),
            "test_score": clf.score(X_test, y_test),
            "n_iter": n_iter,
            "converged": n_iter < clf.max_iter,
        }
        print(result)
        results.append(result)


results = pd.DataFrame.from_records(results)
filepath = Path().resolve() / "bench_multinomial_logistic_regression_mtpl.csv"
results.to_csv(filepath)


import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt


results = pd.read_csv(filepath)
results["suboptimality"] = results["train_loss"] - results["train_loss"].min() + 1e-15
fig, ax = plt.subplots(figsize=(8, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="n_iter", y="suboptimality", loglog=True, marker="o", label=label, ax=ax
    )
ax.set_ylabel("suboptimality")
ax.set_title("Suboptimality by iterations")

fig, ax = plt.subplots(figsize=(8, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="train_time", y="suboptimality", loglog=True, marker="o", label=label, ax=ax
    )
ax.set_ylabel("suboptimality")
ax.set_title("Suboptimality by time")
plt.show()

[ogrisel]

@lorentzenchr I am not sure if you saw but your last push triggered a CI failure. I did not investigate myself but I wanted to make sure that it not go unnoticed.

[lorentzenchr]

Looking at the last plot, I wonder why the LMSR-based solver seems to slow down after the first 4 iterations, before it accelerates in the last two again. Perhaps, the choice of atol in lsmr in the inner_solve could be improved.

[lorentzenchr]

The remaining CI error will be automatically fixed by setting scipy>=1.4, see https://github.com/scipy/scipy/issues/7396. Note that the transpose is only taken in a few tests, the solver itself works fine with those older scipy versions.

[ogrisel]

The remaining CI error will be automatically fixed by setting scipy>=1.4, see https://github.com/scipy/scipy/issues/7396.

For reference, the bump to scipy>=1.4 in main happens in this PR: #24665

[lorentzenchr]

CI all 🟢 again.

[lorentzenchr]

If we want, we could go on and optimize with multi-threaded Cython code like

def sqrt_D_Lt_matmul_cython(
    double[::1, :] x,
    const double[::1, :] p,
    const double[::1, :] q_inv,
    int n_threads=1,
):
    cdef:
        int n_classes = x.shape[1]
        int n_samples = x.shape[0]
        int i, j, k
    for i in range(0, n_classes - 1):  # row i
        # L_ij = -p_i / q_j, we need transpose L'
        for j in range(i + 1, n_classes):  # column j
            for k in prange(n_samples, schedule='static', nogil=True, num_threads=n_threads):
                x[k, i] -= p[k, j] * q_inv[k, i] * x[k, j]
    return np.asarray(x)

This gives a little speed up, but I did not measure the impact on solve. The other bottleneck is coef @ X.T and making this multi-threaded is harder as it calls BLAS routines (dense X) or scipy.sparse routines (scipy decided against openmp).

I think, this solver is still a valuable addition.

[lorentzenchr]

Another benchmark, this time with the 20 newsgroup dataset (vectorized): n_classes=20, n_features=130_107, n_samples=18_846 and sparse X.

import warnings
from pathlib import Path
import numpy as np
from scipy import sparse
from sklearn.datasets import fetch_20newsgroups_vectorized
from sklearn.linear_model import LogisticRegression
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model._linear_loss import LinearModelLoss
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
from time import perf_counter
import pandas as pd


X, y = fetch_20newsgroups_vectorized(subset="all", return_X_y=True)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=0.5, test_size=0.5, random_state=0
)
print(f"{X_train.shape = }")
print(f"{sparse.issparse(X_train)=}")
print(f"n_classes = {len(np.unique(y))}")

results = []
slow_solvers = set()
for tol in np.logspace(-1, -10, 10):
    for solver in ["lbfgs", "newton-cg", "newton-lsmr"]:
        if solver in slow_solvers:
            # skip slow solvers to keep the benchmark runtime reasonable
            continue
        tic = perf_counter()
        # with warnings.catch_warnings():
        #     warnings.filterwarnings("ignore", category=ConvergenceWarning)
        clf = LogisticRegression(
            C=1e12, solver=solver, tol=tol, max_iter=10000
        ).fit(X_train, y_train)
        toc = perf_counter()
        train_time = toc - tic
        if train_time > 200:
            # skip this solver from now on...
            slow_solvers.add(solver)
        # TODO: handle the regularization term...
        train_loss = log_loss(y_train, clf.predict_proba(X_train))
        n_iter = clf.n_iter_[0]
        result = {
            "solver": solver,
            "tol": tol,
            "train_loss": train_loss,
            "train_time": train_time,
            "train_score": clf.score(X_train, y_train),
            "test_score": clf.score(X_test, y_test),
            "n_iter": n_iter,
            "converged": n_iter < clf.max_iter,
        }
        print(result)
        results.append(result)


results = pd.DataFrame.from_records(results)
filepath = Path().resolve() / "bench_multinomial_logistic_regression_mtpl.csv"
results.to_csv(filepath)


import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt


results = pd.read_csv(filepath)
results["suboptimality"] = results["train_loss"] - results["train_loss"].min() + 1e-15
fig, ax = plt.subplots(figsize=(8, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="n_iter", y="suboptimality", loglog=True, marker="o", label=label, ax=ax
    )
ax.set_ylabel("suboptimality")
ax.set_title("Suboptimality by iterations")

fig, ax = plt.subplots(figsize=(8, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="train_time", y="suboptimality", loglog=True, marker="o", label=label, ax=ax
    )
ax.set_ylabel("suboptimality")
ax.set_title("Suboptimality by time")
plt.show()

[lorentzenchr]

After an important improvement in commit e7368e775c5fb5ea34f18022c0141b218d0212a7 that sets a better inner stopping criterion with a forcing sequence like in Newton CG, the benchmarks are looking much better, even impressive!

Edit: The following benchmarks are base on https://github.com/scikit-learn/scikit-learn/pull/25462/commits/3ea7d98e9d82642e36886a850fb7cea55abbd11b.

Poisson Regression with freMTPL2freq dataset

n_features=75, n_samples=542_410 (80% for the training data)

Code for reproducibility:

import warnings
from pathlib import Path
import numpy as np
from scipy import sparse
from sklearn.compose import ColumnTransformer
from sklearn.datasets import fetch_openml
from sklearn.linear_model import PoissonRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model._linear_loss import LinearModelLoss
from sklearn.model_selection import train_test_split
from time import perf_counter
import pandas as pd


def prepare_data():
    df = fetch_openml(data_id=41214, as_frame=True, parser='auto').frame
    df["Frequency"] = df["ClaimNb"] / df["Exposure"]
    log_scale_transformer = make_pipeline(
        FunctionTransformer(np.log, validate=False), StandardScaler()
    )
    linear_model_preprocessor = ColumnTransformer(
        [
            ("passthrough_numeric", "passthrough", ["BonusMalus"]),
            (
                "binned_numeric",
                KBinsDiscretizer(n_bins=10, subsample=None),
                ["VehAge", "DrivAge"],
            ),
            ("log_scaled_numeric", log_scale_transformer, ["Density"]),
            (
                "onehot_categorical",
                OneHotEncoder(),
                ["VehBrand", "VehPower", "VehGas", "Region", "Area"],
            ),
        ],
        remainder="drop",
    )
    y = df["Frequency"]
    w = df["Exposure"]
    X = linear_model_preprocessor.fit_transform(df)
    return X, np.asarray(y), np.asarray(w)


X, y, w = prepare_data()
#X = X.toarray()
X_train, X_test, y_train, y_test, w_train, w_test = train_test_split(
    X, y, w, train_size=0.8, test_size=0.1, random_state=0
)
print(f"{X_train.shape = }")
print(f"{sparse.issparse(X_train)=}")

results = []
loss_sw = w_train / w_train.sum()
slow_solvers = set()
for tol in np.logspace(-1, -11, 11):
    for solver in ["lbfgs", "newton-cholesky", "newton-lsmr"]:
        if solver in slow_solvers:
            # skip slow solvers to keep the benchmark runtime reasonable
            continue
        tic = perf_counter()
        # with warnings.catch_warnings():
        #     warnings.filterwarnings("ignore", category=ConvergenceWarning)
        reg = PoissonRegressor(
            alpha=1e-12,
            solver=solver,
            tol=tol,
            max_iter=10_000 if solver=="lbfgs" else 100,
        ).fit(X_train, y_train, sample_weight=w_train)
        toc = perf_counter()
        train_time = toc - tic
        n_iter = reg.n_iter_
        if train_time > 200 or n_iter >= reg.max_iter:
            # skip this solver from now on...
            slow_solvers.add(solver)
        # Look inside _GeneralizedLinearRegressor to check the parameters.
        # Or run once with verbose=1 and compare to the reported loss.
        train_loss = LinearModelLoss(
            base_loss=reg._get_loss(), fit_intercept=reg.fit_intercept
        ).loss(
            coef=np.r_[reg.coef_, reg.intercept_],
            X=X_train,
            y=y_train,
            l2_reg_strength=reg.alpha,
            sample_weight=loss_sw,
        )
        result = {
            "solver": solver,
            "tol": tol,
            "train_loss": train_loss,
            "train_time": train_time,
            "train_score": reg.score(X_train, y_train),
            "test_score": reg.score(X_test, y_test),
            "n_iter": n_iter,
            "converged": n_iter < reg.max_iter,
        }
        print(result)
        results.append(result)


results = pd.DataFrame.from_records(results)
filepath = Path().resolve() / "bench_poisson_regression_mtpl.csv"
results.to_csv(filepath)


import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt


filepath = Path().resolve() / "bench_poisson_regression_mtpl.csv"

results = pd.read_csv(filepath)
results["suboptimality"] = results["train_loss"] - results["train_loss"].min() + 1e-16

fig, axes = plt.subplots(ncols=2, figsize=(8*2, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="n_iter", y="suboptimality", loglog=True, marker="o", label=label, ax=axes[0]
    )
axes[0].set_ylabel("suboptimality")
axes[0].set_title("Suboptimality by iterations")

for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="train_time", y="suboptimality", loglog=True, marker="o", label=label, ax=axes[1]
    )
axes[1].set_ylabel("suboptimality")
axes[1].set_title("Suboptimality by time")
plt.show()

Multinomial Logistic Regression

freMTPL2freq dataset

n_classes=12, n_features=75, n_samples=10_000 (subsample, dataset is larger)

Sparse X

Dense X

Code for reproducibility:

import warnings
from pathlib import Path
import numpy as np
from scipy import sparse
from sklearn._loss import HalfMultinomialLoss
from sklearn.compose import ColumnTransformer
from sklearn.datasets import fetch_openml
from sklearn.linear_model import PoissonRegressor, LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model._linear_loss import LinearModelLoss
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
from time import perf_counter
import pandas as pd



def prepare_data():
    df = fetch_openml(data_id=41214, as_frame=True, parser='auto').frame
    df["Frequency"] = df["ClaimNb"] / df["Exposure"]
    log_scale_transformer = make_pipeline(
        FunctionTransformer(np.log, validate=False), StandardScaler()
    )
    linear_model_preprocessor = ColumnTransformer(
        [
            ("passthrough_numeric", "passthrough", ["BonusMalus"]),
            (
                "binned_numeric",
                KBinsDiscretizer(n_bins=10, subsample=None),
                ["VehAge", "DrivAge"],
            ),
            ("log_scaled_numeric", log_scale_transformer, ["Density"]),
            (
                "onehot_categorical",
                OneHotEncoder(),
                ["VehBrand", "VehPower", "VehGas", "Region", "Area"],
            ),
        ],
        remainder="drop",
    )
    y = df["Frequency"]
    w = df["Exposure"]
    X = linear_model_preprocessor.fit_transform(df)
    return X, y, w


X, y_orig, w = prepare_data()

print("binning the target...")
binner = KBinsDiscretizer(
    n_bins=300, encode="ordinal", strategy="quantile", subsample=int(2e5), random_state=0
)
y = binner.fit_transform(y_orig.to_numpy().reshape(-1, 1)).ravel().astype(float)

# X = X.toarray()
X_train, X_test, y_train, y_test, w_train, w_test = train_test_split(
    X, y, w, train_size=10_000, test_size=10_000, random_state=0
)
print(f"{X_train.shape = }")
print(f"{sparse.issparse(X_train)=}")
n_classes = len(np.unique(y_train))
print(f"{n_classes=}")
print("y_train.value_counts() :")
print(pd.Series(y_train).value_counts())


results = []
slow_solvers = set()
loss_sw = np.full_like(y_train, fill_value=(1. / y_train.shape[0]))
alpha = 1e-12
for tol in np.logspace(-1, -10, 10):
    for solver in ["lbfgs", "newton-cg", "newton-lsmr"]:
        if solver in slow_solvers:
            # skip slow solvers to keep the benchmark runtime reasonable
            continue
        tic = perf_counter()
        # with warnings.catch_warnings():
        #     warnings.filterwarnings("ignore", category=ConvergenceWarning)
        clf = LogisticRegression(
            C=1/alpha,
            solver=solver,
            tol=tol,
            max_iter=10_000 if solver=="lbfgs" else 1000,
        ).fit(X_train, y_train)
        toc = perf_counter()
        train_time = toc - tic
        n_iter = clf.n_iter_[0]
        if train_time > 200 or n_iter >= clf.max_iter:
            # skip this solver from now on...
            slow_solvers.add(solver)
        # Look inside _GeneralizedLinearRegressor to check the parameters.
        # Or run once with verbose=1 and compare to the reported loss.
        train_loss = LinearModelLoss(
            base_loss=HalfMultinomialLoss(n_classes=n_classes), fit_intercept=clf.fit_intercept
        ).loss(
            coef=np.c_[clf.coef_, clf.intercept_],
            X=X_train,
            y=y_train,
            l2_reg_strength=alpha / X_train.shape[0],
            sample_weight=loss_sw,
        )
        result = {
            "solver": solver,
            "tol": tol,
            "train_loss": train_loss,
            "train_time": train_time,
            "train_score": clf.score(X_train, y_train),
            "test_score": clf.score(X_test, y_test),
            "n_iter": n_iter,
            "converged": n_iter < clf.max_iter,
        }
        print(result)
        results.append(result)


results = pd.DataFrame.from_records(results)
filepath = Path().resolve() / "bench_multinomial_logistic_regression_mtpl_sparse.csv"
results.to_csv(filepath)


import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt


filepath = Path().resolve() / "bench_multinomial_logistic_regression_mtpl_sparse.csv"

results = pd.read_csv(filepath)
results["suboptimality"] = results["train_loss"] - results["train_loss"].min() + 1e-16

fig, axes = plt.subplots(ncols=2, figsize=(8*2, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="n_iter", y="suboptimality", loglog=True, marker="o", label=label, ax=axes[0]
    )
axes[0].set_ylabel("suboptimality")
axes[0].set_title("Suboptimality by iterations")

for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="train_time", y="suboptimality", loglog=True, marker="o", label=label, ax=axes[1]
    )
axes[1].set_ylabel("suboptimality")
axes[1].set_title("Suboptimality by time")
plt.show()

20 newsgroup dataset (vectorized)

n_classes=20, n_features=130_107, n_samples=18_846 and sparse X.

Unpenalized (effectively) => least norm setting

alpha=1e-12

With moderate penalty

alpha=1

Note that for tol <= 1e-08 newton-cg linesearch is failing:

python3.9/site-packages/scipy/optimize/_linesearch.py:306: LineSearchWarning: The line search algorithm did not converge
  warn('The line search algorithm did not converge', LineSearchWarning)
scikit-learn/sklearn/utils/optimize.py:203: UserWarning: Line Search failed
  warnings.warn("Line Search failed")

Code for reproducibility:

import warnings
from pathlib import Path
import numpy as np
from scipy import sparse
from sklearn._loss import HalfMultinomialLoss
from sklearn.datasets import fetch_20newsgroups_vectorized
from sklearn.linear_model import LogisticRegression
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model._linear_loss import LinearModelLoss
from sklearn.model_selection import train_test_split
from time import perf_counter
import pandas as pd


X, y = fetch_20newsgroups_vectorized(subset="all", return_X_y=True)
y = y.astype(float)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=0.5, test_size=0.5, random_state=0
)
print(f"{X_train.shape = }")
print(f"{sparse.issparse(X_train)=}")
n_classes = len(np.unique(y_train))
print(f"{n_classes=}")
print("y_train.value_counts() :")
print(pd.Series(y_train).value_counts())


results = []
slow_solvers = set()
loss_sw = np.full_like(y_train, fill_value=(1. / y_train.shape[0]))
alpha = 1e-12
print(f"l2_reg_strength={alpha/X.shape[0]}")
for tol in np.logspace(-1, -10, 10):
    for solver in ["lbfgs", "newton-cg", "newton-lsmr"]:
        if solver in slow_solvers:
            # skip slow solvers to keep the benchmark runtime reasonable
            continue
        tic = perf_counter()
        # with warnings.catch_warnings():
        #     warnings.filterwarnings("ignore", category=ConvergenceWarning)
        clf = LogisticRegression(
            C=1/alpha, solver=solver, tol=tol, max_iter=10_000 if solver=="lbfgs" else 300
        ).fit(X_train, y_train)
        toc = perf_counter()
        train_time = toc - tic
        n_iter = clf.n_iter_[0]
        if train_time > 200 or n_iter >= clf.max_iter:
            # skip this solver from now on...
            slow_solvers.add(solver)
        # Look inside _GeneralizedLinearRegressor to check the parameters.
        # Or run once with verbose=1 and compare to the reported loss.
        train_loss = LinearModelLoss(
            base_loss=HalfMultinomialLoss(n_classes=n_classes), fit_intercept=clf.fit_intercept
        ).loss(
            coef=np.c_[clf.coef_, clf.intercept_],
            X=X_train,
            y=y_train,
            l2_reg_strength=alpha / X_train.shape[0],
            sample_weight=loss_sw,
        )
        result = {
            "solver": solver,
            "tol": tol,
            "train_loss": train_loss,
            "train_time": train_time,
            "train_score": clf.score(X_train, y_train),
            "test_score": clf.score(X_test, y_test),
            "n_iter": n_iter,
            "converged": n_iter < clf.max_iter,
        }
        print(result)
        results.append(result)


results = pd.DataFrame.from_records(results)
filepath = Path().resolve() / "bench_multinomial_logistic_regression_20newsgroup.csv"
results.to_csv(filepath)


import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt


filepath = Path().resolve() / "bench_multinomial_logistic_regression_20newsgroup.csv"

results = pd.read_csv(filepath)
results["suboptimality"] = results["train_loss"] - results["train_loss"].min() + 1e-16

fig, axes = plt.subplots(ncols=2, figsize=(8*2, 6))
for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="n_iter", y="suboptimality", loglog=True, marker="o", label=label, ax=axes[0]
    )
axes[0].set_ylabel("suboptimality")
axes[0].set_title("Suboptimality by iterations")

for label, group in results.groupby("solver"):
    group.sort_values("tol").plot(
        x="train_time", y="suboptimality", loglog=True, marker="o", label=label, ax=axes[1]
    )
axes[1].set_ylabel("suboptimality")
axes[1].set_title("Suboptimality by time")
plt.show()

Penalty dependence

LSMR

newton-lsmr
alpha=     100.0 train_time=   3.587534 l2_regularization_strength=0.1
alpha=         1 train_time=  23.473143 l2_regularization_strength=0.001
alpha=      0.01 train_time= 208.558041 l2_regularization_strength=1e-05
alpha=    0.0001 train_time=  50.890125 l2_regularization_strength=1.0000000000000001e-07
alpha=     1e-06 train_time= 150.419857 l2_regularization_strength=9.999999999999999e-10
alpha=     1e-08 train_time= 176.927901 l2_regularization_strength=1.0000000000000001e-11
alpha=     1e-10 train_time= 167.058431 l2_regularization_strength=1e-13
alpha=     1e-12 train_time= 146.672581 l2_regularization_strength=1e-15

LSMR A_norm = max(1, n_features/n_sample)

newton-lsmr
alpha=     100.0 train_time=   4.454064 l2_regularization_strength=0.1
alpha=         1 train_time=  28.800517 l2_regularization_strength=0.001
alpha=      0.01 train_time= 186.824286 l2_regularization_strength=1e-05
alpha=    0.0001 train_time= 520.137658 l2_regularization_strength=1.0000000000000001e-07
alpha=     1e-06 train_time= 512.513330 l2_regularization_strength=9.999999999999999e-10
# takes too long

lbfgs

lbfgs
alpha=     100.0 train_time=   9.191765 l2_regularization_strength=0.1
alpha=         1 train_time=  55.298710 l2_regularization_strength=0.001
alpha=      0.01 train_time= 188.124920 l2_regularization_strength=1e-05
alpha=    0.0001 train_time= 358.714925 l2_regularization_strength=1.0000000000000001e-07
alpha=     1e-06 train_time= 654.342208 l2_regularization_strength=9.999999999999999e-10
alpha=     1e-08 train_time= 451.785882 l2_regularization_strength=1.0000000000000001e-11
alpha=     1e-10 train_time= 296.570590 l2_regularization_strength=1e-13
alpha=     1e-12 train_time=  95.537561 l2_regularization_strength=1e-15

import warnings
from pathlib import Path
import numpy as np
from scipy import sparse
from sklearn.datasets import fetch_20newsgroups_vectorized
from sklearn.linear_model import LogisticRegression
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model._linear_loss import LinearModelLoss
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
from time import perf_counter
import pandas as pd


X, y = fetch_20newsgroups_vectorized(subset="all", return_X_y=True)

print("newton-lsmr")
n=1000
for alpha in [1e2, 1, 1e-2, 1e-4, 1e-6, 1e-8, 1e-10, 1e-12]:
    tic = perf_counter()
    LogisticRegression(C=1/alpha, solver="newton-lsmr", tol=1e-4).fit(X[n:,:], y[n:])
    toc = perf_counter()
    train_time = toc - tic
    print(f"{alpha=:10} {train_time=:11f} l2_regularization_strength={alpha/n}")

print("lbfgs")
n=1000
for alpha in [1e2, 1, 1e-2, 1e-4, 1e-6, 1e-8, 1e-10, 1e-12]:
    tic = perf_counter()
    LogisticRegression(C=1/alpha, solver="lbfgs", tol=1e-4, max_iter=10_000).fit(X[n:,:], y[n:])
    toc = perf_counter()
    train_time = toc - tic
    print(f"{alpha=:10} {train_time=:11f} l2_regularization_strength={alpha/n}")

Conclusion

The LSMR-Newton solver can be used for very fast but rough estimates or for high precision estimates. For multinomial logistic regression, at least sufficiently far away from least norm situations, it seems superior to the current solvers.

@rth @TomDLT @agramfort @mathurinm ping in case you are interested.

[ogrisel]

This looks very impressive. However it seems that there are missing results and code snippet for the 20 newsgroups case in the previous comment

[lorentzenchr]

This looks very impressive. However it seems that there are missing results and code snippet for the 20 newsgroups case in the previous comment

On purpose, note the TODO. The 20 newsgroup run takes a lot of time. And I don't find a not fine-tuned LSMR stopping criteria, that works well here. Using a larger penalization would make the problem go away, but the above benchmark I did is close to no penalization in an n_feature > n_samples setting: not so nice for optimizers.

Edit: To give some more details, for n_samples > n_features it seems beneficial to have a short first Newton iteration with only a few inner iterations in LSMR. For the 20 newsgroup setting (with a tiiiiny or no penalization), if the first Newton iteration is stopped early (only a few inner iterations in LSMR), it is a least squares solution and then needs many Newton iterations. If one allows for many inner LSMR iterations in the first Newton iteration, it is solved as solution to Ax=b with much lower loss/objective function and then needs much less Newton iterations in the following.

[jjerphan]

Thank you for those efforts, @lorentzenchr. I am happy that this new solver allows speeding up the resolution by several orders of magnitude both on suboptimality and train time!

I would like to review your work but I hardly have time to for now, unfortunately. :confused:

[ogrisel]

Indeed I also tried 20 newsgroups and I confirm it is very slow with the current state of this PR.

Edit: To give some more details, for n_samples > n_features it seems beneficial to have a short first Newton iteration with only a few inner iterations in LSMR. For the 20 newsgroup setting (with a tiiiiny or no penalization), if the first Newton iteration is stopped early (only a few inner iterations in LSMR), it is a least squares solution and then needs many Newton iterations. If one allows for many inner LSMR iterations in the first Newton iteration, it is solved as solution to Ax=b with much lower loss/objective function and then needs much less Newton iterations in the following.

I think we need to record the number of inner and out iterations and wallclock times for various problems (different shapes, conditioning, loss, regularization strength, sparsity patterns) + tols or maxiter for inner solver and low tols and large maxiter for the outer loop so that we can get a finer insight on a robust strategy to set the lsmr stopping conditions.

[lorentzenchr]

so that we can get a finer insight on a robust strategy to set the lsmr stopping conditions.

Honestly, we don’t have a good infrastructure for that and I spent weeks if not months running benchmarks for estimators, in particular GLMs.

For this particular solver, the n_samples > n_features setting is good, almost according to textbooks. A way to improve would be to introduce another stopping criteria for LSMR either by vendoring or by asking scipy (stop when ||A'r|| <= new_tol, i.e. independent of ||r|| and ||A||, see comments in code). For the underparametrized case, it is also good as long as there is some L2 penalty. The above newsgroup example has practically no penalty and that setting is rarely ever covered for solvers or GLMs (I’m not aware of any publication). I‘m considering to make the initial atol smaller for exactly this setting, dependent on the penalty. A commit might follow with an update of the the above benchmarks (in the same github comment).

[lorentzenchr]

For GLMs with non-canonical link functions (e.g. Gamma and Tweedie with p > 1, the log link is not the canonical link) the Hessian is not equal to the FIM and therefore not guaranteed to be Positive Definite.

Is LSMR somehow robust to this? Or can this cause the solver to diverge? Or do we just fallback to LBFGS in that case?

Note: this cannot happen for logistic regression since the logit link (inverse logistic sigmoid) is canonical and the Hessian is Positive Definite as long as the predictions are not overconfident (exactly 0 or 1)

Note that this problem should already happen with `"newton-cholesky"`` without me realizing but the LFBGS fallback probably might hide it without me realizing. I wonder if you have specifically investigated this for Gamma regression with logit links @lorentzenchr.

All the glm tests with fixture glm_dataset also run a GammaRegressor. LSMR also falls back to LBFGS in certain cases, but I did not investigate or was not yet able to trigger such a case.

[lorentzenchr]

Commit https://github.com/scikit-learn/scikit-learn/pull/25462/commits/83ce34fc7a528f096718bfff03f07d94253d3b0b passes SKLEARN_TESTS_GLOBAL_RANDOM_SEED="all" pytest -n auto -rfE sklearn/linear_model/_glm/tests/test_glm.py locally on my laptop.

[ogrisel]

When trying to trigger the LBFGS fallback by trying to make the model extremely confident so has to make the Hessian numerically degenerate I triggered the following ZeroDivisionError at iteration 26 instead:

File ~/code/scikit-learn/sklearn/linear_model/_glm/_newton_solver.py:974 in inner_solve
    atol=eta * norm_G / (self.A_norm * self.r_norm),
ZeroDivisionError: float division by zero

>>> import numpy as np
... from sklearn.linear_model import LogisticRegression
... 
... x = np.array([-1e24] * 1 + [1e24] * 1)
... X = x.reshape(-1, 1)
... y = (x > 0).astype(np.int32)
... 
... lr = LogisticRegression(solver="newton-lsmr", penalty=None, verbose=100).fit(X, y)
... lr.n_iter_
[...]
Newton iter=26
    norm(gradient) = 4170877078229.1255
Traceback (most recent call last):
  Cell In[2], line 8
    lr = LogisticRegression(solver="newton-lsmr", penalty=None, verbose=100).fit(X, y)
  File ~/code/scikit-learn/sklearn/base.py:1148 in wrapper
    return fit_method(estimator, *args, **kwargs)
  File ~/code/scikit-learn/sklearn/linear_model/_logistic.py:1321 in fit
    fold_coefs_ = Parallel(n_jobs=self.n_jobs, verbose=self.verbose, prefer=prefer)(
  File ~/code/scikit-learn/sklearn/utils/parallel.py:65 in __call__
    return super().__call__(iterable_with_config)
  File ~/mambaforge/envs/dev/lib/python3.11/site-packages/joblib/parallel.py:1085 in __call__
    if self.dispatch_one_batch(iterator):
  File ~/mambaforge/envs/dev/lib/python3.11/site-packages/joblib/parallel.py:901 in dispatch_one_batch
    self._dispatch(tasks)
  File ~/mambaforge/envs/dev/lib/python3.11/site-packages/joblib/parallel.py:819 in _dispatch
    job = self._backend.apply_async(batch, callback=cb)
  File ~/mambaforge/envs/dev/lib/python3.11/site-packages/joblib/_parallel_backends.py:208 in apply_async
    result = ImmediateResult(func)
  File ~/mambaforge/envs/dev/lib/python3.11/site-packages/joblib/_parallel_backends.py:597 in __init__
    self.results = batch()
  File ~/mambaforge/envs/dev/lib/python3.11/site-packages/joblib/parallel.py:288 in __call__
    return [func(*args, **kwargs)
  File ~/mambaforge/envs/dev/lib/python3.11/site-packages/joblib/parallel.py:288 in <listcomp>
    return [func(*args, **kwargs)
  File ~/code/scikit-learn/sklearn/utils/parallel.py:127 in __call__
    return self.function(*args, **kwargs)
  File ~/code/scikit-learn/sklearn/linear_model/_logistic.py:485 in _logistic_regression_path
    w0 = sol.solve(X=X, y=target, sample_weight=sample_weight)
  File ~/code/scikit-learn/sklearn/linear_model/_glm/_newton_solver.py:426 in solve
    self.inner_solve(X=X, y=y, sample_weight=sample_weight)
  File ~/code/scikit-learn/sklearn/linear_model/_glm/_newton_solver.py:974 in inner_solve
    atol=eta * norm_G / (self.A_norm * self.r_norm),
ZeroDivisionError: float division by zero

We might need a np.max(self.A_norm * self.r_norm, np.finfo(dtype).eps) of similar here.

[ogrisel]

Also note that "newton-cholesky" and "lbfgs" converge with n_iter_ = [0]. "newton-cg" converges with n_iter_ = [64] on this problem.

[ogrisel]

Actually there is a problem with lbfgs on the above problem, it does not converge:

ABNORMAL_TERMINATION_IN_LNSRCH                              

 Line search cannot locate an adequate point after MAXLS
  function and gradient evaluations.
  Previous x, f and g restored.
 Possible causes: 1 error in function or gradient evaluation;
                  2 rounding error dominate computation.
/Users/ogrisel/code/scikit-learn/sklearn/linear_model/_logistic.py:459: ConvergenceWarning: lbfgs failed to converge (status=2):
ABNORMAL_TERMINATION_IN_LNSRCH.

Increase the number of iterations (max_iter) or scale the data as shown in:
    https://scikit-learn.org/stable/modules/preprocessing.html
Please also refer to the documentation for alternative solver options:
    https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
  n_iter_i = _check_optimize_result(

and

>>> lr.coef_
array([[0.]])

while "newton-cholesky" does converge on this toy yet extreme problem.

I don't know if the failure of lbfgs here should be considered a bug or not but since lbfgs is our robust fallback, this might be a problem :) Maybe LBFGS should try a simple gradient step when the line search fails?

[ogrisel]

I found a way to trigger the LBFGS fallback for the multiclass case:

import numpy as np
from sklearn.linear_model import LogisticRegression

x = np.array([-1e24] * 1 + [1e24] * 2)
X = x.reshape(-1, 1)
y = np.asarray([0, 1, 2])

lr = LogisticRegression(solver="newton-lsmr", penalty=None, verbose=100).fit(X, y)

[lorentzenchr]

I opened #26707 for investigating the inner solver stopping criterion and run a log of benchmarks. There is no clear winner. I have to leave it as is: Either it is good enough in it's current shape or someone else needs to dig deeper.

My conclusion is that we have quite some room of improvement of the current solvers, like #24752. Also the "newton-cg" could likely be improved by doing what liblinear does, see Galli & Lin "A Study on Truncated Newton Methods for Linear Classification" (https://www.csie.ntu.edu.tw/~cjlin/papers/tncg/tncg.pdf or https://doi.org/10.1109/TNNLS.2020.3045836). Currently, I'm not 100% convinced of the newton-lsmr, but it is such a nice solver for multiclass problems!

[github-actions[bot]]

✔️ Linting Passed

All linting checks passed. Your pull request is in excellent shape! ☀️

_{Generated for commit: 71d2733. Link to the linter CI: here}

[ogrisel]

Currently, I'm not 100% convinced of the newton-lsmr, but it is such a nice solver for multiclass problems!

There are cases where it's indeed quite impressive based on the last benchmarks that are now collapsed in the discussion.

https://github.com/scikit-learn/scikit-learn/pull/25462#issuecomment-1575538110

But I agree that fixing #24752 would be helpful to get a clearer picture.

Also based on benchopt, it seems that SAG & SAGA are better reference solvers for 20 newsgroups, see e.g.:

https://benchopt.github.io/results/preprint_results_preprint_results_logreg_l2.html

I have no intuition on why this should be the case.

You'll have to switch the dataset in the menu on the left to see the results on 20 newsgroups.

UPDATE: actually the results on this dataset are completely different with and without scaling.