NaNs in V_IJ

[ericmjl]

On a toy problem, in which I am using Random Forests + ForestCI to prototype some ideas, I will randomly get NaNs in the V_IJ estimates.

This toy problem is using a random forest to fit a 1D curve. Code to try reproducing the problem is below.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from forestci import random_forest_error

def func(x):
    return x**2 + 3*x - 3

x_train = np.hstack([np.linspace(-10, -3, 10), np.linspace(3, 10, 10)])
x_test = np.linspace(-10, 10, 1000)

fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(20, 8))


for i in range(10):
    rfr = RandomForestRegressor(n_estimators=100, n_jobs=1)
    rfr.fit(x_train.reshape(-1, 1), func(x_train))
    preds = rfr.predict(x_test.reshape(-1, 1))
    var_est = random_forest_error(rfr, 
                                  x_train.reshape(-1, 1), 
                                  x_test.reshape(-1, 1), 
                                  calibrate=True)
    axes.flatten()[i].errorbar(x_test, preds, yerr=var_est)

I noticed two observations. Firstly, the estimated errors are unstable. Please see image below.

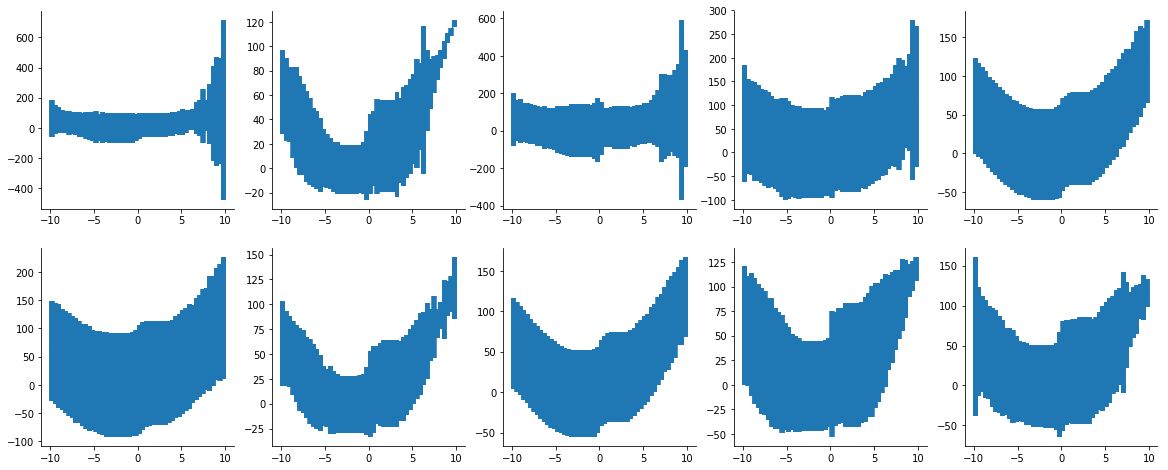
Is this a result of having few training samples (only 20 observations on the curve)? Or is there something else I'm missing conceptually?

Secondly, I will occasionally get NaNs in var_est (the estimate of V_IJ), hence the errors are unplottable.

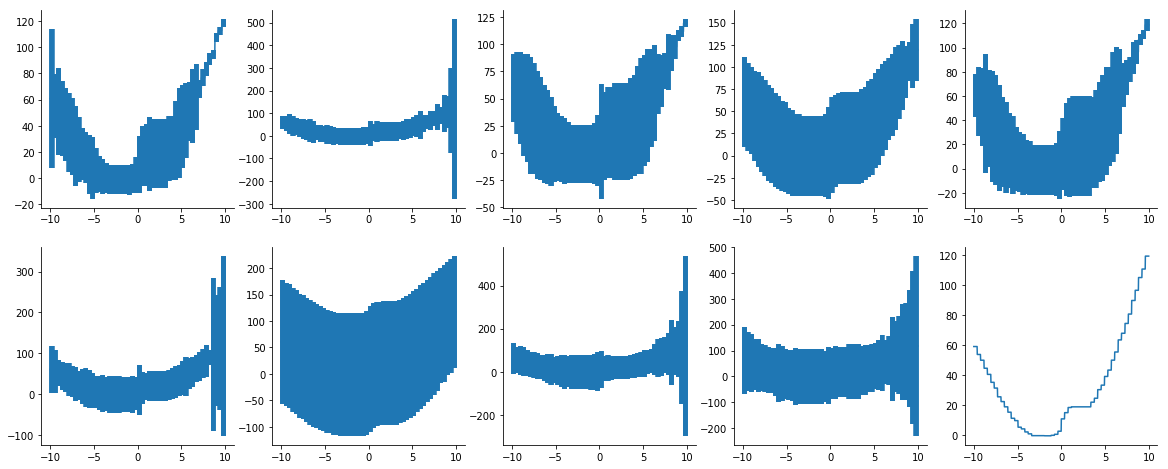
I'm not quite sure how to diagnose what is happening here. Would you guys be able to provide some input on where I might be doing something wrong?

[MillHaus33]

I have faced a similar issue. I have a target variable with a long right tail. If I cap my target variable the forest error does not have missing values. As I raise my target variable cap the missing variables increase. Any insight as to why this issue occurs would be useful! Thanks!

[hermanc1]

We are having the same problem. Has anyone found a solution to this?

[lcol90]

Is there any solution for this problem? My NaNs seem to derive from eb_prior = gfit(variances, sigma) in calibrateEB. Thanks in advance!

[DavidLloydNGP]

Similar to @MillHaus33 I see this problem with a target variable with a long-tailed distribution (or more specifically, quite a few large value outliers). The problem appears for certain test/train splits, so it's the case that the distribution of the target variable always causes the problem. From a practical point of view, there may some kind of data transformation that doesn't impair the model performance but also avoids this problem. I have not found evidence to support this yet though.