implement SpendN, OutputN actions

[redshiftzero]

Suggestion from @hdevalence:

it would be useful to work out how much space saving we could get by having Spend2 and Output2 actions

Similarly for Spend2, Spend4, etc.

Edit: Based on the results below, it makes sense to implement SpendN, OutputN actions where the smallest N is 2. These actions will replace Spend and Output. This makes sense to begin once the Groth16 proofs are implemented.

[redshiftzero]

SpendN

Costs in size per Spend:

• 1 proof (iirc Groth16 proofs are constant size, and I believe are 3 group elements so let’s say 192 bytes)
• 1 auth signature = 64 bytes
• 1 balance commitment = 32 bytes
• 1 nullifier = 32 bytes
• 1 rk = 32 bytes Total cost: 352 bytes for a single Spend

For what follows I assume we share the rk, auth sig, and proof between the N spends.

Cost for a Spend2:

• Shared proof, auth signature, and rk: 288 bytes total
• 2 nullifiers = 64 bytes
• ~2~ 1 balance commitment = 32 bytes Total cost: 384 bytes

So:

• the cost in bytes for a SpendN = 320 + N * (32)
• the savings of SpendN over N * Spends = N * 352 - 320 - N * 32
  • so for N=2: there is a 704-320-64 = 320 byte savings

OutputN

Costs per Output:

• 1 proof, 192 bytes
• Note commitment = 32 bytes
• Ephemeral public key = 32 bytes
• Encrypted note = 168 bytes
• Balance commitment = 32 bytes
• ovk_wrapped_key = 48 bytes
• wrapped_memo_key = 48 bytes Total cost: 552 bytes

Cost per Output2:

• Shared proof, 192 bytes
• 2 Note commitment = 2 * 32 bytes
• 2 Ephemeral public key = 2 * 32 bytes
• 2 Encrypted note = 2 * 168 bytes
• ~2~ 1 balance commitment = 32 bytes
• 2 ovk_wrapped_key = 2 * 48 bytes
• 2 wrapped_memo_key = 2 * 48 bytes Total cost: 880 bytes

So:

• the cost in bytes for an OutputN = 224 + N * (328)
• the savings of OutputN over N * Outputs = N * 552 - 224 - N * 328
  • so for N=2: there is a 1104 - 224 - 656 = 224 byte savings

[hdevalence]

2 balance commitments

Do we need multiple balance commitments? Since the balance commitments can commit to arbitrary value vectors, I think we could have just one per action, committing to the sum of all of the spends and outputs.

[redshiftzero]

ah true! I've updated the calculations above to only use a single balance commitment per ActionN and corrected the size of a Groth16 proof (each proof is two G1 elements (48 bytes compressed), one G2 element (96 bytes compressed), which are 192 bytes in total). Here's a plot showing the savings of ActionN over N actions in bytes:

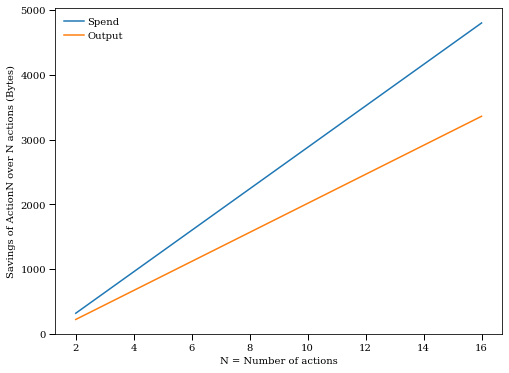
Savings are better for the spends, for N=16 we get a savings of 4800 bytes for spends, 3360 bytes for outputs.

[hdevalence]

We should backburner this until after we have fee mechanics, which would inform our choices about what's worth implementing. But it seems likely that we'll get more upside out of SpendN than OutputN, because high-arity spend statements allow more economically sweeping dust value.

[hdevalence]

We won't be doing this because we're already partway through our proof ceremony.