Faces from edges?

[Sentient07]

Hello Mike,

I was wondering if it would be possible to have a mesh w/o orientation if given edges and vertices? i.e, can I create trimesh.Trimesh w/o face but edges (as indices or adjacency and position) ? Thanks!

Edit: related to this https://github.com/mikedh/trimesh/issues/1071 but not the same as you already have a Trimesh instance.

[mikedh]

Hey, you'd have to create triangular faces to use it in Trimesh. I'm not sure how to do this well or if it's a well-defined problem but you might use cycles as a starting point:

import os
import trimesh
import numpy as np

import networkx as nx


def fan(p):
    """
    Convert a 1D array of indexes into an
    (n, 3) triangle fan indexes.
    """
    if len(p) == 3:
        return [p]
    return [[p[0], p[i], p[i + 1]] for i in range(1, len(p) - 1)]


if __name__ == '__main__':

    # try to reconstruct a box
    m = trimesh.creation.box()

    e = m.edges_unique.copy()
    v = m.vertices.copy()

    # find connected loops of these edges
    cycles = nx.cycle_basis(nx.from_edgelist(e))

    # generate a triangle fan for each cycle
    f_recon = np.vstack([fan(c) for c in cycles])

    # make a bad mesh with more faces than the original
    mesh_bad = trimesh.Trimesh(v, f_recon)

Or you could load the edges as a Path3D:

In [5]: trimesh.load_path(v[e])
Out[5]: <trimesh.Path3D(vertices.shape=(8, 3), len(entities)=12)>

[Kiord]

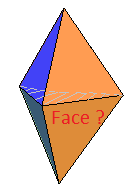
I agree that this problem is not very well defined since three vertices connected by an edge do not necessarily form a face. For example, this hexahedron :

Another solution is to use the adjacency block matrix of the bipartite graph vertices ⟷ edges. 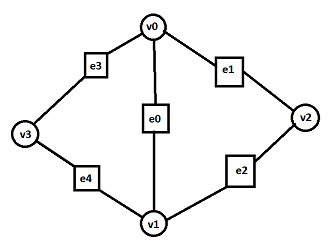(square nodes and circle nodes represent edges and vertices, respectively)

The adjacency matrix of a graph to the power p contains the number of paths of length p linking two nodes of the graph. In your case you search for the 3rd vertex to complete each edge to make a face of it. These vertices are 3 nodes apart from the edge of interest e0 :

e0 ⟷ v0 ⟷ e1 ⟷ v2
e0 ⟷ v1 ⟷ e2 ⟷ v2
e0 ⟷ v0 ⟷ e3 ⟷ v3
e0 ⟷ v1 ⟷ e4 ⟷ v3

Since the graph is not directed, there are 4 paths that link e0 to v2 and 4 other paths that link e0 to v3. So the coordinates where the adjacency block matrix to the power p=3 is equal to 4 are what we look for. The issue is that it gives us many times the same faces, and we have to manually delete the redundant ones.

# (Considering you have vertices and edges as np.ndarrays)
# Bipartite graph adjacency block matrix
row = np.repeat(np.arange(len(edges)), 2) # Two vertices by edge
col = edges.flat # Column index = vertex id
data = np.ones_like(row)
EV = sparse.coo_matrix((data, (row, col)), shape=(len(edges), len(vertices))).tocsr() # EV stands for Edges⟷Vertices

# To the power 3 
EV_3 = EV * EV.T * EV # Adjacency block matrix is not square

# Extract the coordinates where == 4
EV_face = (EV_3 == 4).tocoo() # coo to have a nice data/row/col format

# Complete the edges
edges_to_complete =  edges[EV_face.row]
faces = np.concatenate((edges_to_complete , EV_face.col[:, None]), axis=1)

# Clean the faces
faces = np.unique(np.sort(faces, axis=1), axis=0) # should be possible to optimize...