Any good way to find boundary points of a mesh?

[YuanWenqing]

I want to find boundary points of a 3D mesh and an estimated padding can be applied to ignore small holes or "close-enough" distances among disconnected faces.

I tried trimesh.polygons.projected to project 3D mesh into 2D polygons and then handling it in 2D via shapely. But for some mesh, projection is incorrect. Does anyone know a better way?

mesh: model.obj.zip

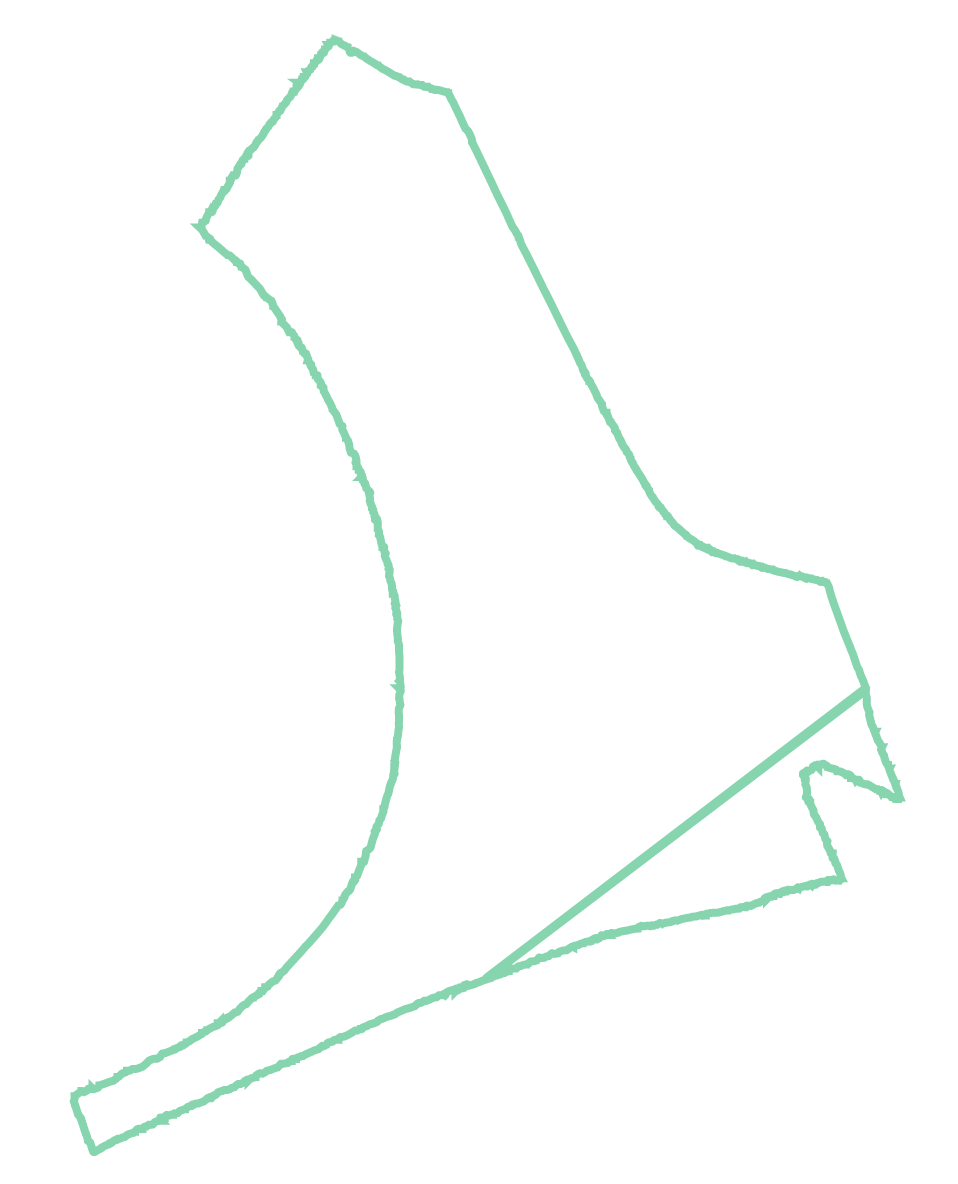
shapely boundary (some faces is REMOVED):

This model consists two parts and for each part boundary is nearly correct.

[MarcelHeu]

you could use the following function to get a concave or the convex hull (depending on the alpha parameter):

import numpy as np

from shapely.geometry import MultiLineString
from shapely.ops import unary_union, polygonize
from scipy.spatial import Delaunay
from collections import Counter
import itertools

"Function to do calculate the concave hull fast"
def concave_hull(input):  # coords is a 2D numpy array
    
    coords  = input[0]
    alpha   = input[1]
    
    if alpha <= 0:
        alpha = 0.001

    # i removed the Qbb option from the scipy defaults.
    # it is much faster and equally precise without it.
    # unless your coords are integers.
    # see http://www.qhull.org/html/qh-optq.htm
    tri = Delaunay(coords, qhull_options="Qc Qz Q12").vertices

    ia, ib, ic = (
        tri[:, 0],
        tri[:, 1],
        tri[:, 2],
    )  # indices of each of the triangles' points
    pa, pb, pc = (
        coords[ia],
        coords[ib],
        coords[ic],
    )  # coordinates of each of the triangles' points

    a = np.sqrt((pa[:, 0] - pb[:, 0]) ** 2 + (pa[:, 1] - pb[:, 1]) ** 2)
    b = np.sqrt((pb[:, 0] - pc[:, 0]) ** 2 + (pb[:, 1] - pc[:, 1]) ** 2)
    c = np.sqrt((pc[:, 0] - pa[:, 0]) ** 2 + (pc[:, 1] - pa[:, 1]) ** 2)

    s = (a + b + c) * 0.5  # Semi-perimeter of triangle

    area = np.sqrt(
        s * (s - a) * (s - b) * (s - c)
    )  # Area of triangle by Heron's formula

    filter = (
        a * b * c / (4.0 * area) < 1.0 / alpha
    )  # Radius Filter based on alpha value

    # Filter the edges
    edges = tri[filter]

    # now a main difference with the aforementioned approaches is that we dont
    # use a Set() because this eliminates duplicate edges. in the list below
    # both (i, j) and (j, i) pairs are counted. The reasoning is that boundary
    # edges appear only once while interior edges twice
    edges = [
        tuple(sorted(combo)) for e in edges for combo in itertools.combinations(e, 2)
    ]

    count = Counter(edges)  # count occurrences of each edge

    # keep only edges that appear one time (concave hull edges)
    edges = [e for e, c in count.items() if c == 1]

    # these are the coordinates of the edges that comprise the concave hull
    edges = [(coords[e[0]], coords[e[1]]) for e in edges]

    # use this only if you need to return your hull points in "order" (i think
    # its CCW)
    ml      = MultiLineString(edges)
    poly    = polygonize(ml)
    hull    = unary_union(list(poly))
    
    if hasattr(hull, 'geoms'):
        hull_vertices  = [list(x.exterior.coords.xy) for x in hull.geoms]
    else:
        hull_vertices = [hull.exterior.coords.xy]
    
    while not hull_vertices:
        hull_vertices = concave_hull([coords,alpha-0.5])

    return hull_vertices

projection = mesh.vertices[:,:2]
alpha = 1.0 # if alpha == 0 --> calculate convex hull
coordinates = concave_hull([projection,alpha])

x = coordinates[0][0] 
y = coordinates[0][1]

[mikedh]

Have you looked at mesh.outline?

[YuanWenqing]

Have you looked at mesh.outline?

Yeah, I tried mesh.outline too. But if mesh is composed by parts which are close to each other but not connected, mesh.outline gives multiple lines. It seems no args to ignore small holes or close gaps. I tried to link these lines but lines are inconsistent in line order and point order. Adjacent lines are not neighbors in outline.entities. And some lines have points in order of clockwise but others counter-clockwise.

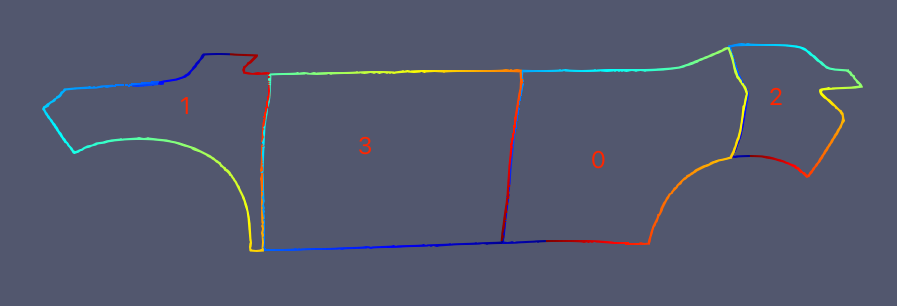The point order in line is implies by the color in jet colorspace(cold blue to hot red).

[mikedh]

Yeah I think there's no way of avoiding implementing a custom distance-based linker to do that. I might try computing the vector-along-the-segment from the outline, and doing a scipy.spatial.cKDTree query which considers vertex distance and direction, followed by a mesh.update_vertices?

[YuanWenqing]

@mikedh you're right! I implemented a custom linker to do that. It may be helpful in my case but not general enough. Look forward to your update.