fix 369

[briochemc]

trafficstars

• [x] Closes #369
• [ ] Tests added
• [ ] Passes pre-commit run --all-files
• [ ] User visible changes (including notable bug fixes) are documented in whats-new.rst
• [ ] New functions/methods are listed in api.rst

[review-notebook-app[bot]]

Check out this pull request on 

See visual diffs & provide feedback on Jupyter Notebooks.

---

Powered by ReviewNB

[jbusecke]

Thanks @briochemc. This is helpful but also potentially breaking peoples code. I am planning to do another deep dive on the vertex order (to solve e.g. #368 ) and will try to ship this with any other updates as a major update!

[briochemc]

BTW not sure If I'm completely misunderstanding what you are planning, but I've been thinking a tiny bit about these vertex orders (I need it in some of my work to detect where the seam is), and I think it would be better to check which vertices match between neighbouring cells, rather than looking at the order of lat and lon values themselves. That way, the order should be consistently set such that, for any grid cell (i,j) not on the border:

• its 2nd vertex = the 1st vertex of the (i+1,j) neighbour (to the "east")
• its 3rd vertex = the 4th vertex of the (i+1,j) neighbour (to the "east")
• its 3rd vertex = the 2nd vertex of the (i,j+1) neighbour (to the "north")
• its 4th vertex = the 1st vertex of the (i,j+1) neighbour (to the "north")

If I take this CF-conventions image (which has the order of dimensions for i and j swapped): 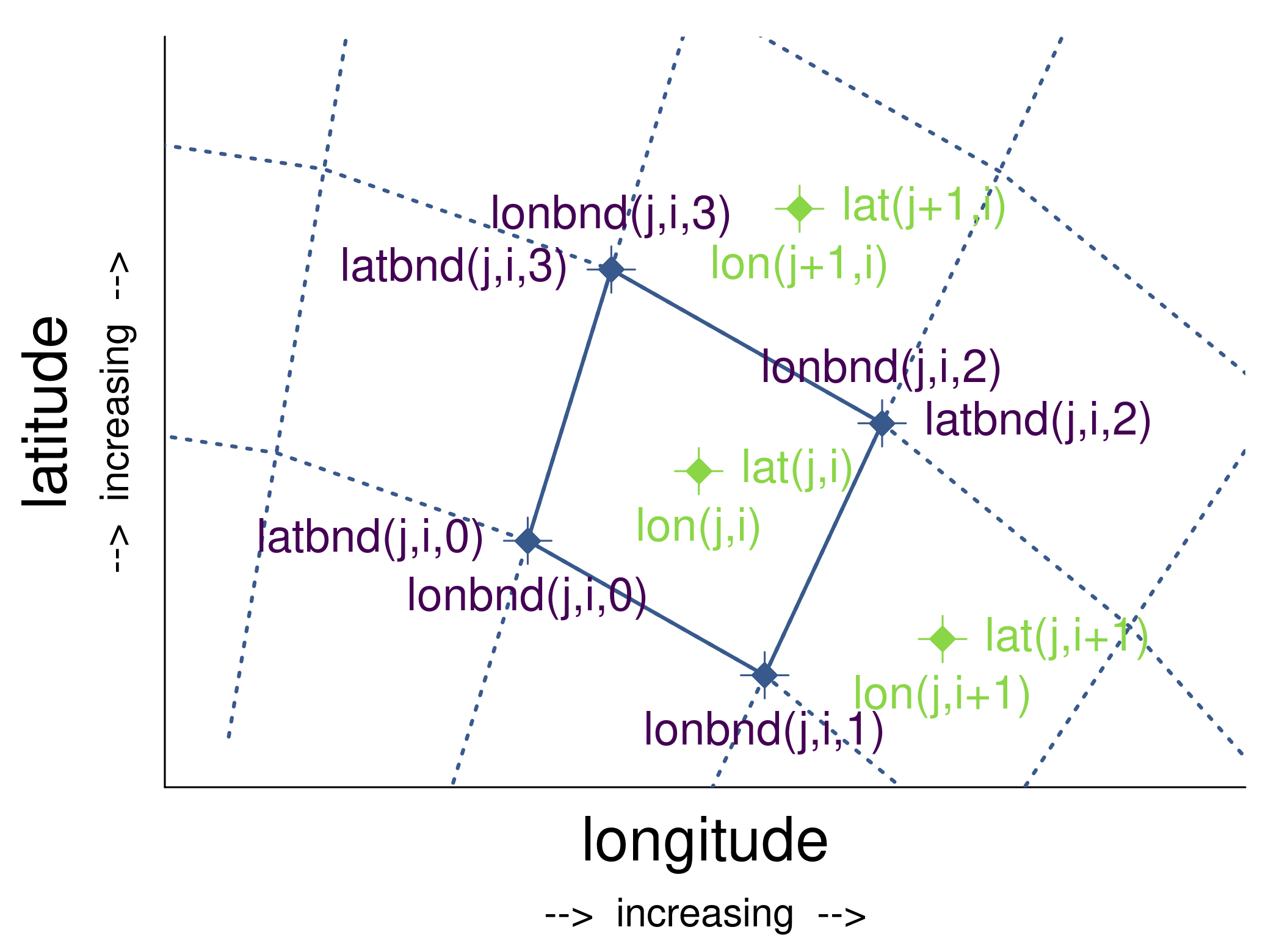it would mean checking that

# (i,j) 2nd vertex = (i+1,j) 1st vertex
lonbnd[j, i, 1] == lonbnd[j, i+1, 0]
latbnd[j, i, 1] == latbnd[j, i+1, 0]
# (i,j) 3rd vertex = (i+1,j) 4th vertex
lonbnd[j, i, 2] == lonbnd[j, i+1, 3]
latbnd[j, i, 2] == latbnd[j, i+1, 3]
# (i,j) 3rd vertex = (i,j+1) 2nd vertex
lonbnd[j, i, 2] == lonbnd[j+1, i, 1]
latbnd[j, i, 2] == latbnd[j+1, i, 1]
# (i,j) 4th vertex = (i,j+1) 1st vertex
lonbnd[j, i, 3] == lonbnd[j+1, i, 0]
latbnd[j, i, 3] == latbnd[j+1, i, 0]

And any other "matching vertex" for cells on the borders would indicate a connection (e.g., periodic wrapping along lon) or a seam, if any (at the north/south poles). Does that make sense?

[jbusecke]

That is a smart way to test the consistency. I think this is implicitly ensured in my hacky solution in https://github.com/jbusecke/xMIP/issues/368#issuecomment-2289934489, but I will definitely try to use that part of the logic over there.

[briochemc]

In case this helps your implementation in xmip, I have implemented my own in Julia in OceanTransportMatrixBuilder.jl in a slightly different way, which I think is clearer. I just intersect the set of vertices of cells (i,j), (i+1,j), and (i,j+1) to determine the vertex index order. Code is located here and looks like this (with 1-indexing in Julia):

# The default orientation is the following:
#
#     4 ────┐ 3
#           │
#     1 ────┘ 2
#
# Given lon_vertices and lat_vertices, find the permutation
# that sorts the vertices in that order.
function vertexpermutation(lon_vertices, lat_vertices)
    # Make sure the vertices are in the right shape (4, nx, ny)
    @assert size(lon_vertices, 1) == size(lat_vertices, 1) == 4
    # Take the first grid cell
    i = j = 1
    # Turn the vertices into points
    points = collect(zip(lon_vertices[:, i, j], lat_vertices[:, i, j]))
    points_east = collect(zip(lon_vertices[:, i+1, j], lat_vertices[:, i+1, j]))
    points_north = collect(zip(lon_vertices[:, i, j+1], lat_vertices[:, i, j+1]))
    # Find the common points
    common_east = intersect(Set(points), Set(points_east))
    common_noth = intersect(Set(points), Set(points_north))
    # Find the indices of the common points
    idx_east = findall(in(common_east), points)
    idx_north = findall(in(common_noth), points)
    idx3 = only(intersect(idx_east, idx_north)) # common to all 3 cells
    idx2 = only(setdiff(idx_east, idx3)) # common to (i,j) and (i+1,j) only
    idx4 = only(setdiff(idx_north, idx3)) # common to (i,j) and (i,j+1) only
    idx1 = only(setdiff(1:4, idx2, idx3, idx4)) # only in (i,j)
    return [idx1, idx2, idx3, idx4]

end

Visual check part of my local tests for my sanity that may be a helpful illustration: