imuncle.github.io
 imuncle.github.io copied to clipboard
imuncle.github.io copied to clipboard
大叔的个人小站
对于四足机器人这个整体来说,需要关注六个物理量:`三轴欧拉角`以及`前后、左右、旋转`三个速度,我们要做的就是使用遥控器控制这六个物理量,然后机器人将这六个物理量转换为12个舵机的角度值。 这篇文章将解决三轴欧拉角的转换问题,即四足机器人的姿态解析。 # yaw轴解析 考虑如下模型 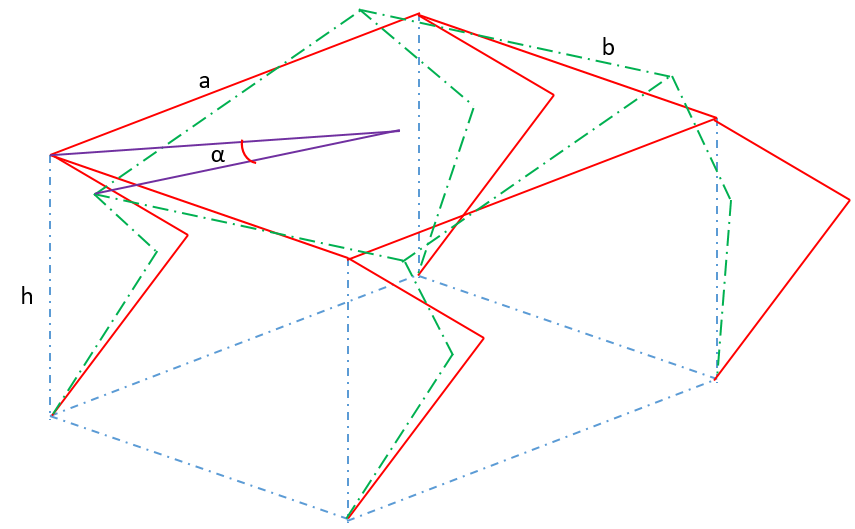 上图中红色线框是原本的位置,绿色虚线框是水平偏转α后的位置,显然四条腿的变化都是一样的,任选一条腿分析就行。现选取上图中最左侧的那一条腿进行分析。 俯视图如下 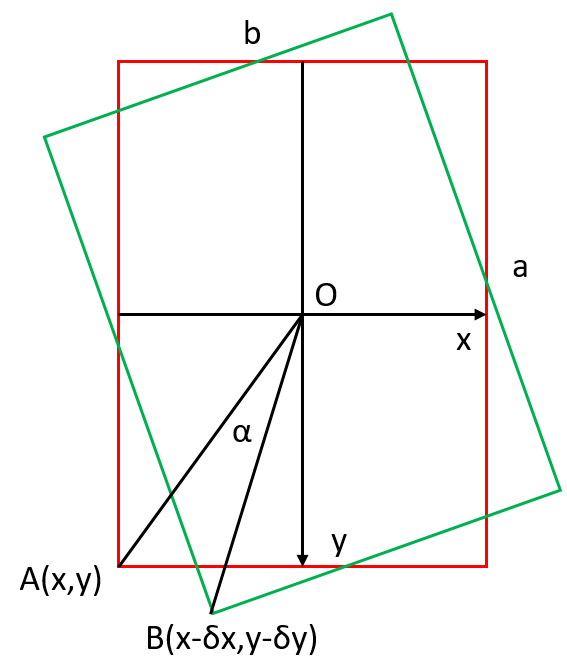 显然,只需要求得δx和δy就行了,因为对于这一个关节来说,腿部的末端移动量就是δx和δy,图中使用-δx和-δy的原因是两者的坐标系不同,参考系不同。 已知四足机器人的长为a,宽为b,AO与y轴的夹角可以事先计算出来,是一个定值,记为θ,AO长度也是一个定制,记为L,那么有以下等式 $$\begin{cases} x=\frac{b}{2}\\\ y=\frac{a}{2}\\\ x-\delta x=L\sin (\theta-\alpha)\\\ y-\delta y=L\cos (\theta-\alpha)\\\ \end{cases} $$ 可求出δx和δy的值 $$\begin{cases} \delta x=\frac{b}{2}-L\sin (\theta-\alpha)\\\ \delta y=\frac{a}{2}-L\cos (\theta-\alpha)\\\...
今天在改进博客的时候遇到一个问题。我的部分代码如下: ```javascript for(var i in config.icons) { document.getElementById('footer').innerHTML += ''; if(config.icons[i].hidden_img != undefined && config.icons[i].hidden_img != null) { $('#icon_'+i).mouseover(function() { footer.changeIcon(i, 'show'); }); $('#icon_'+i).mouseout('onmouseout', function() { footer.changeIcon(i, 'hidden'); }); }...
云台是个好东西,走到哪里都希望有一个,看起来舒服。 先祭出两张图   啊,太炫酷了,所以我也想给我的四足机器人加一个云台(狗头),就像spotMini这种,有四个自由度。 # 狗头移动算法 最基础的还是要实现“狗头”的位置控制,这个和前面说的腿部的控制非常相似,甚至可以说是一模一样,抽象模型如下 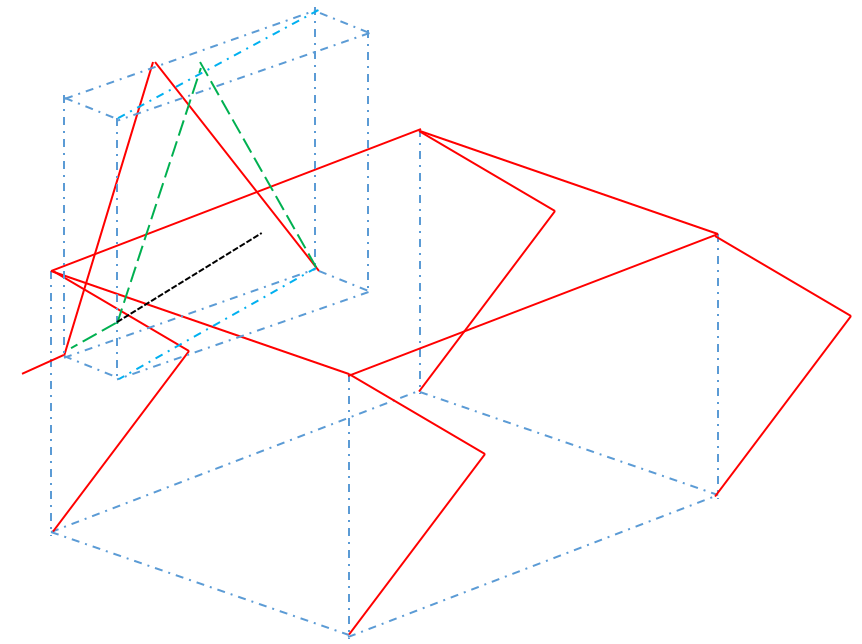 好了,不多说,参考[四足机器人制作(一) 腿部运动算法](https://imuncle.github.io/content.html?id=61),解三角函数就完事了。 # 狗头稳定 首先要明确,我们想实现狗头稳定在一点需要获得机器人的哪些信息,考虑下面这幅图 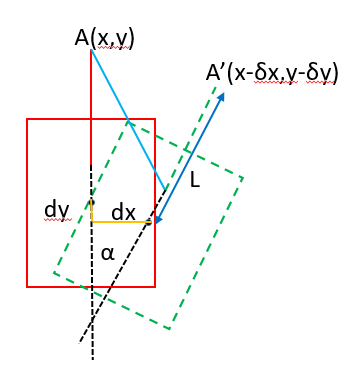 显然,和腿部控制类似,我们只需要求得δx和δy,就可以在机器人身体移动之后,控制狗头回到之前的位置,也就是“固定”在原地。 要求得δx和δy,我们就需要求得机器人的位移dx和dy,机器人的偏转角度α,然后通过三角函数计算得到δx和δy。 同样的从另一侧看 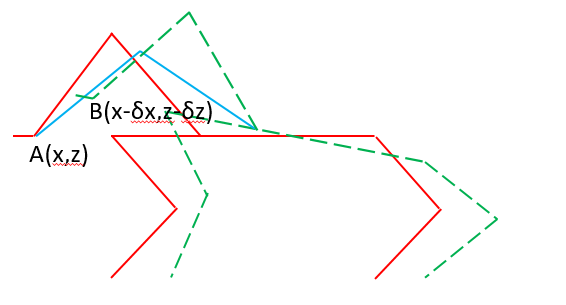 从上面两幅图可以总结出,我们需要获得到机器人在三个方向上的位移dx、dy和dz,以及yaw和pitch的偏转角度α和β(因为我的狗头只有四个自由度,狗头没法在roll方向旋转,所以这里不考虑roll,波士顿的狗头有五个自由度,所以他们可以)。 那么问题就转换到如何获取这五个参数。 # 惯导实现室内定位 我的四足机器人身上只有一个传感器,那就是安装在机器人身体上的MPU6050,假设我将它安装在机器人的几个中心上。 首先我可以很方便地求出yaw、pitch、roll三个欧拉角,关键是如何求出三个位移,也就是如何实现室内定位。 MPU6050里面有三轴加速度,我们可以利用加速度积分,也就是直线运动的公式计算  其中速度也可以由加速度积分得到。 但是加速度中有重力加速度的干扰,所以在使用加速度前要将重力加速度减去。大体思路如下: 1....
上篇文章解决了四足机器人的三轴姿态解析,完成了机器人六个参数中的三个,这篇文章解决剩下三个参数。 # 前进后退 前进后退都是一个道理,这里只谈前进。 四足动物的前进有好几种 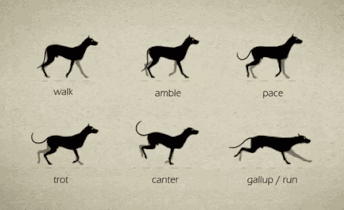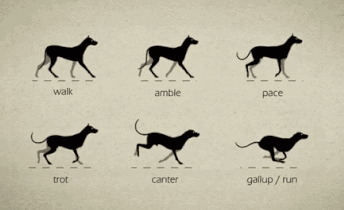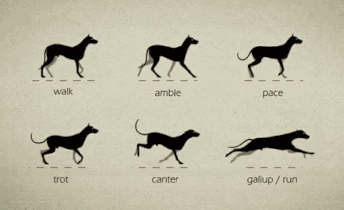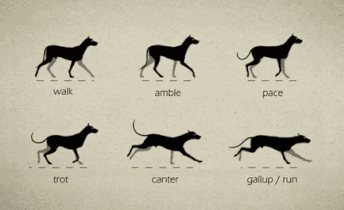 鉴于舵机的性能,估计我也只能完成walk(走)、pace(踱步)和trot(小跑)三个方式。 这里可以参考波士顿的spotMini的表现    这里就以trot为例进行解析,模型如下  * 首先迈出左前和右后腿(第一幅图),然后机器人身体往前移动,直到左前和右后腿又回到初始位置(第二幅图) * 此时迈出右前和左后腿(第三幅图),机器人身体继续向前移动,直到右前和左后腿又回到初始位置(第四幅图) * 此时迈出左前和右后腿(第一幅图),然后重复上述步骤,实现机器人前进。 实现起来很简单,只要周期性地改变每条腿的位置就行了。 # 左右平移 看看spotMini表现得怎么样  这个也可以分解为一个循环,这里以左移为例  * 首先迈出左前和右后腿(第一幅图),然后机器人身体向左移动,直到左前和右后腿又回到初始位置(第二幅图) * 此时迈出右前和左后腿(第三幅图),机器人身体继续向左移动,直到右前和左后腿又回到初始位置(第四幅图)...
不久前我捣鼓过如果从GitHub page使用JavaScript访问其他仓库的源代码([原文在此](https://imuncle.github.io/content.html?id=55)),当时我是想用来加载非`username.github.io`下的HTML文件才搞了这么一出,当时处理js文件时还挺麻烦的。 不过今天我发现一个更方便地方法,直接访问https://htmlpreview.github.io/  或者访问 ```javascript https://htmlpreview.github.io/?https://github.com/twbs/bootstrap/blob/gh-pages/2.3.2/index.html ``` 上面的问号后面是要访问的资源地址 还拿上次那个示例,之前的访问地址是https://imuncle.github.io/example.html?repo=Funny&path=Flappy&doc=index.html 现在可以访问https://htmlpreview.github.io/?https://github.com/imuncle/Funny/blob/master/Flappy/index.html 什么问题都处理的妥妥的。 不过我之前那个方法也不是没用了,它还可以用来动态加载一些资源,会灵活很多。
常用的单片机与PC端通信的方式是使用一些USB转TTL的芯片,比如CH430等,这种方法比较麻烦,还要额外买模块,而且受波特率限制,但是使用STM32自带的USB功能就不怕这些了。 # USB CDC简介 *该部分摘录自[USB CDC从理论到实践](https://blog.csdn.net/king_jie0210/article/details/76713938)* USB CDC属于USB 2.0标准下的一个子类,定义了通信相关设备的抽象集合。   USB CDC类的通信部分主要包含三部分:枚举过程、虚拟串口操作和数据通信。其中虚拟串口操作部分并不一定强制需要,因为若跳过这些虚拟串口的操作,实际上USB依然是可以通信的,这也就是为什么上图中,在操作虚拟串口之前会有两条数据通信的数据。 之所以会有虚拟串口操作,主要是我们通常使用PC作为Host端,在PC端使用一个串口工具来与其进行通信,PC端的对应驱动将其虚拟成一个普通串口,这样一来,可以方便PC端软件通过操作串口的方式来与其进行通信,但实际上,Host端与Device端物理上是通过USB总线来进行通信的,与串口没有关系,这一虚拟化过程,起决定性作用的是对应驱动,包含如何将每一条具体的虚拟串口操作对应到实际上的USB操作。 需要注意的是,**Host端与Device端的USB通信速率并不受所谓的串口波特率影响**,它就是标准的USB2.0全速(12Mbps)速度,实际速率取决于总线的实际使用率、驱动访问USB外设有效速率(两边)以及外部环境对通信本身造成的干扰率等因素组成。 # USB CDC基础功能的实现 最基础的功能当然是消息的收发了。首先是STM32CubeMX的配置: ## STM32CubeMX配置 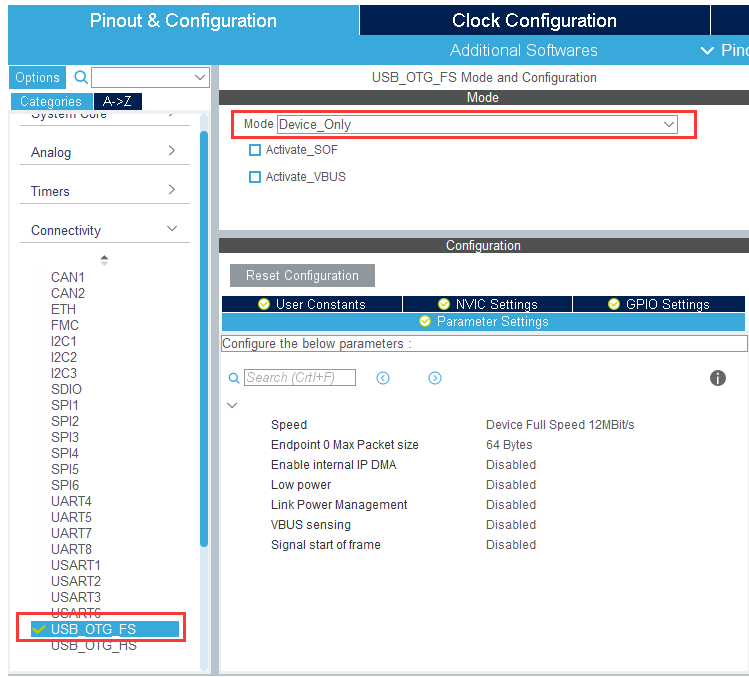 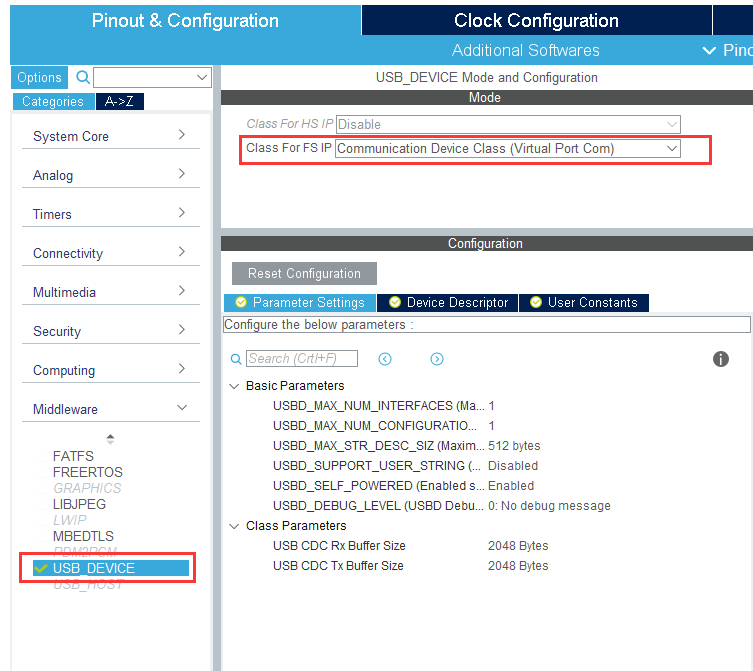 ## 实现代码 点击生成代码后,会有以下几个文件生成: 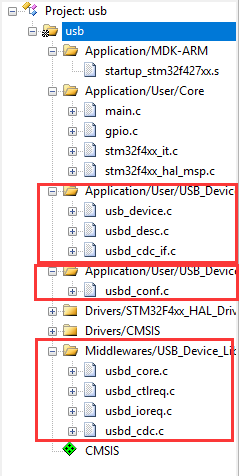 我们只需要关心`usbd_cdc_if.c`文件,可以从这个文件中发现下面的代码: ```c USBD_CDC_ItfTypeDef...
前段时间搞裁判系统的时候接收过浮点数的数据,今天捣鼓超级电容的时候想到,可以把电容的电压反馈给主控板,这其中就会涉及到串口发送浮点数的问题。 由于浮点数本身存储方式与整形数据存储方式有很大不同,感兴趣的可以看这篇博客([32位单精度浮点数表示法](https://blog.csdn.net/liubing8609/article/details/78844121)),总之就是比较复杂,所以浮点数的发送我使用指针而不是按位发送。 定义的结构体如下: ```c struct { uint8_t header; float cap_v; uint8_t end; } tx_data; ``` 发送部分如下: ```c tx_data.header = 0xFF; tx_data.end = 0xFE; tx_data.cap_v = 3.1415f; HAL_UART_Transmit(&huart1, (uint8_t *)&tx_data, sizeof(tx_data),...
文章转自:[理解javascript中的立即执行函数(function(){})()](https://www.cnblogs.com/yanzp/p/6371292.html) 写的很好,在此转载记录一下。 --- 之前看了好多代码,都有用到这种函数的写法,但是都没认真的去想为什么会这样写,今天开始想学习下jquery的源码,发现jquery也是使用这种方式,用`(function(window, undefined){})(window)`包裹内部代码,于是进一步的去学习了下。 要理解立即执行函数`(function(){})()`,先了解些函数的基本概念(函数声明、函数表达式、匿名函数)。 ## 函数声明 使用function声明函数,并指定函数名。 ```javascript function setFn() { // coding } ``` ## 函数表达式 使用function声明函数,但未指定函数名,将匿名函数赋予一个变量。 ```javascript var setFn = function() { // coding } ```...
在GitHub上找到一个有趣的项目[FlappyLearning](https://github.com/xviniette/FlappyLearning),在线demo地址在[这里](https://xviniette.github.io/FlappyLearning/)。 前段时间正好我看了一些机器学习方面的教程,顿时起了兴趣,下载下来读了源码。 首先说,JavaScript语言是不适合搞机器学习和神经网络的,因为它对矩阵运算支持非常差,基本就靠for循环运算矩阵了。换言之,用js写出来的小程序肯定复杂不到哪去,正适合我这种初学者入门。 昨天我把这个项目的游戏部分剥离了出来,可以点这里[试玩](https://imuncle.github.io/example.html?repo=Funny&path=Flappy&doc=index.html),使用鼠标或手指点击控制小鸟煽动翅膀。 今天则研究了一下它的神经网络部分。 首先还是简单介绍一下什么是神经网络。 # 神经元 神经网络是模仿人脑的神经系统设计出来的,神经网络由很多神经元组成。典型的神经元的样子如下:  上面的神经元有三个输入(input)和一个输出(output),每一个输入有一个权重(weight),三者关系如下: `output = input1 * weight1 + input2 * weight2 + input3 * weight3` # 神经网络 神经网络就是由数个神经元组合起来的一个大整体:  其中,最左侧一列的神经元是输入层,最右侧一列是输出层,剩下中间的是隐藏层。可以看出,隐藏层越多,每一层神经元数目越多,整个系统就更复杂,就能实现更加复杂的功能。 #...
