Beam search not always better Greedy search
@patrickvonplaten
I was recently tinkering around the generation strategies for a decoder, and came across this blog post on decoding methods. It was quite useful to clarify how generation works for transformers. Thank you for this excellent work. I notice that in the section on Beam Search, it is stated that:
Beam search will always find an output sequence with higher probability than greedy search, but is not guaranteed to find the most likely output.
It seems to me that the highlighted part is not true, which can illustrated by the following, extended from the example in your blog post.
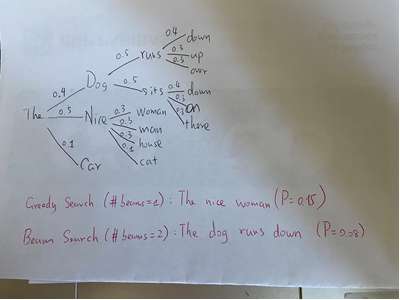
Basically if better beams at a certain time are followed by more tokens in which the preference of tokens is not that strong (distribution being flatter), then the greedy result could have a higher probability, and being missed out by the beam search. I got curious about this claim, because I tried beam search and greedy search in a vision encoder decoder model (Donut), and got lower probability generations quite often with beam search.
What do you think? Is there something else that I over-looked in this example?
Thank you and have a nice day.
The => Dog => runs => down is 4 levels deep, while The => Nice => women is 3 levels deep. I suppose all trees must have the same depth to work out a counter-example. I am not sure if such an exmaple is truely not possible, but just that this one is not that.
Suki
On Wed, Mar 29, 2023 at 6:47 PM Jiali Mei @.***> wrote:
@patrickvonplaten https://github.com/patrickvonplaten
I was recently tinkering around the generation strategies for a decoder, and came across this blog post https://huggingface.co/blog/how-to-generate on decoding methods. It was quite useful to clarify how generation works for transformers. Thank you for this excellent work. I notice that in the section on Beam Search, it is stated that:
Beam search will always find an output sequence with higher probability than greedy search, but is not guaranteed to find the most likely output.
It seems to me that the highlighted part is not true, which can illustrated by the following, extended from the example in your blog post.
[image: image] https://user-images.githubusercontent.com/3142085/228549175-d37bb8af-ed62-44bf-93f8-38d22bf6aba3.png
Basically if better beams at a certain time are followed by more tokens in which the preference of tokens is not that strong (distribution being flatter), then the greedy result could have a higher probability, and being missed out by the beam search. I got curious about this claim, because I tried beam search and greedy search in a vision encoder decoder model (Donut), and got lower probability generations quite often with beam search.
What do you think? Is there something else that I over-looked in this example?
Thank you and have a nice day.
— Reply to this email directly, view it on GitHub https://github.com/huggingface/blog/issues/977, or unsubscribe https://github.com/notifications/unsubscribe-auth/AAI67K6ZJ3UPIAGIUN2LRJTW6QY6JANCNFSM6AAAAAAWL63RUQ . You are receiving this because you are subscribed to this thread.Message ID: @.***>
Hi @Sukii From what I understand, whether it's in beam search or in greedy search, the sentence is finished when the end of sequence token is reached. The length of the generated sequence is part of the generation result, and does not prohibit us from comparing the probability of these two sequences.
And in any case, if after the token "woman", you have two possibilities, for ex sits (0.8), and stands (0.2), you will have the results
beam search (number of beams = 2): P = 0.08 for The => Dog => runs => down
and
grid search (number of beams = 1): P = 0.12 for The => nice => woman => sits
Yes, but I suppose the end token is also a token with some probability, so in a sense the tree keeps going any way. These trees in reality have too many branches (as the exact zero valued probability is an extreme rarity). BTW: I could be wrong, as I am no expert in this topic.
Suki
On Thu, Mar 30, 2023 at 5:02 PM Jiali Mei @.***> wrote:
Hi @Sukii https://github.com/Sukii From what I understand, whether it's in beam search or in greedy search, the sentence is finished when the end of sequence token is reached. The length of the generated sequence does not prohibit us from comparing the probability of these two sequences.
— Reply to this email directly, view it on GitHub https://github.com/huggingface/blog/issues/977#issuecomment-1490142564, or unsubscribe https://github.com/notifications/unsubscribe-auth/AAI67K66SLWRLKFAAN455CTW6VVLHANCNFSM6AAAAAAWL63RUQ . You are receiving this because you were mentioned.Message ID: @.***>
Also I thought that beam search with num_beams=3 also includes num_beams < 3. I do not know if that is always the case, like you say even if there is an end token appearing in the middle. If it is the case that teh end_token can cause break, as you say in some such model generation, then is it a bug?
Suki
On Thu, Mar 30, 2023 at 5:42 PM Suki Venkat @.***> wrote:
Yes, but I suppose the end token is also a token with some probability, so in a sense the tree keeps going any way. These trees in reality have too many branches (as the exact zero valued probability is an extreme rarity). BTW: I could be wrong, as I am no expert in this topic.
Suki
On Thu, Mar 30, 2023 at 5:02 PM Jiali Mei @.***> wrote:
Hi @Sukii https://github.com/Sukii From what I understand, whether it's in beam search or in greedy search, the sentence is finished when the end of sequence token is reached. The length of the generated sequence does not prohibit us from comparing the probability of these two sequences.
— Reply to this email directly, view it on GitHub https://github.com/huggingface/blog/issues/977#issuecomment-1490142564, or unsubscribe https://github.com/notifications/unsubscribe-auth/AAI67K66SLWRLKFAAN455CTW6VVLHANCNFSM6AAAAAAWL63RUQ . You are receiving this because you were mentioned.Message ID: @.***>
Very cool conversation here! Yes indeed beam search can lead to more tokens being generated which may have lower overall probs.
So I guess the statement:
Beam search will always find an output sequence with higher probability than greedy search, but is not guaranteed to find the most likely output.
only holds true when all generations have the same number of tokens.
Note to counteract the differences in length, we have the length penalty parameter: https://huggingface.co/docs/transformers/v4.27.2/en/main_classes/text_generation#transformers.GenerationConfig.length_penalty
Very cool conversation here! Yes indeed beam search can lead to more tokens being generated which may have lower overall probs.
So I guess the statement:
Beam search will always find an output sequence with higher probability than greedy search, but is not guaranteed to find the most likely output.
only holds true when all generations have the same number of tokens.
Actually, following the discussion above with @Sukii , it now looks like the statement can even be false when the two methods yield sequences of the same length, as illustrated by the following modified example.
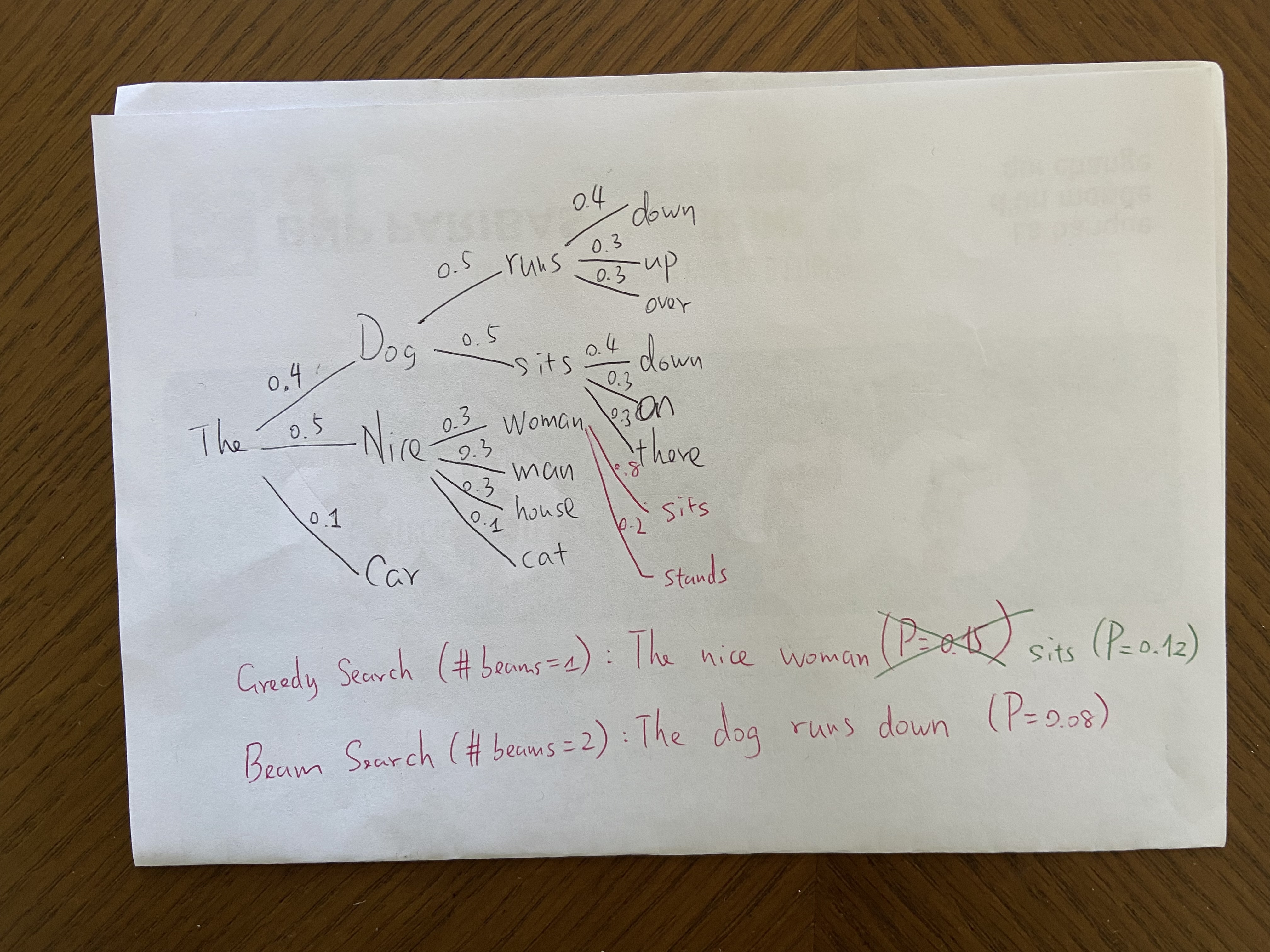
It seems unclear to me if beam search is truly that much better than simple greedy search.
Also a relative newcomer to this, but as I understand it, beam search reduces to greedy search for the first beam up to the max length. So as long as your max length is >=4 in this example, beam search and greedy search will settle on the same solution. Additional beams will explore other options. If the max length is much shorter than the sequence length, then beam search can select a prefix with a less deterministic path to the end which results in a lower probability.
Very cool conversation here! Yes indeed beam search can lead to more tokens being generated which may have lower overall probs. So I guess the statement:
Beam search will always find an output sequence with higher probability than greedy search, but is not guaranteed to find the most likely output.
only holds true when all generations have the same number of tokens.
Actually, following the discussion above with @Sukii , it now looks like the statement can even be false when the two methods yield sequences of the same length, as illustrated by the following modified example.
It seems unclear to me if beam search is truly that much better than simple greedy search.
This thread seems relevant, supports @vermouthmjl in defying the beam search's claim of being optimally superior. And I find it legitimate too.
But from what I suspect might be the reason for the initial claim though is the assumption that when dealing with in real-world data. I have no reference to back the existence of this assumption, but it is trivially intuitive and is as follows: the conditional probabilities significantly shrink down with increasing sequence length. That is, the conditional probabilities of the nodes at each incremental step of beam search (even for greedy and most other decoding strategies). This is because the probability of a node's occurrence decreases as the the number of nodes that it is conditioned on increases. For example, in NLP, a randomly sampled bi-gram has a higher joint probability than a randomly sampled tri-gram.
In the examples given by @vermouthmjl and the forum thread that I shared, counter examples are found whenever this assumption fails to hold.
Some aspects are domain dependent. In NLP head-parser approach, the subject head is crucial and decides the tail (so greedy search might work), but in dependency parser approach (which is nowadays the preferred approach) the verb is everything (in German were sometimes you have to wait for the speaker to speak the verb before you understand what he is talking about) so you may have to wait and do beam search. So the statement:
"Beam search will always find an output sequence with higher probability than greedy search, but is not guaranteed to find the most likely output."
However, it is understood that very deep parsing is also problematic as you pointed out. Shallow parsing seems the more preferred approach. As Oscar Wilde cleverly put it:
"All art is at once surface and symbol. Those who go beneath the surface do so at their peril. Those who read the symbol do so at their peril."