Numerical derivative of a time dependent function defined by two arrays

[jleman]

trafficstars

Is it possible to use ForwardDiff to find the numerical scalar derivative of a time dependent function defined with two arrays? For example:

t=[0 1 2 3 4 5 6 7 8 9] #time array with uniform time step magnitude=[1 4 6 4 3 0 1 2 4 6] #magnitude of the time dependent function at each time step

Something like derivative(magnitude , t)? The output would be an array of the same length as 't' and 'magnitude'.

[briochemc]

ForwardDiff.jl applies to functions. So in your case, you would need to define a function f such that magnitude is equal to f applied to all the values in t, i.e., magnitude = f.(t). Do you have such an f?

(PS: Use backticks "`" for displaying code properly — see GitHub help)

[jleman]

Thank you for the reply. The data cannot be described by an analytical function. I am importing the result from a simulation of torque transients. The result is a function in that there is only one value for each time t and the result is continuous (see image), otherwise it cannot be described with an equation. Thanks for the tip on code snippets.

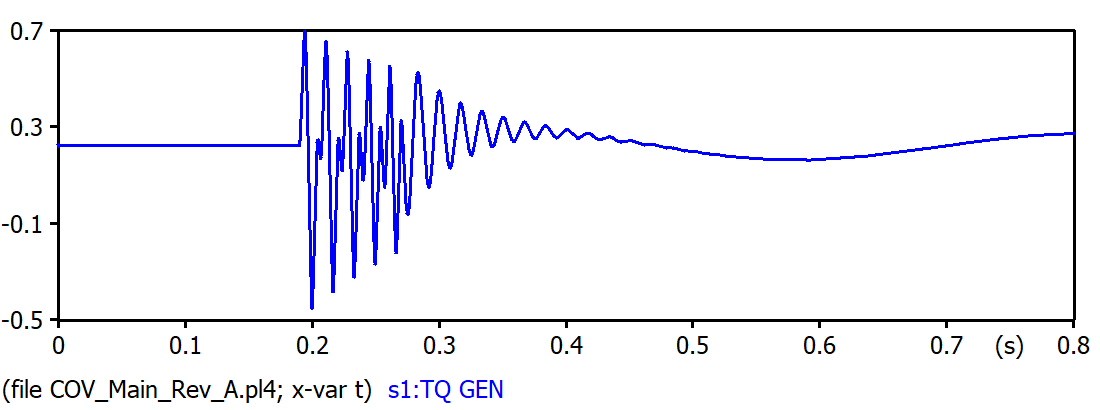
When you say function are you referring to an analytical function that can be described by an equation or would this data qualify? I have a magnitude array and a corresponding time array.

Here is the code I am trying. The last line contains the derivative attempt.

using GR
using DelimitedFiles
using ForwardDiff

data=readdlm("Data.csv",Float64) #read in torque versus time data (2 columns of data)
t=data[:,1]  #store the time data
torque=data[:,2] #store the torque data

nettorque=zeros(length(t)) #initalize an array for storing net torque data
acceleration=zeros(length(t)) #initalize an array for storing acceleration data
velocity=zeros(length(t)) #initialize a velocity array
angle=zeros(length(t)) #initialize an angle array

H=1.2 #intertia constant
S=58.8e6 #total power
wo=1800*2*π/60.0 #angular speed in rad/s
J=2*H*S/wo^2 #moment of inertia

nettorque.=torque.-torque[1] #calculate net torque

acceleration.=nettorque/J #calculate acceleration
velocity=ForwardDiff.derivative(acceleration,t) #take the numerical derivative of the acceleration to find velocity

The result:

MethodError: no method matching derivative(::Array{Float64,1}, ::Array{Float64,1})
Closest candidates are:
  derivative(::Any, ::AbstractArray, !Matched::Real) at C:\Users\JLeman\.julia\packages\ForwardDiff\okZnq\src\derivative.jl:27
  derivative(::Any, ::AbstractArray, !Matched::Real, !Matched::ForwardDiff.DerivativeConfig{T,D} where D) where T at C:\Users\JLeman\.julia\packages\ForwardDiff\okZnq\src\derivative.jl:27
  derivative(::Any, ::AbstractArray, !Matched::Real, !Matched::ForwardDiff.DerivativeConfig{T,D} where D, !Matched::Val{CHK}) where {T, CHK} at C:\Users\JLeman\.julia\packages\ForwardDiff\okZnq\src\derivative.jl:27
  ...

Stacktrace:
 [1] top-level scope at In[6]:22

[briochemc]

You do not need any packages for that, you just need to apply finite differences with your time steps:

velocity = diff(magnitude) ./ diff(t)

[briochemc]

I guess this issue can be closed now?