Make matrix algebra (`zero`,`one`,`*`,`+`, ...) work with special matrix types

[c42f]

The correct general behavior for zero and one is to construct a StaticArrays type which can represent the additive and multiplicative identities. Currently this doesn't always work for the reasons described in JuliaLang/julia#763: for example, zero(Rotations.RotMatrix) should not return a RotMatrix.

One fix would be to make operations always call similar_type and refine the documentation for similar_type to specify that it should return the type of a "general full matrix". "Full" for the purposes of array ops like broadcasting which don't preserve "structural zeros", and full for algebraic purposes because we need a member of GL(n,R) as generic output. This seems consistent(ish?) with similar in Base. Note that changing to use similar_type like this is slightly breaking and led to JuliaLang/julia#700, so this will technically be a breaking change. However we need to do something like this for correctness so we should do it in the next major release. Generally I don't think it will be very breaking...

Perhaps there's some more general option where similar_type can somehow be aware of the algebraic operation... eg, for multiply to call similar_type(m, *, sz, ty)... but I'm not sure that would be any better than simply overriding *.

[andyferris]

Yeah right it's kinda tricky!

What are the properties that you want for zero and one, really? I'm going to take a stab...

1. If T is monoidal under +, such that +(::T, ::T) --> T, then I expect zero(::T) --> T.
2. If T is monoidal under *, such that *(::T, ::T) --> T, then I expect one(::T) --> T.

So a rotation is 2 but not 1. So what is the desired behavior when a concrete type is not monoidal? A weaker condition that still preserves types as much as possible might be this:

1. x + zero(x) --> typeof(x)
2. x * one(x) --> typeof(x).

So in this scenario I wouldn't care exactly what type that zero(x) or one(x) returns so long as it obeys the above. I think it's both too weak and too strong though...

It might be too weak because you could also have one(matrix) = one(eltype(matrix)). I think there might be some generic guarantees you want like one(::Number) --> Number and one(::AbstractMatrix) --> AbstractMatrix. I guess if we define both scalar * matrix and matrix * matrix then there is both the "scalar identity" and the "matrix identity"?

That condition above might be too strong though because the only way I can see to make this work for all AbstractMatrix types would be to have ZeroArray and OneMatrix, I suppose carrying around their (possibly static) sizes. (So for rotations you could have +(::Rotation, ::ZeroMatrix) --> Rotation).

So I dunno what the "right" thing could be?? Mathematics says a lot about sets (i.e. instances of types) and operations (i.e. functions like +, *) and categorizing these into magmas, fields, vector spaces, etc... but I haven't come a lot across operetors that aren't closed and talk about different sets, like you get with Julia promotion +(::T1, ::T2) --> T3 and the kinds of difficulties here.

[andyferris]

PS Hacker News just referred to this: https://jwkennington.com/blog/algebra-ladder/

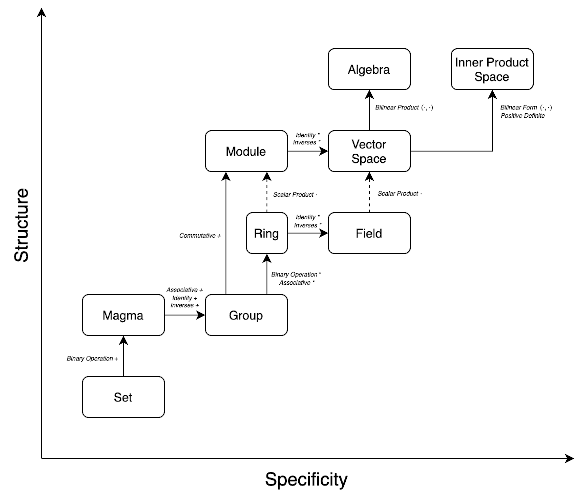
I think something similar for Julia but with the arrows being properties implemented in generic functions like +, *, zero and one, would be cool. I believe Haskell does things somewhat this way. (You always run into trouble with floating point arithmetic being not-quite associative, though...)

[andyferris]

Maybe the best we can hope for is this?

1. If T is monoidal under +, such that +(::T, ::T) --> T, then I expect zero(::T) --> T.
2. In any case, we require x + zero(x) == zero(x) + x == x.
3. If T is monoidal under *, such that *(::T, ::T) --> T, then I expect one(::T) --> T.
4. In any case, we require x * one(x) == one(x) * x == x.

(One might argue about == vs isequal, etc).

That covers zero(::AbstractArray) returning an AbstractArray of the right size... I wonder if we need the distributive law or something to make sure one(::AbstractMatrix) returns an array not a scalar? How about:

5. one(x) + zero(x) == one(x).

That might do it. (Similarly I'd expect one(x) * zero(x) == zero(x) to work).

The rest of the type details are likely implementation details/performance hacks - and not algebraic necessities required to write generic algorithms at a higher level.

[c42f]

Beautiful summary, thanks. Those algebraic properties seem about right.

In mathematics there's some precedent for expanding the set of things which operators act on into a union of several unrelated-seeming sets to achieve closure. The multivectors of exterior / geometric algebra feel like that kind of thing when you first see them. Also I was surprised in the same kind of way by Fock space in QM having states of different number.

Coming back to Earth, what about something like ZeroArray{Axs,T,N} <: AbstractArray{T,N} and OneMatrix{Axs,T} <: AbstractMatrix{T}? For StaticArrays we could have Axs <: NTuple{N,SOneTo}, but it might generalize beyond StaticArrays. Presumably we would need to at least keep the axes as fields? I worry about lifting too much into the type domain.

Also this should relate to UniformScaling in some way but I'm not quite sure how?

[andyferris]

Right. Well for now I don't think we need ZeroArray or OneMatrix, just so long as what we implement here and in Rotations obeys some obvious rules that won't leave people surprised we should be golden.

Also this should relate to UniformScaling in some way but I'm not quite sure how?

Good question! I've always been slightly uneasy with it, so maybe. I think I mostly want scalar addition (matrix + 1 meaning matrix + I) and eye(), and not I at all, but I'm probably the odd one out!

[c42f]

just so long as what we implement here and in Rotations obeys some obvious rules

Sure, agreed. From that point of view we can just use similar_type, document that it should return a type able to hold a full matrix, and document that one and zero should be implemented by people who want them for their special matrix types.

[tkf]

If you start considering T = Union{UniformScaling,CustomArray} or T = Union{Number,CustomArray} as a monoid things start being fishy. As a consequence, we have

julia> diagm(ones(3)) == I == diagm(ones(4))
true

Though I guess this is kind of OK because T in the comment above is not really a type. It's more like a subset T of all possible values of type T′ with the same size. That is to say, diagm(ones(3)) and diagm(ones(4)) won't be in the same set T and you are dealing with the equivalence class defined by == rather than the Julia objects themselves.

---

BTW, do you guys know that

julia> isequal(diagm(ones(3)), I)
true

julia> isequal(diagm(ones(4)), I)
true

julia> hash(I)
0x6bd2535d045989b2

julia> hash(diagm(ones(4)))
0x6ba2635b5ca237d8

julia> hash(diagm(ones(3)))
0xf728e5a95d43274d

? I couldn't find anything in Julia's issue tracker so I think I'll post it there.

[andyferris]

Yeah that isequal thing seems wrong to me. == is probably OK?

For the record, my monoidal comments referred to concrete types T only (these days I'm more interested in the value domain; what I really mean is *(x, x) isa typeof(x) should imply that one(x) isa typeof(x) - which is what you want for a generic algorithm to be type stable and fast and users not to be surprised by output types, which is a common complaint around here btw...).

[tkf]

For the record, my monoidal comments referred to concrete types T only

Ah, maybe I generalized your comment too much. Maybe you are only talking about T <: StaticArray? I was thinking that T may be Matrix{Float64} (a subset of Matrix{Float64} can be a monoid with * or + but Matrix{Float64} itself is not).

(I posted the issue on isequal here: https://github.com/JuliaLang/julia/issues/35485)

[c42f]

Should we be trying to address this in some practical way for version 1.0?

It's easy to revert #763 to make one() work "better".

But things get subtle when trying to work out what similar is really meant to do (and by extension similar_type), so I'm tempted to punt on documenting the precise expected behavior of similar_type.

For example, LinearAlgebra thinks that similar for triangular matrices should preserve the triangular structure rather than returning a general matrix:

        # For A<:AbstractTriangular, similar(A[, neweltype]) should yield a matrix with the same
        # triangular type and underlying storage type as A. The following method covers these cases.
        similar(A::$t, ::Type{T}) where {T} = $t(similar(parent(A), T))
        # On the other hand, similar(A, [neweltype,] shape...) should yield a matrix of the underlying
        # storage type of A (not wrapped in a triangular type). The following method covers these cases.
        similar(A::$t, ::Type{T}, dims::Dims{N}) where {T,N} = similar(parent(A), T, dims)

[lxvm]

Hi, I ran into this issue when trying to apply one(A) to an array A with units. For this case, I would expect one(A) == oneunit(A)/oneunit(eltype(A)), however I see the following error (using Julia v1.9.2, StaticArrays v1.6.2, and Unitful v1.16.2)

julia> using Unitful

julia> x = 1.0u"m"
1.0 m

julia> one(x)
1.0

julia> using StaticArrays

julia> A = one(SMatrix{2,2})*u"m"
2×2 SMatrix{2, 2, Quantity{Float64, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}, 4} with indices SOneTo(2)×SOneTo(2):
 1.0 m  0.0 m
 0.0 m  1.0 m

julia> one(A)
ERROR: DimensionError: m and 1.0 are not dimensionally compatible.
Stacktrace:
 [1] convert(#unused#::Type{Quantity{Float64, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}}, x::Float64)
   @ Unitful ~/.julia/packages/Unitful/QEYHc/src/conversion.jl:112
 [2] macro expansion
   @ ~/.julia/packages/StaticArraysCore/U2Z1K/src/StaticArraysCore.jl:81 [inlined]
 [3] convert_ntuple
   @ ~/.julia/packages/StaticArraysCore/U2Z1K/src/StaticArraysCore.jl:77 [inlined]
 [4] SMatrix{2, 2, Quantity{Float64, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}, 4}(x::NTuple{4, Float64})
   @ StaticArraysCore ~/.julia/packages/StaticArraysCore/U2Z1K/src/StaticArraysCore.jl:113
 [5] _construct_sametype
   @ ~/.julia/packages/StaticArrays/J9itA/src/linalg.jl:99 [inlined]
 [6] _one(s::Size{(2, 2)}, m_or_SM::SMatrix{2, 2, Quantity{Float64, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}, 4})
   @ StaticArrays ~/.julia/packages/StaticArrays/J9itA/src/linalg.jl:108
 [7] one(m::SMatrix{2, 2, Quantity{Float64, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}, 4})
   @ StaticArrays ~/.julia/packages/StaticArrays/J9itA/src/linalg.jl:101
 [8] top-level scope
   @ REPL[30]:1

I would be open to reverting #763 and making a PR in Rotations.jl to fix the behavior, if this would be helpful.