Finding the optimal displayable area

[BingyaoHuang]

trafficstars

Welcome to discuss more efficient algorithms.

For a mask image imMask below , the optimal displayable area (i.e., the largest inscribed rectangle) can be found by rect = getLargestRect(imMask, aspectRatio); where aspectRatio is the aspect ratio of the inscribed rectangle, and it should match your projector input images/frames aspect ratio.

• When aspect ratio = 1, rect = getLargestRect(imMask, 1);

• When aspect ratio = 4/3, rect = getLargestRect(imMask, 4/3);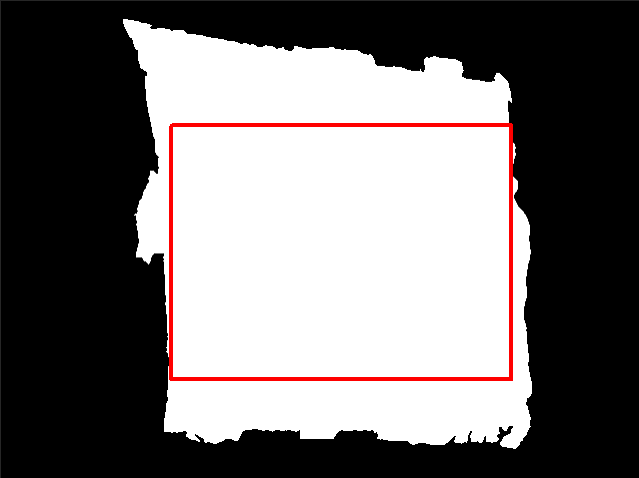

Function getLargestRect is an iterative rectangle growing algorithm written in MATLAB 2021a, and is defined below:

%% find the largest inscribed rectangle of a binary image imBW.
function [rect] = getLargestRect(imBW, aspectRatio)
% aspectRatio is the aspect ratio of the inscribed rect (w/h)
h = size(imBW, 1);
w = size(imBW, 2);

% find candidate rect centers using distance transform
imDist = bwdist(~imBW);
[cy, cx] = find(imDist > prctile(imDist(imBW), 90)); % to speedup, only select the inner 90% points as candidate rect centers

% only use a subset for speedup (fix RNG seed to be deterministic)
seed = RandStream('mlfg6331_64');
idx = randsample(seed, length(cx), min(200, length(cx)));
cx = cx(idx);
cy = cy(idx);

% max size of the inscribed rect
maxH = 0;
% maxW = 0;

% for each candidate center
for i = 1: length(cy)
    % left, right x and top and bottom y
    lx = cx(i);
    rx = cx(i);
    ty = cy(i);
    by = cy(i);
    
    % iteratively grow the current inscribed renctangle toward top-left and bottom-right by 1 pix
    while(1)
        % move the top-left corner toward top-left by 1 pix
        curH = by - ty + 1;
        dx = round(curH * aspectRatio) - round((curH - 1) * aspectRatio);
        
        if(ty - 1 >= 1 && lx - dx >= 1)
            imRect = imBW(ty-1:by, lx-dx:rx);
            if(nnz(~imRect(:)) == 0)
                ty = ty - 1;
                lx = lx - dx;
            else
                break;
            end
        else
            break;
        end
        
        % move the bottom-right corner toward bottom-right by 1 pix
        curH = by - ty + 1;
        dx = round(curH * aspectRatio) - round((curH - 1) * aspectRatio);
        
        if(by + 1 <= h && rx + dx <= w)
            imRect = imBW(ty:by+1, lx:rx+dx);
            if(nnz(~imRect(:)) == 0)
                by = by + 1;
                rx = rx + dx;
            else
                break;
            end
        else
            break;
        end
    end
    
    % record the centers with the largest inscribed rectangle
    curH = by - ty + 1;
    if(curH > maxH)
        maxH = curH;
        bestx = cx(i);
        besty = cy(i);
        bestRect = [lx, ty, rx-lx+1, by-ty+1];
    elseif(curH == maxH)
        bestx = [bestx, cx(i)];
        besty = [besty, cy(i)];
        bestRect = [bestRect; [lx, ty, rx-lx+1, by-ty+1]];
    end
end

% finally, find the best rect whose center has the largest distance
[~, idx] = max(imDist(sub2ind(size(imDist), besty, bestx)));
rect = bestRect(idx, :);
figure; imshow(imBW); rectangle('Position', rect, 'EdgeColor','r', 'LineWidth', 3); drawnow
end

[ynd316]

When I used the code as it was, there was an issue that I could not get the same result as the image above the this page. However, in my case, the same result could be obtained by changing line 9 [cy, cx] = find(imDist > prctile(imDist(imBW), 90)); to [cy, cx] = find(imDist > prctile(imDist, 90));

Matlab 2021b version was used, and ad-on installed only Statistics and Machine Learning Toolbox, Image Processing Toolbox, and Computer Vision Toolbox.

[BingyaoHuang]

Thank you for the feedback. Maybe it's due to the MATLAB version. Note that this modification may not work well in other versions, and it produces a suboptimal result in MATLAB 2021a.